图形算法：圆形生成算法

图形算法：圆形生成算法

标签（空格分隔）： 算法

版本：2
作者：陈小默
声明：禁止商用，禁止转载

发布于：作业部落、CSDN博客

---

圆的定义为所有距离中心位置$(x_c,y_c)$为定值 $r$ 的点的集合1。在本章内容中，我们将会介绍三种常用的圆形生成算法：勾股定理算法、极坐标算法和中点圆算法。

一、算法导论

---

1.1 四分法与八分法

由于圆具有对称性，只计算圆上一部分的值，再通过对称性将值变换到其他象限可以极大的减少计算量。

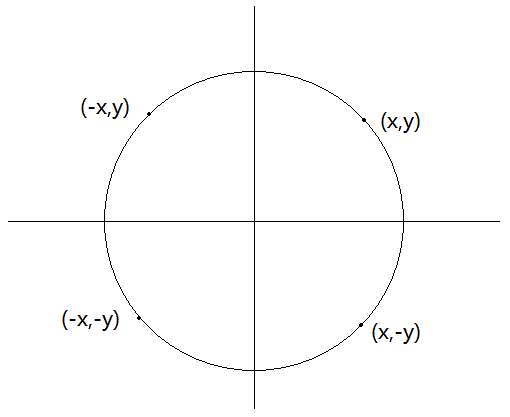
假如我们确定了圆在第一象限的位置，则可以通过变换 $y$ 的符号去生成圆在第二象限的位置。我们再对上述生成的全部位置进行相对于 $x$ 轴的符号变换就可以得到圆在第三四象限的位置。这就是四分法的基本思路。

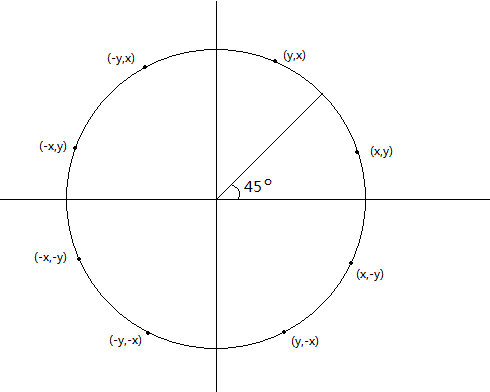
在同一个象限内，如果按照 $45^o$ 进行分割，可以看出其坐标关于这个分割线是对称的。也就是在(0~45)度范围内的值可以通过简单变换映射到其他区域内。这种分割方式被称为圆的八分法。

1.2 勾股定理算法

在笛卡尔坐标系中，对于给定的原点$(x_c,y_c)$和半径 $r$，圆上任意一点$(x,y)$满足勾股定理

$$(x-x_c)^2+(y-y_c)^2=r^2 \tag{1.2.1}$$

利用这个算法我们可以通过任意 $x$ 值计算对应的 $y$ 值

$$y=y_c \pm \sqrt{r^2-(x_c-x)^2} \tag{1.2.2}$$

现在我们通过示例程序演示该算法，仅展示思路，可使用任意语言或图形软件包实现。

void Pythagorean(int x,int y,int r){//使用勾股定理绘制圆
        int start = x-r;
        int end = r+x;
        _IntArray _arr;
        int size = 4*(end-start);
        _arr = new IntArray(size);
        IntArray_ arr = *_arr;
        int r2 = r*r;
        for(int i=start,j=0;i<end;i++){
            int p = sqrt(float(r2-power(x-i)));
            arr[j++]=i;
            arr[j++]=y+p;
            arr[j++]=i;
            arr[j++]=y-p;
        }
        _list->add(_arr);
    }

通过结果 [图 1.2-1] 我们可以看出直接使用勾股定理会造成像素间距不一致的问题。处理方法有两种：第一种是在斜率的绝对值大于1后，交换$x$和$y$来调整间距；第二种方式是使用1.1节中提到的八分法。我们只需要计算八分之一的图形，剩下的操作就是简单映射即可。以下是使用八分法的示例

void Pythagorean(int xc,int yc,int r){//使用勾股定理和八分法绘制圆
        int len = int(1+0.5*sqrt(2.0)*r);
        int size = 16*len;
        _IntArray _arr = new IntArray(size);
        IntArray_ arr = *_arr;
        int r2 = r*r;
        int j=0;
        for(int x=0;x<len;x++){
            int p = sqrt(float(r2-power(x)));
            arr[j++]=x;
            arr[j++]=p;
        }
        int k=j;
        for(int i=0;i<k;i+=2){
            arr[j++] = arr[i+1];
            arr[j++] = arr[i];
        }
        k = j;
        for(int i=0;i<k;i+=2){
            arr[j++] = arr[i];
            arr[j++] = -arr[i+1];
        }
        k = j;
        for(int i=0;i<k;i+=2){
            arr[j++] = -arr[i];
            arr[j++] = arr[i+1];
        }
        for(int i=0;i<j;i+=2){
            arr[i]+=xc;
            arr[i+1]+=yc;
        }
        _list->add(_arr);
    }

在此示例中，我们先将圆计算时的圆心已原点(0，0)计算，在所有操作完成之后在平移到相应位置，这么做方便变换简化计算量。

总结：勾股定理算法简单，即使是使用八分法缩减运算规模，其大量复杂的开平方计算仍然是影响效率的关键因素。接下来，我们将介绍一种能够替换开平方运算的算法。

1.3 极坐标算法

极坐标系是一种常用的坐标系。其中坐标位置由到原点的极半径距离 $r$ 和距水平轴的角 $\theta$ 指定。正的角位移是逆时针的，而负的角位移是逆时针的。利用三角函数的定义，可以从极坐标系转换为笛卡尔坐标系。

$$x=r cos\theta , y = r sin\theta \tag{1.3.1}$$

通过式(1.3.1)我们可以通过下列方程组表示圆方程

$$x=x_c+r cos\theta \tag{1.3.2}$$

$$y=y_c+r sin\theta \tag{1.3.3}$$

使用上述方式以单位角度为步长，可以在圆周上以等距离的点来绘制圆。

下面将使用程序展示极坐标算法的计算过程

    void Polar(int xc,int yc,int r){//使用极坐标系绘制圆
        int point = 2;//每一度绘制两个点
        double angle = 1.0/point;//每两个点之间的角度
        int size = point*45*8*2;//使用八分法，
        _IntArray _arr = new IntArray(size);
        IntArray_ arr = *_arr;
        int j=0;
        for(int i=0;i<45;i++){
            for(int m=0;m<point;m++){
                arr[j++] = int(r*cos(((i+angle*m)*(PI/180))));//使用c库中的三角函数需要将角度转换为弧度
                arr[j++] = int(r*sin(((i+angle*m)*(PI/180))));
            }
        }
        int k=j;
        for(int i=0;i<k;i+=2){
            arr[j++] = arr[i+1];
            arr[j++] = arr[i];
        }
        k = j;
        for(int i=0;i<k;i+=2){
            arr[j++] = arr[i];
            arr[j++] = -arr[i+1];
        }
        k = j;
        for(int i=0;i<k;i+=2){
            arr[j++] = -arr[i];
            arr[j++] = arr[i+1];
        }
        for(int i=0;i<j;i+=2){
            arr[i]+=xc;
            arr[i+1]+=yc;
        }
        _list->add(_arr);
    }

总结：我们可以从图中看出其边缘有毛刺状突起，这是因为极坐标系运算以角度为步长而不是任何一个轴，这就导致其结果取整后不仅仅只会在一个方向上浮动。从效率的角度上说，虽然极坐标系统提供了等距离点，但是其三角函数计算仍然十分耗时。

1.4 中点圆算法

我们可以参照直线算法中的Bresenham算法，以决策参数的增量运算为基础，将圆的计算过程转换为简单的整数加减运算。

如同画线算法，我们在每一步中以单位间隔取样并确定离圆最近的像素位置。对于给定半径 $r$ 和屏幕中心 $(x_c,y_c)$ ，可以现将圆的圆心放在坐标原点运算，在运算完成之后，再将圆移动到相应的位置。

为了应用中点圆算法，我们先定义一个圆函数

$$f_{circ}(x,y) = x^2+y^2-r^2 \tag{1.4.1}$$

任意一点 $(x,y)$ 均满足

$$f(n) = \begin{cases} \lt 0, & \text{(x,y)在圆周边界之内} \\ =0, & \text{(x,y)在圆周边界之上} \\ \gt 0, & \text{(x,y)在圆周边界之外} \end{cases} \tag{1.4.2}$$

我们需要使用(1.4.2)对每一个取样步上对接近圆周的两个像素的中点进行测试。因此，在中点算法中，圆函数(1.4.1)是决策参数。

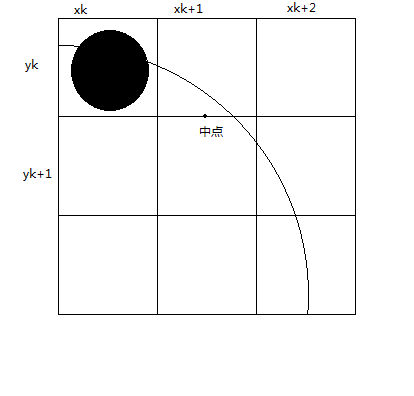
图 [1.4-1] 给出了取样位置 $x_k+1$ 上的中点，我们可以取出中点的坐标 $(x_k+1,(y_k+y_k-1)/2)$ 也就是点$(x_k+1,y_k-\frac{1}{2})$ ，接下来，我们只需要将中点位置代入方程(1.4.1)就可以算出决策参数

$$p_k=f_{circ}(x_k+1,y_k-\frac{1}{2}) \\ =(x_k+1)^2+(y_k-\frac{1}{2})^2-r^2 \tag{1.4.3}$$

如果$p_k \lt 0$，那么这个圆的轨迹在中点的上方，所以我们选择扫描 $y_k$ 这个像素，否则，我们扫描$y_k-1$这个像素。

接下来我们要寻找决策增量之间的关系。这使用了我们中学所学的数学归纳法。通过任意相邻两点之间的关系递推整个决策的关系。

通过式(1.4.4)我们可以求出下一个决策参数

$$p_{k=1}=f_{circ}(x_{k+1}+1,y_{k+1}-\frac{1}{2}) \\ =[(x_k+1)+1]^2+(y_{k+1}-\frac{1}{2})^2-r^2 \tag{1.4.4}$$

我们可以找出相邻的两个决策参数之间的关系

$$p_{k+1}=p_k+2(x_k+2)+(y_k-y_{k+1}) \tag{1.4.5}$$

其中 $y_{k+1}$ 是 $y_k$ 或者是 $y_k-1$ 具体取值取决于 $p_k$ 的符号。

我们已经计算出了决策增量的关系，接下来只需要计算出决策增量的初始值即可，对于圆心在坐标原点，半径为 $r$ 的圆来说，假设第一点从$(0,r)$处起笔

$$p_0 = f_{circ}(1,r-\frac{1}{2}) \\ = 1+(r-\frac{1}{2})^2-r^2 \\ = \frac{5}{4}-r \tag{1.4.6}$$

如果为了简化运算，我们可以将决策参数近似为整数，而不用浮点数，其中 $r$ 也是整数

$$p_0 = 1-r \tag{1.4.7}$$

接下来我们将使用一段代码来解释其流程：

    void Bresenham(int xc,int yc,int r){//使用中点圆算法
        int j = 0;
        int p = 1-r;//这里计算出的p0使用近似的整型来简化运算
        int x = 0;
        int y = r;
        int size = 16*int(1+0.5*sqrt(2.0)*r);//整个运算过程会产生size/2个点
        _IntArray _arr = new IntArray(size);
        IntArray_ arr = *_arr;
        for(int i=x;i<y;i++){
            arr[j++] = x++;
            if(p<0){//决策参数小于0说明中点在圆内，所以点要绘制在上方
                arr[j++] = y;
                p+=2*x+1;
            }else{
                arr[j++] = y--;
                p+=2*x+1-2*y;
            }
        }
        int k=j;
        for(int i=0;i<k;i+=2){
            arr[j++] = arr[i+1];
            arr[j++] = arr[i];
        }
        k = j;
        for(int i=0;i<k;i+=2){
            arr[j++] = arr[i];
            arr[j++] = -arr[i+1];
        }
        k = j;
        for(int i=0;i<k;i+=2){
            arr[j++] = -arr[i];
            arr[j++] = arr[i+1];
        }
        for(int i=0;i<j;i+=2){
            arr[i]+=xc;
            arr[i+1]+=yc;
        }
        _list->add(_arr);
    }

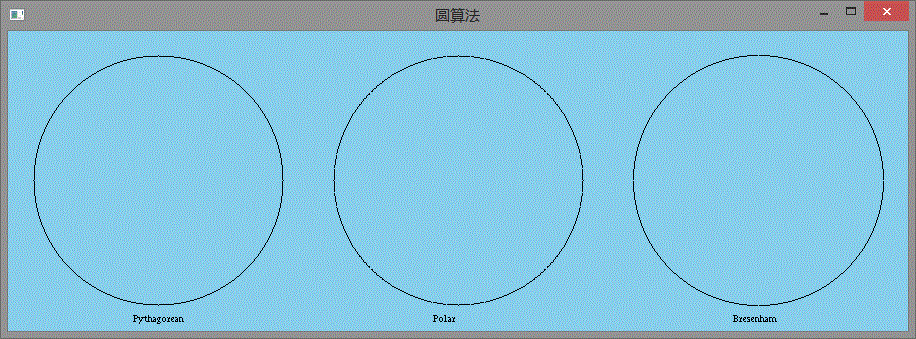
图中示例分别为勾股定理(左)，极坐标系(中)和中点算法(右)

---

1. 计算机图形学第四版.电子工业出版社.109~114 ↩