【BZOJ4574】【Zjoi2016】线段树 dp

UPD：妈蛋一觉醒来被吓到了。。。小透明诚惶诚恐的把代码滚去注释了一番。。。

辣鸡卡常题。。。30s的题bzoj上30124ms跑出来。。。

好嘛我承认我只是把某位神犇的博客的代码抄了一遍，这里是传送门

下面是就着AC代码逆向yy题解的时间

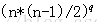
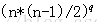
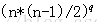
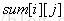
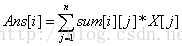
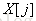
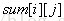
首先题目要求是每个位置的期望乘以的值，那么其实就是让我们求出在所有个操作序列下，第i个位置的种可能值的和再取模。我们注意到当操作完之后，第i个位置的值一定是最开始给定的n个数值之一，那么我们可以原序列排序并且离散成1~n（不用并且不推荐去重因为没有影响），设表示序列的第i个位置在所有q次操作后变成了（离散后的）j 的方案的数量数。那么答案就可以表示为

，其中表示在原来的序列中排第j的元素（就是把离散的序列映射回去）。于是问题转化为如何统计。

个人感觉这个统计方法和寿司晚宴有异曲同工之妙（其实并没有）。。。

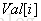
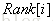
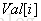
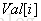
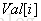
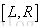
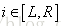
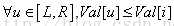
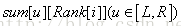
我们设表示未排序的原序列的第i个元素值，表示这个元素的名次，考虑这个值对周围的一个区域有贡献（即在q次操作以后，周围存在一个区域的值变成了），这个区域的极限就是从这个元素向左向右延伸从未碰到某个元素比他大，因为一旦包含了一个比大的元素，将不在对这个局域有贡献。更形式化一点，对于每个i，存在一个区间，满足并且。在这个区域内我们计算。

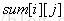
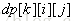
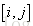
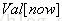
为了方便计算，我们将的含义改成序列的第i个位置在所有q次操作后小于等于（离散后的）j 的方案数（最终处理答案之前再减回来）。我们设now是当前正在计算的元素，表示k次操作之后，使得这一段的任意一个元素都小于等于的方案的数量之和 ，边界为

转移状态为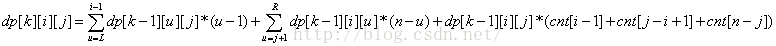（我相信你萌看到这个是方的，请仔细体会）

其中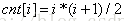，意义为从一个长度为i的序列中选取一个子序列的方案数。

处理出dp以后，利用公式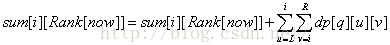处理出sum数组即可（这里的sum的意义是小于等于）。

处理完n个位置以后再对sum相减求和既是答案。

不得不说ZJ的题确实妖孽。。。

UPD:有关状态转移方程的前两项我自己也是连蒙带猜。。。不难发现从k-1转移到k的时候，一个状态只会转移到他的某个子集，因为只能选择一个区间，所以只有两种转移到【真】子集的方法，分别叫做“左边固定从右边缩进来”、“右边固定从左边缩进来”，系数则表示从缩的点出发，向左（右）可延伸的长度。

而自己转移到自己的时候，可以从i的左边任选一个区间(cnt[i-1]),或者右边任选一个(cnt[n-j]),或者中间任选一个(cnt[j-i+1])，都不会出问题。

/**************************************************************
    Problem: 4574
    User: RicardoWang
    Language: C++
    Result: Accepted
    Time:30124 ms
    Memory:5880 kb
****************************************************************/
 
#include<cstdlib>
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
#define maxn 410
#define mo 1000000007
int n,q,x[maxn],y[maxn],rank[maxn];
int cnt[maxn],A[maxn][maxn];long long dp[2][maxn][maxn],sum[maxn][maxn];
bool mycmp(int a,int b)
{
  return x[a]<x[b];
}
void Init()//读入并排序
{
  scanf("%d%d",&n,&q);
  for(int i=1;i<=n;i++)scanf("%d",&x[i]);//x[i]装原数组
  for(int i=1;i<=n;i++)y[i]=i;//第i小的元素是y[i]
  sort(y+1,y+1+n,mycmp);
  for(int i=1;i<=n;i++)rank[y[i]]=i;//元素i是第rank[i]小的
  return ;
}
#define dp(i,j,k) dp[(i)%2][j][k]//滚动数组优化空间
void solve(int l,int r,int now)
{
  for(int i=l;i<=r;i++) for(int j=l;j<=r;j++)dp(0,i,j)=dp(1,i,j)=0;
  dp(0,l,r)=1;
  long long ct;
  for(int k=1;k<=q;k++)
  {
    for(int i=l;i<=r;i++)
    {
      ct=0;
      for(int j=r;j>=i;j--)
      {
        dp(k,i,j)=ct; ct=(ct+dp(k-1,i,j)*(n-j))%mo;//计算第二项
      }
    }
    for(int j=l;j<=r;j++)
    {
      ct=0;
      for(int i=l;i<=j;i++)
      {
        dp(k,i,j)=(dp(k,i,j)+ct)%mo; ct=(ct+dp(k-1,i,j)*(i-1));//计算第一项
      }
    }
    for(int i=l;i<=r;i++)
    {
      for(int j=i;j<=r;j++)
      {
        dp(k,i,j)=(dp(k,i,j)+(dp(k-1,i,j)*A[i][j]))%mo;//计算第三项
      }
    }
  }
  for(int i=l;i<=r;i++)
  {
    ct=0;
    for(int j=r;j>=i;j--)
    {
      ct=(ct+dp(q,i,j));//加入到sum数组
      sum[j][rank[now]]=(ct+sum[j][rank[now]])%mo;
    }
  }
  return ;
}
int main()
{
  //freopen("in.txt","r" ,stdin);
 // freopen("out.txt","w",stdout);
  Init();
  int l,r;
  for(int i=1;i<=n;i++)  cnt[i]=i*(i+1)/2;//从一个长度为i的序列中选取一个子序列的方案数。
  for(int i=1;i<=n;i++)for(int j=i;j<=n;j++)A[i][j]=cnt[i-1]+cnt[n-j]+cnt[j-i+1];//这一步其实可以不要
  memset(sum,0,sizeof(sum));
  for(int i=1;i<=n;i++)
  {
    l=r=i;
    while(l && x[l]<=x[i])l--; while(r<=n && x[r]<=x[i])r++;//计算每个元素可能有贡献的区域
    solve(l+1,r-1,i);
  }
 
  int ans;
  for(int i=1;i<=n;i++)
  {
    ans=0;
    for(int j=1;j<=n;j++)
    {
      if(!sum[i][j])continue;
      for(int u=1;u<j;u++)sum[i][j]=(sum[i][j]-sum[i][u])%mo;//从“小于等于j的元素”变成“刚好等于j的元素”
      ans=((long long)ans+1ll*x[y[j]]*sum[i][j])%mo;
    }
    ans=(ans+mo)%mo;
    if(i!=n) printf("%d ",ans);else printf("%d",ans);
  }
  
  return 0;
}