浅谈线段树

最新推荐文章于 2020-08-02 16:27:00 发布

置顶 Simon_Bariona

最新推荐文章于 2020-08-02 16:27:00 发布

阅读量790

点赞数 3

分类专栏：线段树总结题目文章标签：二叉树线段树递归

本文链接：https://blog.csdn.net/qq_39809664/article/details/78167068

版权

总结同时被 3 个专栏收录

37 篇文章 0 订阅

订阅专栏

题目

8 篇文章 0 订阅

订阅专栏

线段树

3 篇文章 0 订阅

订阅专栏

线段树

线段树

简介:

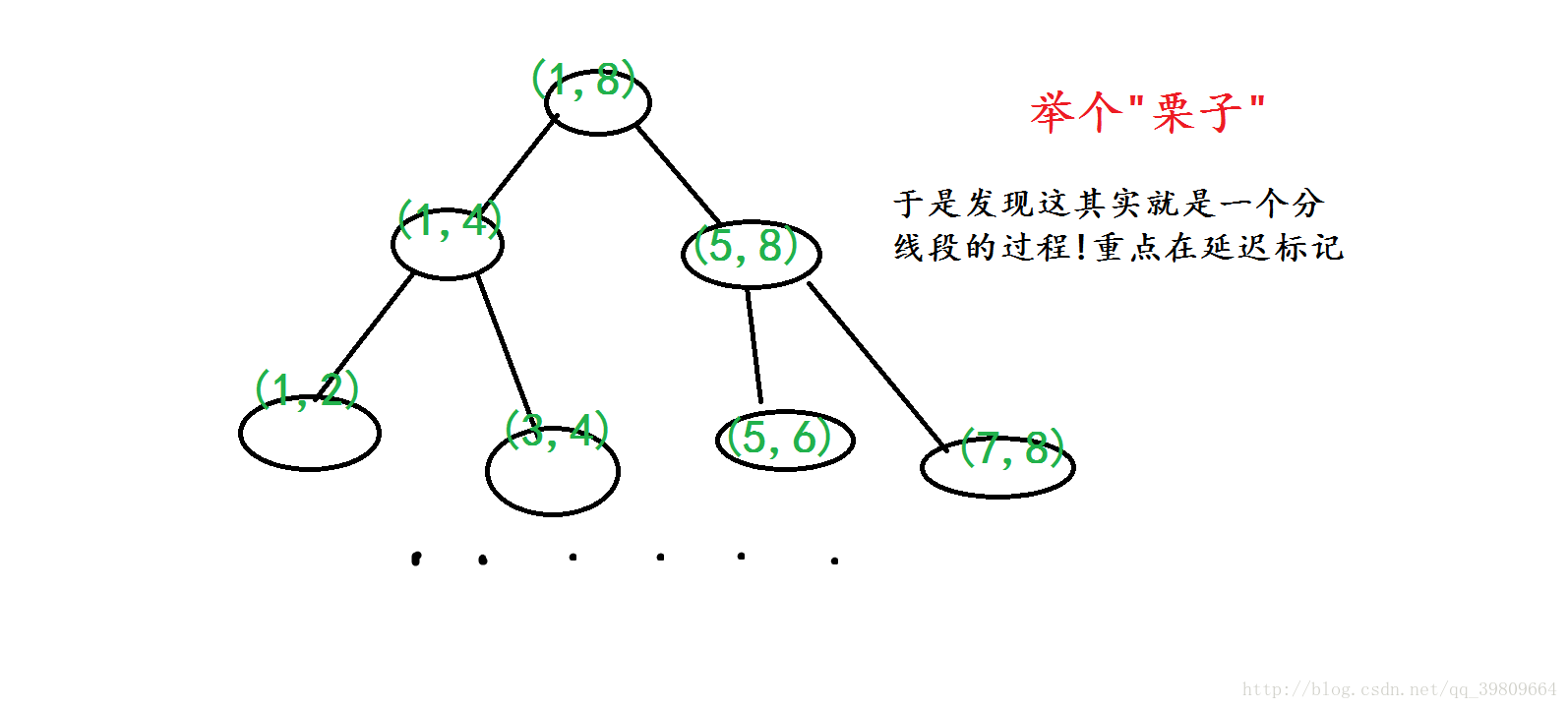
就是将一颗完全二叉树,每个节点存储的是一个节点区间[l,r]之中的值(比如最小值,最大和,总和……)最后在可以在简短的时间复杂度之下实现修改区间,查询区间的功能!

总的来说,就是:先递归,再操作;先传输,再递归!

它在各个节点保存一条线段（数组中的一段子数组），主要用于高效解决连续区间的动态查询问题，由于二叉结构的特性，它基本能保持每个操作的复杂度为O(logn)。

线段树的每个节点表示一个区间，子节点则分别表示父节点的左右半区间，例如父亲的区间是[a,b]，那么(c=(a+b)/2)左儿子的区间是[a,c]，右儿子的区间是[c+1,b]。
十分的强大!

初始化:

这里写图片描述

单节点初始化:

主要注意的就是这里是对于一个区间进行二分的操作
那么就是注意是肯定是要先进行 build 之后在进行分开的计算
不然就会 G_G!!

void build(int now,int start,int end,int a[])
{
    if(start==end)
        t[now].minvalue=a[start];
    else
    {
        int mid=(start+end)/2;
        build( now<<1,start,mid,a ); // 先递归完成了之后,再计算!
        build( now<<1|1,mid+1,end,a );
        t[now].minvalue=min(t[now<<1].minvalue,t[now<<1|1].minvalue);
    }
}

区间修改初始化:

这里的Addmark就是指区间加的值,这里的值就是初始化成为 0 就好了!
之后的用法就会利用到叫一个延迟标记的东东!

void build(int now,int start,int end,int a[])
{
    segTree[now].Addmark=0;
    if(start==end)
        segTree[now].tot=a[start],segTree[now].size=1;
    else
    {

        int mid=(start+end)/2;
        build( now*2  ,start,mid,a );
        build( now*2+1,mid+1,end,a );

        segTree[now].tot=segTree[now<<1].tot+segTree[now<<1|1].tot;
        segTree[now].size=segTree[now<<1].size+segTree[now<<1|1].size;
    }
}

询问的函数

这里写图片描述

单节点询问:

传进来的参数有 qstart 与 qend 表示要询问的区间
而 start 与 end 指的是现在搜到的区间
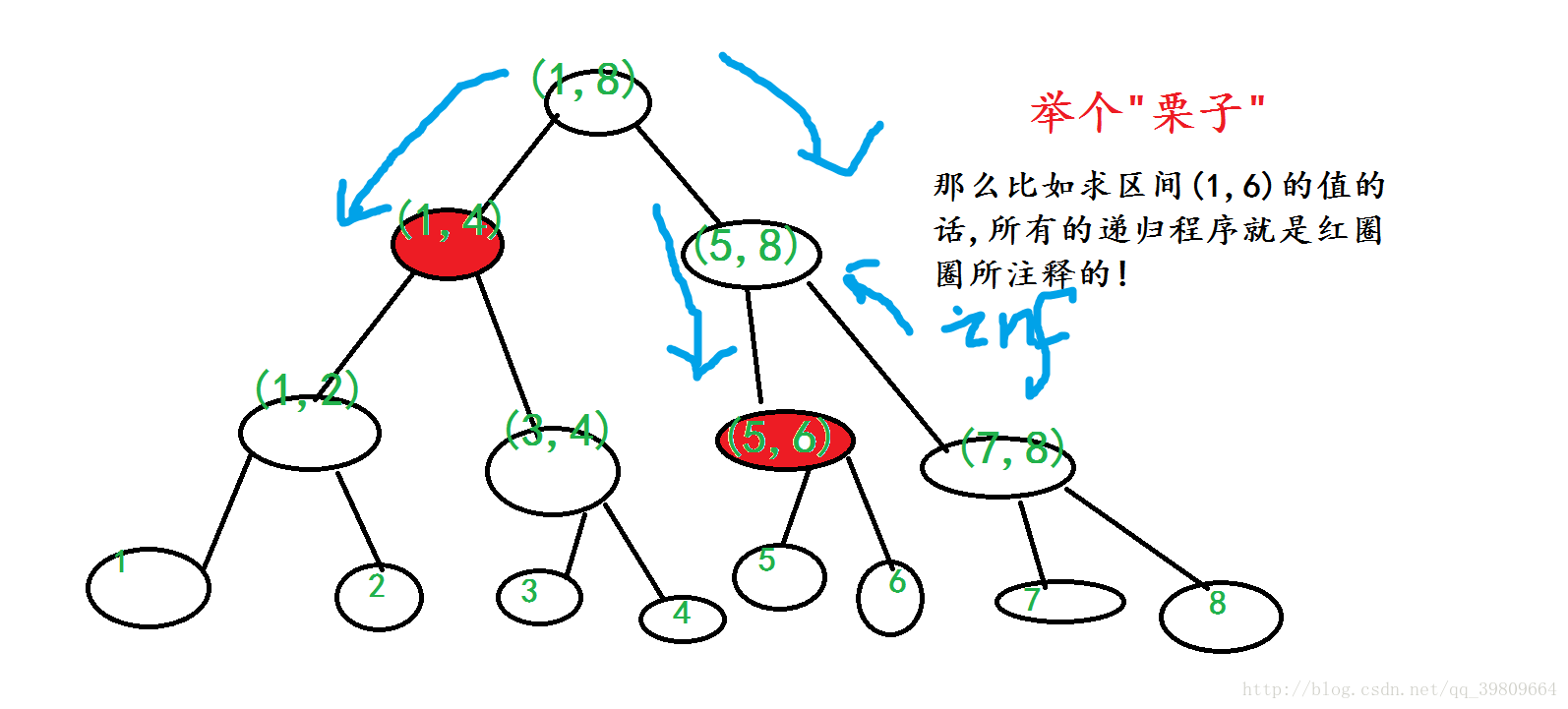
如果现在的 start~end 的区间的值能够被qstart ~qend给包括那么既可以直接返回值了!因为如果继续二分下去 , 所求的值还是能够被大的值给包括!!
但是如果区间真的是完完全全的不重合了,那么我们也没有必要搜索了,因为是求最小值,所以直接返回INF!

int question(int root,int qstart,int qend,int start,int end)
{
    if(start>qend||end<start)
        return inf;
    if(qstart<=start&&qend>=end)
        return t[root].minvalue;
    int mid=(start+end)/2;
    return min(question(root<<1,qstart,qend,start,mid),
               question(root<<1|1,qstart,qend,mid+1,end));

}

区间询问:

那么区间询问同理!
其实这个Addmark 可以想象成为就是一个 “路障” 我们在向下询问的是后就会带上这个标记,也就是区间需要修改!!
只要是在被答案所寻求的区间里面包括了,那么就可以直接反回了!

long long question(int root,int qstart,int qend,int start,int end)
{
    if(start>qend||end<qstart)
        return 0;
    if(qstart<=start&&qend>=end)
        return segTree[root].tot;

    PushDown(root);
    int mid=(start+end)/2;
    return question(root<<1,qstart,qend,start,mid)+question(root<<1|1,qstart,qend,mid+1,end);

}

修改区间(单节点):

单点:

注: change 表示要修改的点的值
这里就是相当与就是递归到了最底层,在找到change之后对其惊醒修改,而别的并不惊醒修改,为什么,因为并不影响其结果!
但是注意了!,需要递归回来
为什么?
因为子节点的变化有可能会引起father节点及其以上的变化!所以在操作完了之后,要对子节点进行修改!!!

void update(int root,int change,int start,int end,int add)
{
    if(start==end)
    {
        if(start==change)
            t[root].minvalue+=add;
        return ;
    }
    int mid=(start+end)/2;
    if(change<=mid)
        update(root<<1,change,start,mid,add);
    else
        update(root<<1|1,change,mid+1,end,add);
    t[root].minvalue=min(t[root<<1].minvalue,t[root<<1|1].minvalue);
}

区间:

区间的一个Addmark 就是对于一个操作,PushDown 就是单纯的将其mark的信息传给它的子节点,为什么只需要这样呢,因为在update的操作里面,已经出现的递归程序,所以这样就相当于是连贯了起来,相当于形象来说就是代代相传!!(就是爷爷传给父亲,再是父亲穿给自己)

因为我们在下放延迟标记的时候,只是会将需要的时候,也就是搜索到的时候才会将延迟标记下放,但是我们如果不用到的话,那么子节点就是暂时是不需要动的,因为,者可以相当于是一个父子关系

比如,有什么困难,先是父亲先来解决,但是如果他解决不了了,那么才需要孩子了出面解决!但是,两个人所携带的信息是一模一样的!

比如父亲此时有战斗值为 5 ,孩子是 2
但是孩子有延迟标记,之后才会加上比如 1
但是如果父亲能够解决,在直接叫父亲,但是实在不行,就要先Pushdown (father) 把father 的信息传下来!再叫孩子上!
但是先要叫孩子的武力值加上 2 ,就是变成了 4 ,再来解决问题,不行再来,在来….(但是每一次都会看看父亲是不是可以!)

void PushDown(int root)
{
    if(segTree[root].Addmark!=0)
    {
        segTree[root<<1].Addmark+=segTree[root].Addmark;
        segTree[root<<1|1].Addmark+=segTree[root].Addmark;

        segTree[root<<1].tot+=segTree[root<<1].size*segTree[root].Addmark;
        segTree[root<<1|1].tot+=segTree[root<<1|1].size*segTree[root].Addmark;
        segTree[root].Addmark=0;
    }
}
void update(int root,int qstart,int qend,int start,int end,int add)
{
    if(start>qend||end<qstart)
        return ;
    if(qstart<=start&&qend>=end)
    {
        segTree[root].Addmark+=add;
        segTree[root].tot+=add*segTree[root].size;
        return ;
    }
    PushDown(root);

    int mid = ( start + end) / 2;
    update(root<<1, qstart, qend, start, mid, add);
    update(root<<1|1, qstart, qend, mid+1, end, add);
    //=====还是先递归完了之后,在进行操作=====
    segTree[root].tot =segTree[root<<1].tot+segTree[root<<1|1].tot;
}

注释:

所以整个线段树最难的应该就是在这里了!
单点的操作我就不讲了!关键是在区间操作的* 延迟修改*
就单单拿一个区间 (x,y) 加上 k 的一个简单的例子来说吧!
对于一个在线的操作 ,那么对于每一次都操作一遍是不是太麻烦了?所以我们想出来一个办法,在只需要询问的时候讲它输出来操作,别的时候就只需要用数字来记录一下就好了!

Addmark!!!
表示的就是 t[i].Addmark就是这个数字一会需要的操作的加上的值!

再来一个 Push的一个函数! 表示将它的father节点的Addmark的状态与其子节点相加,因为father节点就会包括子节点的嘛!
还有一个小疑问就是为什么是 “+=” 因为可能有一些子节点的状态在之后会被释放或者是father节点有变化,所以就要是+=表示只是将其状态的变化承接下来!
因为在函数PushDown 之中有一个归 0 的东东!

segTree[root].Addmark=0;

就是为了防止之后再一次询问的时候还会再算一遍 ,比如 Addmark =9; 算了之后这个区间就加上了9 ,但是之后如果又来了再加上5 ,不变的话就是加上了 14 ,但是事实上不是的,所以就是加上 5就好了,所以是记得归 0 !

完整代码:

单点

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <cstring>
#include <math.h>
#include <vector>
using namespace std;
const int N=2005;
const int inf=99999999;
int n,val[N];
struct edgytree
{
    int minvalue;
} t[N];
void build(int now,int start,int end,int a[])
{
    if(start==end)
        t[now].minvalue=a[start];
    else
    {
        int mid=(start+end)/2;
        build( now<<1,start,mid,a );
        build( now<<1|1,mid+1,end,a );
        t[now].minvalue=min(t[now<<1].minvalue,t[now<<1|1].minvalue);
    }
}
int question(int root,int qstart,int qend,int start,int end)
{
    if(start>qend||end<start)
        return inf;
    if(qstart<=start&&qend>=end)
        return t[root].minvalue;
    int mid=(start+end)/2;
    return min(question(root<<1,qstart,qend,start,mid),
               question(root<<1|1,qstart,qend,mid+1,end));

}
void update(int root,int change,int start,int end,int add)
{
    if(start==end)
    {
        if(start==change)
            t[root].minvalue+=add;
        return ;
    }
    int mid=(start+end)/2;
    if(change<=mid)
        update(root<<1,change,start,mid,add);
    else
        update(root<<1|1,change,mid+1,end,add);
    t[root].minvalue=min(t[root<<1].minvalue,t[root<<1|1].minvalue);
}
int main()
{
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&val[i]);
    }
    build(1,1,n,val);
    //printf("%d\n",t[3].minvalue);
    return 0;
}

区间:

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <cstring>
#include <math.h>
#include <vector>
using namespace std;
const int N=100005;
int n,m,val[N];
// ´æÁË Ò»¸öÊÇÏë¼ÓµÄÖµ , ºÍÇø¼äÀïÃæ×Ü¹²ÓÐÒ»¸ö ÔªËØ 
struct edgytree
{
    long long tot;
    int Addmark,Minusmark,size;
//¿ªÁËÒ»¸öÊý×é ×îºÃÊÇ 4 ±¶´óµÄÊý×é 
} segTree[4*N];
// ³õÊ¼»¯ 
void build(int now,int start,int end,int a[])
{
    //½«Æä±äÎª 0  
    segTree[now].Addmark=0;
    if(start==end)
        segTree[now].tot=a[start],segTree[now].size=1;
    else
    {

        int mid=(start+end)/2;
        build( now*2  ,start,mid,a );
        build( now*2+1,mid+1,end,a );
        segTree[now].tot=segTree[now<<1].tot+segTree[now<<1|1].tot;
        segTree[now].size=segTree[now<<1].size+segTree[now<<1|1].size;
    }
}
void PushDown(int root)
{
    // ÕâÒ»²½ÊÇ ½« root ½ÚµãµÄÁ½¸öº¢×Ó½Úµã´«Èë×Ô¼ºµÄÐÞ¸ÄÖµ 
    if(segTree[root].Addmark!=0)
    {
        segTree[root<<1].Addmark+=segTree[root].Addmark;
        segTree[root<<1|1].Addmark+=segTree[root].Addmark;

        segTree[root<<1].tot+=segTree[root<<1].size*segTree[root].Addmark;
        segTree[root<<1|1].tot+=segTree[root<<1|1].size*segTree[root].Addmark;
        segTree[root].Addmark=0;
    }
}

long long question(int root,int qstart,int qend,int start,int end)
{
    if(start>qend||end<qstart)
        return 0;
    if(qstart<=start&&qend>=end)
        return segTree[root].tot;

    PushDown(root);
    int mid=(start+end)/2;
    return question(root<<1,qstart,qend,start,mid)+question(root<<1|1,qstart,qend,mid+1,end);

}
void update(int root,int qstart,int qend,int start,int end,int add)
{
    if(start>qend||end<qstart)
        return ;
    if(qstart<=start&&qend>=end)
    {
        segTree[root].Addmark+=add;
        segTree[root].tot+=add*segTree[root].size;
        return ;
    }
    //ÏòÏÂ´©²ÎÊý  
    PushDown(root);

    int mid = ( start + end) / 2;
    update(root<<1, qstart, qend, start, mid, add);
    update(root<<1|1, qstart, qend, mid+1, end, add);

    segTree[root].tot =segTree[root<<1].tot+segTree[root<<1|1].tot;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&val[i]);
    }
    build(1,1,n,val);
    for(int i=1; i<=m; i++)
    {
        int x,y,k,loc;
        scanf("%d",&loc);
        if(loc==1)
        {
            scanf("%d%d%d",&x,&y,&k);
            update(1,x,y,1,n,k);
        }
        else
        {
            scanf("%d%d",&x,&y);
            printf("%lld\n",question(1,x,y,1,n));
        }
    }
    return 0;
}

总结:

就是多学,多想!
讲一个线段通过树的方式拆开来!
可以推荐一个网址,如果不懂的话,说不定你们就是不懂!!呵呵!
大佬的线段树

Simon_Bariona

关注

3
点赞
踩
3

收藏

觉得还不错? 一键收藏
2
评论
浅谈线段树

线段树线段树简介初始化单节点修改区间修改区间询问的函数单节点询问区间询问修改区间单节点单点区间注释完整代码单点区间总结简介:就是将一颗完全二叉树,每个节点存储的是一个节点区间[l,r]之中的值(比如最小值,最大和,总和……)最后在可以在简短的时间复杂度之下实现修改区间,查询区间的功能!它在各个节点保存一条线段（数组中的一段子数组），主要用于高效解决连续区间的动态查询问
复制链接

扫一扫