此文章可以使用目录功能哟↑(点击上方[+])
不敢尝试的acmer不是好的acmer,好吧,再一次败给自己...
Problem 1001 sum
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 131072/131072 K (Java/Others)
Problem Description
Input
Output
Output T lines, each line print a YES or NO.
输出T行，每行一个YES或NO。
Sample Input
3 3
1 2 3
5 7
6 6 6 6 6
Sample Output
NO
Problem Idea
解题思路:
【题意】
给定一个数列,问是否存在连续子串的和为m的倍数
【类型】
预处理前缀和
【分析】
所谓预处理前缀和
顾名思义,就是将前i项的和相加对m取模保存至sum[i]
这时,当某两个位置的模数一样时,此区间内所有数之和必定为m的倍数
为什么呢?证明一下
假设sum[i]=sum[j],则
特别的,若某前缀和取模后为0,意味着数列从头到当前位置所有元素之和已为m的倍数
【时间复杂度&&优化】
O(nT)
题目链接→HDU 5776 sum
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-8
#define LL long long
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 5005;
const int inf = 1000000007;
const int mod = 1000000007;
int sum[N];
bool v[M];
int main()
{
int t,n,m,i,s;
scanf("%d",&t);
while(t--)
{
memset(v,false,sizeof(v));
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
{
scanf("%d",&s);
sum[i]=(sum[i-1]+s)%m;
}
for(i=0;i<=n;i++)//从0开始是因为前缀和取模为0出现一次就可认定区间元素之和是m的倍数
{
if(v[sum[i]])
{
puts("YES");
break;
}
v[sum[i]]=true;
}
if(i>n)
puts("NO");
}
return 0;
} Problem 1002 domino
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 131072/131072 K (Java/Others)
Problem Description
Little White plays a game.There are n pieces of dominoes on the table in a row. He can choose a domino which hasn't fall down for at most k times, let it fall to the left or right. When a domino is toppled, it will knock down the erect domino. On the assumption that all of the tiles are fallen in the end, he can set the height of all dominoes, but he wants to minimize the sum of all dominoes height. The height of every domino is an integer and at least 1.
小白在玩一个游戏。桌子上有n张多米诺骨牌排成一列。它有k次机会，每次可以选一个还没有倒的骨牌，向左或者向右推倒。每个骨
牌倒下的时候，若碰到了未倒下的骨牌，可以把它推倒。小白现在可以随意设置骨牌的高度，但是骨牌高度为整数，且至少为1，并且
小白希望在能够推倒所有骨牌的前提下，使所有骨牌高度的和最小。
Input
The first line of input is an integer T ( 1≤T≤10)
There are two lines of each test case.
The first line has two integer n and k, respectively domino number and the number of opportunities.( 2≤k,n≤100000)
The second line has n - 1 integers, the distance of adjacent domino d, 1≤d≤100000
第一行输入一个整数T(1≤T≤10)
每组数据有两行
第一行有两个整数n和k，分别表示骨牌张数和机会次数。(2≤k,n≤100000)
第二行有n-1个整数，分别表示相邻骨牌的距离d，1≤d≤100000
Output
For each testcase, output of a line, the smallest sum of all dominoes height
对于每组数据，输出一行，最小的高度和
Sample Input
4 2
2 3 4
Sample Output
Problem Idea
解题思路:
【题意】
n张多米诺骨牌排成一列,你可以选k张推倒,现给你相邻骨牌之间的距离,问在保证所有骨牌都能推倒的情况下,所有骨牌的高度之和最小为多少
【类型】
排序
【分析】
首先,在只推一次的情况下,骨牌i的高度hi必须满足hi>=di+1(di为骨牌i和骨牌i+1之间的距离)
而每多推一次,其实只能消去一个间距罢了
那为了骨牌高度之和尽可能小,那必定是要消去间距大的
故将间距排序之后,去掉最大的k-1个即可
特别的,当k>=n时,因为至少每个骨牌都可以单独推,所有骨牌高度与间距无关,只需满足题目要求的骨牌高度至少为1即可
需注意,结果可能会爆int
【时间复杂度&&优化】
O(nlogn)
题目链接→HDU 5777 domino
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-8
#define LL long long
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 5005;
const int inf = 1000000007;
const int mod = 1000000007;
int s[N];
int main()
{
int t,n,k,i;
__int64 ans;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&k);
for(i=1;i<n;i++)
scanf("%d",&s[i]);
sort(s+1,s+n);
ans=n;
for(i=1;i<n&&i<=n-k;i++)
ans+=s[i];
printf("%I64d\n",ans);
}
return 0;
}
Problem 1003 abs
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 131072/131072 K (Java/Others)
Problem Description
Given a number x, ask positive integer y≥2, that satisfy the following conditions:
1. The absolute value of y - x is minimal
2. To prime factors decomposition of Y, every element factor appears two times exactly.
给定一个数x，求正整数y≥2，使得满足以下条件：
1.y-x的绝对值最小
2.y的质因数分解式中每个质因数均恰好出现2次。
Input
The first line of input is an integer T ( 1≤T≤50)
For each test case，the single line contains, an integer x ( 1≤x≤10^18)
Output
For each testcase print the absolute value of y - x
对于每组数据，输出一行y-x的最小绝对值
Sample Input
1112
4290
8716
9957
9095
Sample Output
65
67
244
70
Problem Idea
解题思路:
【题意】
给定一个数x,求正整数y≥2,使得满足以下条件:
1.y-x的绝对值最小
2.y的质因数分解式中每个质因数均恰好出现2次.
【类型】
素数表+暴力枚举
【分析】
观察条件2
因为每个质因数恰好出现2次,所以y必定是一个平方数
假设y=z*z
那么z必定是一个由不同质数构成,且每种质数仅有一个的10^9以内的整数
思来想去,貌似没有什么特别优化的做法,那就暴力来一发
对于一个10^9范围内的数,若它在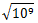
显然,z为质数时也是满足的
那么我们就从sqrt(x)开始,分别向下,向上枚举,直到找到符合题意的z,哪个|y-x|小就取哪个
特判x<4的情况,因为题目规定y>=2
【时间复杂度&&优化】
题目链接→HDU 5778 abs
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-8
#define LL long long
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 50005;
const int M = 5005;
const int inf = 1000000007;
const int mod = 1000000007;
int prime[N],p;
bool v[N];
void get_prime()
{
p=0;
memset(v,false,sizeof(v));
for(int i=2;i<N;i++)
if(!v[i])
{
prime[p++]=i;
for(int j=i+i;j<N;j+=i)
v[j]=true;
}
}
bool judge(__int64 x)
{
int k;
for(int i=0;i<p;i++)
{
k=0;
while(x%prime[i]==0)
{
k++;
x/=prime[i];
if(k>1)
return false;
}
}
return true;
}
int main()
{
get_prime();
int t,j;
__int64 x,k,ans;
scanf("%d",&t);
while(t--)
{
scanf("%I64d",&x);
if(x<4)
{
printf("%I64d\n",4-x);
continue;
}
k=(__int64)sqrt(1.0*x);
for(j=0;;j--)
if(judge(k+j))
break;
ans=abs((k+j)*(k+j)-x);
for(j=1;;j++)
if(judge(k+j))
break;
ans=min(ans,abs((k+j)*(k+j)-x));
printf("%I64d\n",ans);
}
return 0;
}
扫一扫
1069
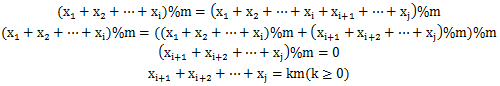
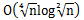
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
