BP神经网络

BP

BP（Back Propagation）网络是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。

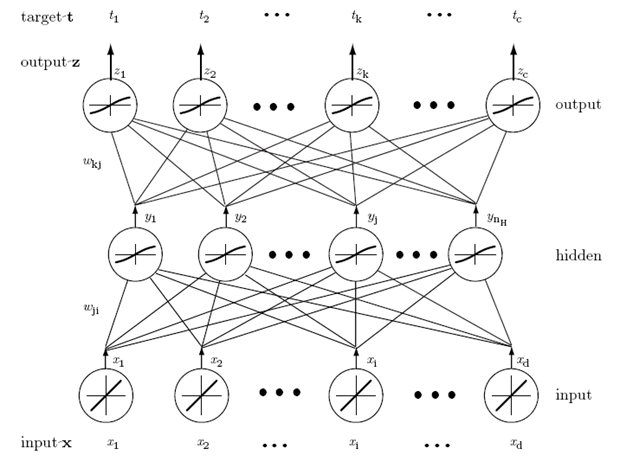
一个神经网络的结构示意图如下所示。

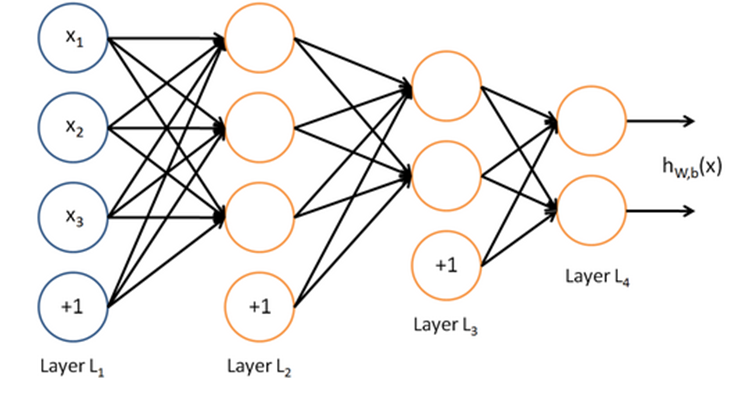
一个四层的神经网络
输入层：三个神经元
隐含层1：三个神经元
隐含层2：两个神经元
输出层：两个神经元

前馈阶段

网络中突触的权值是固定的，输入信号在网络中一层一层的传播，直到输出端。

对某层

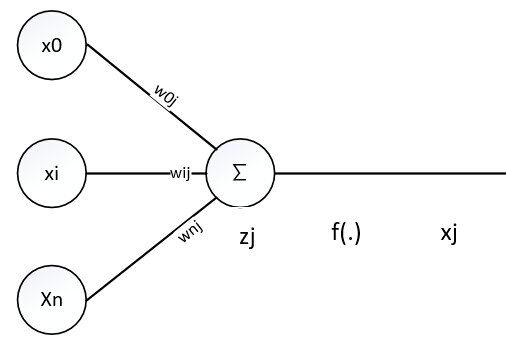
神经元输入结点：

$$x_0,x_1,...,x_i,...x_n$$
其中x0=1 ，w0j可以理解为偏置
第l层神经元结点i到神经元结点j权值是 $$w_{ij}^{l}$$
激活函数一般选：
sigmoid激活函数：
$$f(x) = \frac{1}{1+e^{-x}}$$
值域： $[0,1]$
其导数：
$$f^{'}(x) = f(x)(1-f(x))$$
tanh激活函数：
$$f(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$$
值域： $[-1,1]$
其导数：
$f^{'}(x) = 1-{f(x)}^2$
两个函数的图像：

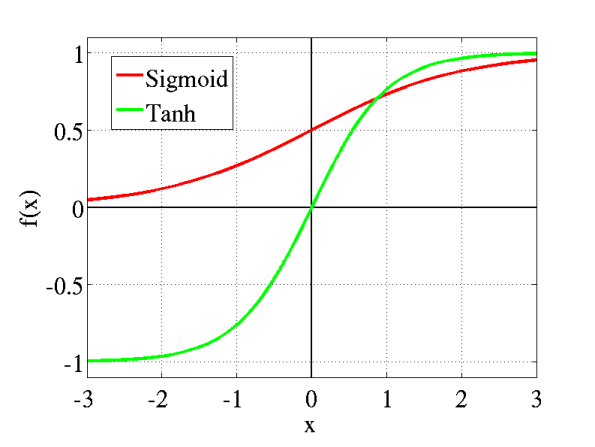
根据上面的一个图，前馈过程就是：
$zj=\sum_{i=0}^{i=n}w_{ij}x_j$
$xj = f(zj)$
这样一层一层的向前递归下去

反馈阶段

反馈阶段是利用训练误差，更新各层神经元权值

先说明下这里反馈阶段更新权值每次是利用一个训练样本数据更新权值

对某一个样本$x$,其各维数据值:${x_0,x_1,x_2,...,x_n}$
设该BP神经网络共有$L$层
第$l$层第i个神经元与第j神经元的权值:$w_{ij}^{(l)}$
第$l$层的神经元数：$S_{l}$,为了方便表示，$S_{l}$从0开始到$S_{l}$结束
第$l$层第i个神经元的加权和:$z^{l}_i$
输出层输出值：$y_0,y_1,...,y_{S_L}$
输出层期望值（也就是该样本数据的真实值）:$d_0,d_1,...,d_{S_L-1}$
对该样本$x$的输出层第j神经元的训练误差：

$$e_j = d_j-y_j$$
对该样本$x$的输出层所有神经元的平方误差:
$$E = \frac{1}{2}\sum_{j=0}^{j=S_L}e_j^2$$
其中：
$y_j = f(z^{(L)}_j)$
$z^{(L)}_j=\sum_{i=0}^{i=S_{L}}w^{(L)}_{ij}x^{(L)}_i$
好的模型应该是输出层神经元的平方误差最小

这里我们需要求的参数只有$w^{l}_{ij}$,下面可以利用梯度下降法或者拟牛顿法进行求解。利用梯度下降法需要计算$E$对$w^{l}_{ij}$的导数，来更新$w^{l}_{ij}$,而拟牛顿法需要计算其二阶导数。
下面利用梯度下降法进行求解

我们知道需要计算$E$对$w^{l}_{ij}$的导数，然而$l$是一个变量，对于$L$层神经网络，其取值范围是$[1,L]$，但是$E$是固定值，是某一个训练样本$x$在输出层各神经元的平方误差。

隐含层到输出层

当$l==L$时，也就是说是隐含层到输出层，需要求的是输出层各神经元的权值矩阵$w^{L}$

网络结构可以简单描述为：

$E$对$w^{L}_{ij}$求导，利用链式法则：

$$\frac{\partial E}{\partial w^{(L)}{ij}} = \frac{\partial E}{\partial e_j}\frac{\partial e_j}{\partial y_j}\frac{\partial y_j}{\partial z^{(L)}_j}\frac{\partial z^{(L)}_j}{\partial w^{(L)}_{ij}}$$
其中：
$\frac{\partial E}{\partial e_j} = e_j$

$\frac{\partial e_j}{\partial y_j}=-1$

$\frac{\partial y_j}{\partial z^{(L)}_j}=f^{'}(z^{(L)}_j)$

$\frac{\partial z^{(L)}_j}{\partial w^{(L)}_{ij}}=x^{(L)}_i$

所以：

$$\frac{\partial E}{\partial w^{(L)}{ij}}=-e_jf^{'}(z_j)x^{(L)}_i$$

在许多论文书籍中往往定义神经元$j$的敏感度
第l层第$j$个神经元的敏感度：

$$\delta^{(l)}_j=-\frac{\partial E}{\partial z^{(l)}_j}$$
也就是，输出层平方误差对神经元j的加权和的偏导数的负数
对输出层 $L$第$j$个神经元的敏感度为:
$$\delta^{(L)}_j=-\frac{\partial E}{\partial z^{(L)}_j}= - \frac{\partial E}{\partial e_j}\frac{\partial e_j}{\partial y_j}\frac{\partial y_j}{\partial z^{(L)}_j}=e_jf^{'}(z_j)=(d_j-y_j)f^{'}(z_j)$$

所以：

$$\frac{\partial E}{\partial w^{(L)}{ij}} = -\delta^{(L)}_j x^{(L)}_i$$
$$\Delta w^{(L)}_{ij}= -\frac{\partial E}{\partial w^{(L)}{ij}}=\delta^{(L)}_j x^{(L)}_i$$
利用梯度下降法更新 $w^{(L)}_{ij}$
$$w^{(L)}_{ij} (n+1)= w^{(L)}_{ij}(n) -\eta \Delta w^{(L)}_{ij}=w^{(L)}_{ij}(n)+\eta \delta^{(L)}_j x^{(L)}_i$$
或者直接写出：

$$w^{(L)}_{ij} (n+1)=w^{(L)}_{ij}(n)+\eta \delta^{(L)}_j x^{(L)}_i$$
其中：
$\eta$是学习率
$\delta^{(L)}_j$是第 $L$层输出神经元$j$的敏感度
$x^{(L)}_i$表示第 $L$层输入神经元$i$的值
$\delta^{(L)}_j=e_jf^{'}(z^{L}_j)=(d_j-y_j)f^{'}(z^{L}_j)$
$n$表示迭代次数

隐含层到隐含层

当$l<=L-1$时，也就是说是隐含层到隐含层，我们需要计算的权值矩阵 $w^{(l)}$在隐含层中， $l$的取值范围从第一层一直到导数第二层，而对该样本$x$的输出层所有神经元的平方误差 $E$是固定的，我们还是用$E$对 $w^{l}_{ij}$求导，但是这个求导过程比较复杂
当 $l=L-1$，这是倒数第二层，其下一层就是输出层
其网络结构：

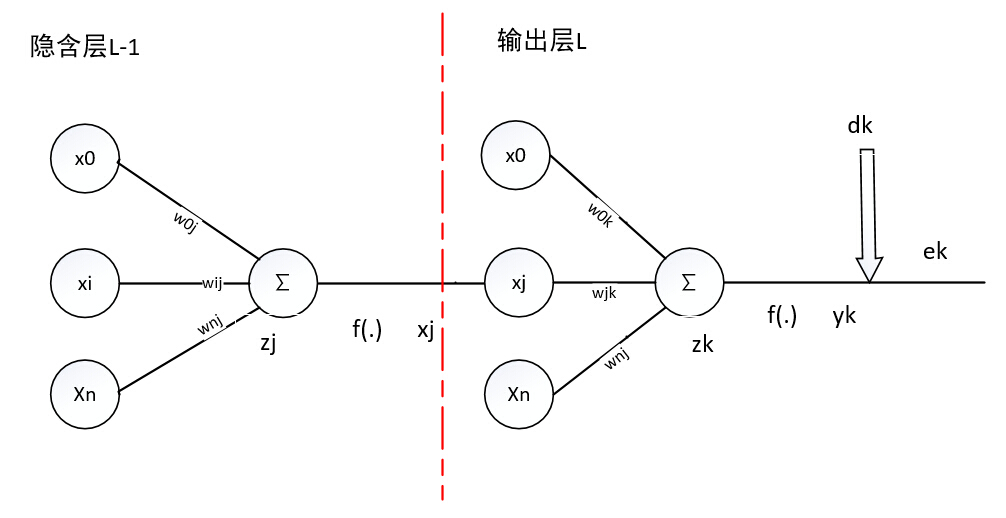
请忽略图中明显的不足、错误之处
各参数：
第 $L-1$层神经元i到神经元j的权值 $w^{L-1}_{ij}$
第 $L-1$层神经元 $j$的加权和：$z^{(L-1)}_j$
$z^{(L-1)}_j = \sum_{i=0}^{i=S_{L-1}}w^{(L-1)}_{ij}x^{(L-1)}_i$

第$L-1$层神经元$j$的敏感度：$\delta^{(L-1)}_j$
第$L-1$层神经元数：$S_{L-1}$

第$L$层神经元j到神经元k的权值$w^{L}_{jk}$
第$L$层神经元$k$的加权和：$z^{(L)}_k$
$z^{(L)}_k = \sum_{j=0}^{j=S_{L}}w^{(L-1)}_{jk}x^{(L)}_j$
第$L$层神经元$k$的敏感度：$\delta^{(L)}_k$
第$L$层神经元数：$S_{L}$
第$L$层神经元$k$的值：$y_k$，这个值也就是对x的预测值
$y_k=f(z^{(L)}_k)$
第$L$层神经元$k$的预测误差:$e_k = y_k-d_k$

第$L$层神经元的平方误差：

$$E=\frac{1}{2}\sum_{k=0}^{k=S_L}e_k^{2}$$

$E$对$w^{L-1}_{ij}$求偏导：

$$\frac{\partial E}{\partial w^{(L-1)}_{ij}} =\frac{\partial E}{\partial z^{(L-1)}_j}\frac{\partial z^{(L-1)}_j}{\partial w^{(L-1)}_{ij}}=- \delta^{(L-1)}_j\frac{\partial z^{(L-1)}_j}{\partial w^{(L-1)}_{ij}}$$

下面分别对上面的链式法则中的各项进行求解

$\frac{\partial z^{(L-1)}_j}{\partial w^{(L-1)}_{ij}}=x^{(L-1)}_i$

$\delta^{(L-1)}_j$的求解，根据上面简单网络模型和链式法则进行求解
先看下面的图

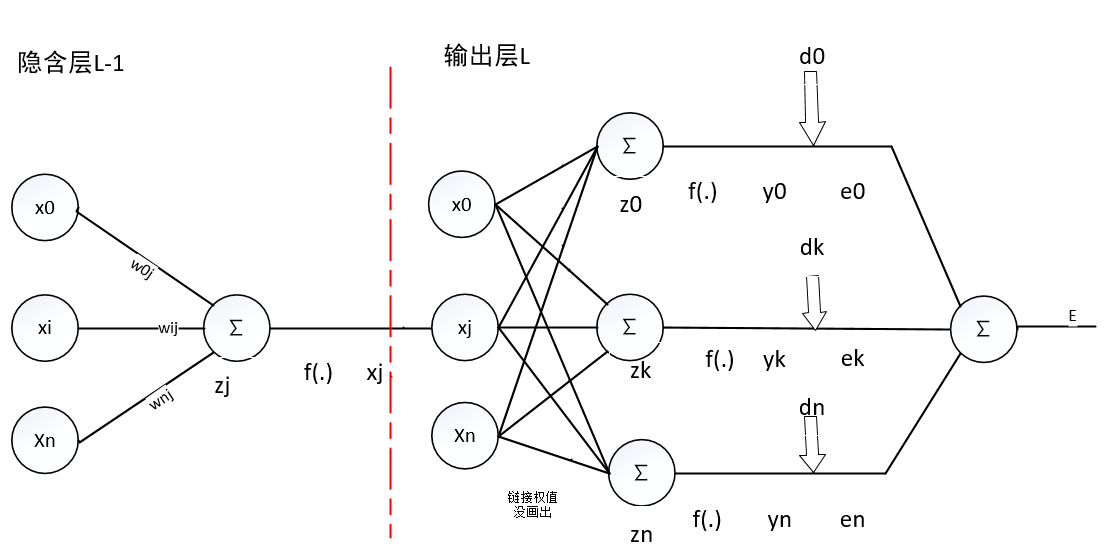
<图中不足之处请见谅>
我们需要求$\delta^{(L-1)}_j \\= - \frac{\partial E}{\partial z^{(L-1)}_j}$
利用链式法则需要对$e_k,y_k,z^{(L)}_k,x^{(L)}_j,z^{(L-1)}_j$求导
我们发现$x^{(L)}_j$对该层的所有加权和都产生了影响，加权和又对$y_k,(k=0,1,S_L)$产生了影响，一直到所有的$e_k,(k=0,1,2,...n)$,最后累加到$E$，所以这个求导要分别对$e_k,(k=0,1,2,3...,S_L)$求导，这里是和的导数，其等于倒数的和。所以：
$\\ \delta^{(L-1)}_j \\= - \frac{\partial E}{\partial z^{(L-1)}_j} \\= -\sum_{k=0}^{k=S_L}\frac{\partial E}{\partial e_k}$
对$e_k$进行链式求导法则
$\delta^{(L-1)}_j \\= - \frac{\partial E}{\partial z^{(L-1)}_j} \\= -\sum_{k=0}^{k=S_L}\frac{\partial E}{\partial e_k}\frac{\partial e_k}{\partial y_k}\frac{\partial y_k}{\partial z^{(L)}_k}\frac{\partial z^{(L)}_k}{\partial x^{(L)}_j}\frac{\partial x^{(L)}_j}{\partial z^{(L-1)}_j}\\=-\sum_{k=0}^{k=S_L}e_k(-1)f^{'}(z_k^{(L)})w^{(L-1)}_{jk}f^{'}(z^{(L-1)}_j)\\=f^{'}(z^{(L-1)}_j)\sum_{k=0}^{k=S_L}e_kf^{'}(z_k^{(L)})w^{(L-1)}_{jk}\\= f^{'}(z^{(L-1)}_j) \sum_{k=0}^{k=S_L}\delta^{(L)}_kw^{(L-1)}_{jk}$

利用梯度下降法更新$w^{(L-1)}_{ij}$

$$w^{(L-1)}_{ij} (n+1)= w^{(L-1)}_{ij}(n) -\eta \Delta w^{(L-1)}_{ij}=w^{(L-1)}_{ij}(n)+\eta \delta^{(L-1)}_j x^{(L-1)}_i$$
或者直接写出：

$$w^{(L-1)}_{ij} (n+1)=w^{(L-1)}_{ij}(n)+\eta \delta^{(L-1)}_j x^{(L-1)}_i$$
其中：
$\eta$是学习率
$\delta^{(L-1)}_j$是第 $L-1$层输出神经元 $j$的敏感度
$x^{(L-1)}_i$表示第 $L-1$层输入神经元 $i$的值
$\delta^{(L-1)}_j=f^{'}(z^{(L-1)}_j) \sum_{k=0}^{k=S_L}\delta^{(L)}_kw^{(L-1)}_{jk}$

根据上面可以得出规律，对于$l$层,隐含层之间利用梯度下降法更新权值系数公式：

$$w^{(l)}_{ij} (n+1)=w^{(l)}_{ij}(n)+\eta \delta^{(l)}_j x^{(l)}_i$$

其中：
$\eta$是学习率
$\delta^{(l)}_j$是第$l$层输出神经元$j$的敏感度
$x^{(l)}_i$表示第$l$层输入神经元$i$的值
$\delta^{(l)}_j=f^{'}(z^{(l)}_j) \sum_{k=0}^{k=S_{l+1}}\delta^{(l+1)}_kw^{(l)}_{jk}$

总结

第$l$层神经元之间的权值系数：

$$w^{(l)}_{ij} (n+1)=w^{(l)}_{ij}(n)+\eta \delta^{(l)}_j x^{(l)}_i$$

当$l==L$也就是隐含层到输出层：

$$\delta^{(l)}_j=e_jf^{'}(z^{l}_j)=(d_j-y_j)f^{'}(z^{l}_j)$$

当$l<=L-1$也就是隐含层之间：

$$\delta^{(l)}_j=f^{'}(z^{(l)}_j) \sum_{k=0}^{k=S_{l+1}}\delta^{(l+1)}_kw^{(l)}_{jk}$$

为了防止出现振荡问题，一种改进的权值修正方法：

$$w^{(l)}_{ij} (n+1)=w^{(l)}_{ij}(n)+\eta \delta^{(l)}_j x^{(l)}_i+\alpha[w^{(l)}_{ij} (n)-w^{(l)}_{ij} (n-1)]$$

其中：
$\alpha$是动量系数，通常取0.2-0.8
对于上面的式子，在一些书中可能形式不一样

BP伪代码：
参数：隐含层数量，隐含层大小，动量系数，学习率
随机初始化各个权值系数
对每个训练样本数据进行训练：
前馈阶段：
利用输入值，权值系数，进行逐步迭代，直到最后输出层
反馈阶段：
利用训练误差，逐步向后更新权值系数
当到达最大迭代次数的时候停止更新

自己整理，符号表示比较复杂，有上标也有下标，还有中标，如有错误请指出