图之Prim算法、kruskal算法和拓扑排序

本文内容部分来源于网易云课堂浙江大学数据结构视频教程，谢谢！！！

1、最小生成树

a、先是一棵树：无回路，v个顶点一定有v-1条边；

b、是生成树：包含全部顶点，v-1条边全在图里；（向生成树中任加一条边都会形成回路）

c、边的权重和最小。

最小生成树一定是连通的，连通图中也一定能找到一棵最小生成树。

贪心算法：贪，每一步都要权重最小。约束条件：1、只能用图里的边，2、只能正好用掉v-1条边，3、不能有回路。

求最小生成树方法一：Prim算法：（让一棵小树长大）

基本思想：

从连通网N={V,E}中的某一顶点U0出发，选择与它关联的具有最小权值的边(U0,v)，将其顶点加入到生成树的顶点集合U中。以后每一步从一个顶点在U中，而另一个顶点不在U中的各条边中选择权值最小的边(u,v),把它的顶点加入到集合U中。如此继续下去，直到网中的所有顶点都加入到生成树顶点集合U中为止。

举例，求下图的最小生成树：

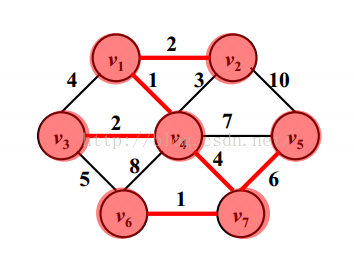
从V1点出发，找到与集合U={v1}相连且权重最小的边(v1,v4)，收录进来U={v1，v4}，之后寻找与 此时的U相连且权重最小的边(v1,v2)（注意，这时候可能有很多权重最小但相等的边，随便选一个即可），此时U={v1,v4,v2}，依此类推。（注意，收录顶点时千万不能形成回路）

求最小生成树方法二：Kruskal算法(将森林合并成树)

算法过程：

1.将图各边按照权值进行排序

2.将图遍历一次，找出权值最小的边，（条件：此次找出的边不能和已加入最小生成树集合的边构成环），若符合条件，则加入最小生成树的集合中。不符合条件则继续遍历图，寻找下一个最小权值的边。

3.递归重复步骤1，直到找出n-1条边为止（设图有n个结点，则最小生成树的边数应为n-1条），算法结束。得到的就是此图的最小生成树。

Kruskal算法因为只与边相关，则适合求稀疏图的最小生成树。而prime算法因为只与顶点有关，所以适合求稠密图的最小生成树。

举例：（还是上面那个图）

发现边(v1,v2)和边(v6,v7)权重都为1，把这两条边收录进来，之后把权重为2的边(v1,v2)和边(v3,v4)加入，依此收入，但注意，收录边时千万不能形成回路

注意：连通图的最小生成树是不唯一的

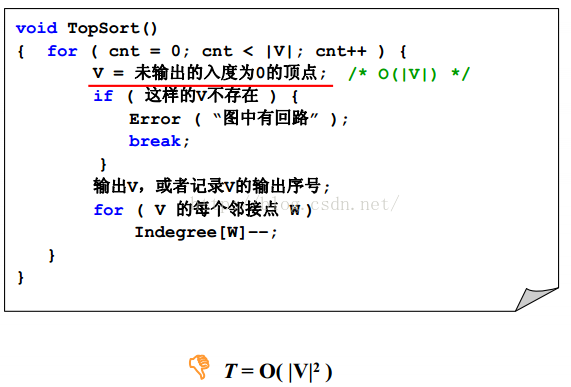
2、拓扑排序

拓扑序：如果图中从V到W有一条有向路径，则V一定排在W之前。满足此条件的顶点序列称为一个拓扑序。

获得一个拓扑序的过程就是拓扑排序。

网络中如果有合理的拓扑序，则必定是 有向无环图。

基本思想：在图中，每次输出没有前驱的顶点。

 

拓扑排序举例：

如下网络：

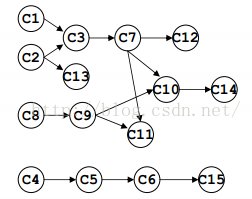
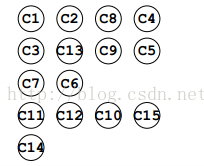
每次都找入度为0的顶点，先排序C1,C2,C8,C4，在排序C3,C13,C9,C5，依次类推，排序结果如下：

拓扑结构的应用：关键路径问题

AOE网络：一般用于安排活动工序，如下图：

 

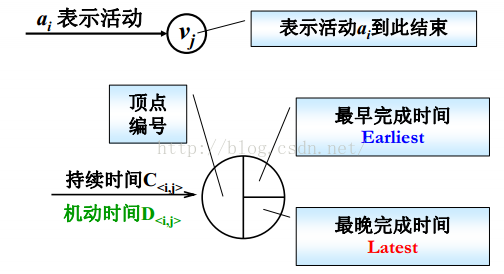
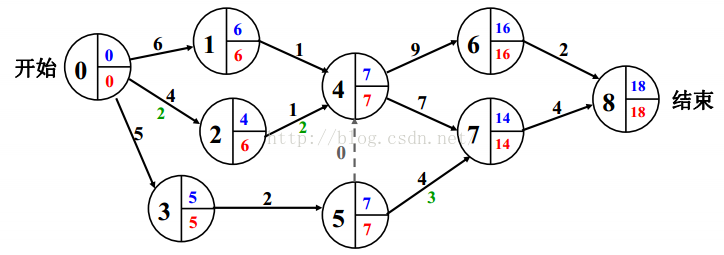
最早完成时间：Earliest[0]=0;Earliest[j]=max{Earliest[i]+C<i,j>;}

机动时间：哪几个组一天都不停，哪几个组有空闲机动时间？如上图例子，在保证18天完工的情况下，看看哪个组可以再干点别的。

机动时间D<i,j>=Latest[j]-Earliest[i]-C<i,j>

最晚完成时间：从结束点往回推，Latest[8]=18;Latest[i]=min{Latest[j]-C<i,j>;}

关键路径：由绝对不能延误的活动组成的路径（没有机动时间的路径）。

关键路径上的活动如果能加快的话，整个项目就能提前完工。