1> pin-hole model:
The functions in this section use a so-called pinhole camera model. In this model, a scene view is formed by projecting 3D points into the image planeusing a perspective transformation.
or
where:
are the coordinates of a 3D point in the world coordinate space
are the coordinates of the projection point in pixels
is a camera matrix, or a matrix of intrinsic parameters
is a principal point that is usually at the image center
are the focal lengths expressed in pixel units.
Thus, if an image from the camera isscaled by a factor, all of these parameters shouldbe scaled (multiplied/divided, respectively) by the same factor. Thematrix of intrinsic parameters does not depend on the scene viewed. So,once estimated, it can be re-used as long as the focal length is fixed (incase of zoom lens). The joint rotation-translation matrix
is called a matrix of extrinsic parameters. It is used to describe thecamera motion around a static scene, or vice versa, rigid motion of anobject in front of a still camera. That is,
translatescoordinates of a point
to a coordinate system,fixed with respect to the camera. The transformation above is equivalentto the following (when
):
Real lenses usually have some distortion, mostlyradial distortion and slight tangential distortion. So, the above modelis extended as:
,
,
,
,
, and
are radial distortion coefficients.
and
are tangential distortion coefficients.Higher-order coefficients are not considered in OpenCV. In the functions below the coefficients are passed or returned as
vector. That is, if the vector contains four elements, it means that
.The distortion coefficients do not depend on the scene viewed. Thus, they also belong to the intrinsic camera parameters. And they remain the same regardless of the captured image resolution.If, for example, a camera has been calibrated on images of320x240 resolution, absolutely the same distortion coefficients canbe used for640x480 images from the same camera while
,
,
, and
need to be scaled appropriately.
The functions below use the above model to do the following:
- Project 3D points to the image plane given intrinsic and extrinsic parameters.
- Compute extrinsic parameters given intrinsic parameters, a few 3D points, and their projections.
- Estimate intrinsic and extrinsic camera parameters from several views of a known calibration pattern (every view is described by several 3D-2D point correspondences).
- Estimate the relative position and orientation of the stereo camera “heads” and compute therectification transformation that makes the camera optical axes parallel.
2> fisheye model:
Definitions:Let P be a point in 3D of coordinates X in the world reference frame (stored in the matrix X)The coordinate vector of P in the camera reference frame is:
class center
where R is the rotation matrix corresponding to the rotation vector om: R = rodrigues(om);call x, y and z the 3 coordinates of Xc:
class center
The pinehole projection coordinates of P is [a; b] where
class center
Fisheye distortion:
class center
The distorted point coordinates are [x’; y’] where
(此处opencv文档有些不清楚, 本人验证并更正如下,附matlab验证代码)
x' = (theta_d / r)* a y' = (theta_d / r)* bFinally, conversion into pixel coordinates: The final pixel coordinates vector [u; v] where:
class center
u = fx * x' + Cx;
v = fy * y' + Cy;
3> other materail
http://wenku.baidu.com/link?url=waSqjF9HJ4BGMGoeL4bLIntrZ24B48jXczOoYz7PBYkoqn8jxZ8HGL8STzvFVdnl8WWEgOg8tcVFoZ4jO_Izo907_DbvLktrpbyd4SQmBMO
http://wenku.baidu.com/view/580fa337ee06eff9aef807cc.html
opencv 鱼眼模型验证:
clear close all R = [0.8988261790903926, 0.4188302467301371, 0.129200325873188; -0.4187798435070649, 0.9076282961426588, -0.02888457570005586; -0.1293636056005076, -0.02814427943910706, 0.9911977386379015]; t = [-0.402431, 0.0388337, 0.671309]'; A = [594.1656343384788, 0, 643.4646451030211; 0, 593.6065468136707, 371.2638324096167; 0, 0, 1]; K = [-0.04192856403922697; -0.002158383400516276; 0.001463386066034605; -0.005204957317263106]; img_data = [ 327.005707, 401.706879, 382.578613, 368.528595, 447.612915, 331.631134, 521.767090, 291.437500, ... 603.254089, 249.857986, 688.284241, 209.167130, 772.313904, 171.579849, 851.017456, 138.804169, ... 921.380676, 111.622528, 982.589966, 89.692650, 355.885986, 474.680847, 413.861481, 445.651489, ... 481.566345, 412.371521, 558.414246, 374.775757, 642.492310, 334.675598, 729.559509, 293.751709, ... 814.828247, 254.507523, 893.690674, 218.945618, 963.500610, 187.922989, 1023.213501, 161.938385, ... 389.184540, 547.380920, 449.031677, 523.005493, 518.651978, 494.009918, 597.481384, 460.122589, ... 682.705994, 422.229462, 770.243408, 381.848572, 855.282410, 341.607635, 933.055847, 303.314911, ... 1001.264832, 268.784271, 1059.156372, 238.558731, 424.892181, 617.114441, 486.681976, 597.320923, ... 557.592102, 572.413391, 636.631287, 542.460144, 721.497192, 507.358459, 807.830017, 468.430420, ... 891.032349, 427.681854, 966.609009, 387.922577, 1032.822144, 350.344391, 1088.560547, 316.416199 ]; obj_data = [ 0.000000, 0.000000,0.100000, 0.000000,0.200000, 0.000000,0.300000, 0.000000, ... 0.400000, 0.000000,0.500000, 0.000000,0.600000, 0.000000,0.700000, 0.000000, ... 0.800000, 0.000000,0.900000, 0.000000,0.000000, 0.100000,0.100000, 0.100000, ... 0.200000, 0.100000,0.300000, 0.100000,0.400000, 0.100000,0.500000, 0.100000, ... 0.600000, 0.100000,0.700000, 0.100000,0.800000, 0.100000,0.900000, 0.100000, ... 0.000000, 0.200000,0.100000, 0.200000,0.200000, 0.200000,0.300000, 0.200000, ... 0.400000, 0.200000,0.500000, 0.200000,0.600000, 0.200000,0.700000, 0.200000, ... 0.800000, 0.200000,0.900000, 0.200000,0.000000, 0.300000,0.100000, 0.300000, ... 0.200000, 0.300000,0.300000, 0.300000,0.400000, 0.300000,0.500000, 0.300000, ... 0.600000, 0.300000,0.700000, 0.300000,0.800000, 0.300000,0.900000, 0.300000]; %% import data img_point = zeros(2, 40); obj_point = zeros(3, 40); img_pre = zeros(2, 40); obj_pre = zeros(3, 40); for n = 1: 40 img_point(1, n) = img_data(2*n - 1); img_point(2, n) = img_data(2*n); obj_point(1, n) = obj_data(2*n - 1); obj_point(2, n) = obj_data(2*n); obj_point(3, n) = 0.0; end figure(1); hold on; plot3(obj_point(1,:), obj_point(2,:), obj_point(3,:), 'r*'); grid on; figure(2); hold on; plot(img_point(1, :), img_point(2, :), 'r*'); axis equal; for n = 1: 40 obj_point(:, n) = R * obj_point(:, n) + t; end figure(1); hold on; plot3(obj_point(1, :), obj_point(2, :), obj_point(3, :), 'b*'); axis equal; %% with no distortion temp = A*obj_point; temp(1, :) = temp(1,:)./ temp(3,:); temp(2, :) = temp(2,:)./ temp(3,:); temp(3, :) = temp(3,:)./ temp(3,:); figure(2) hold on; plot(temp(1, :), temp(2, :), 'b*'); axis equal; %% with distortion for n = 1:40 a = obj_point(1, n) /obj_point(3, n); b = obj_point(2, n) /obj_point(3, n); r = sqrt(a^2 + b^2); theta = atan(r); theta_d = theta* (1 + K(1) * theta^2 + K(2) * theta^4 + K(3)*theta^6 + K(4)*theta^8); temp(1,n) = A(1,1)*(theta_d / r) * a + A(1,3); temp(2,n) = A(2,2)*(theta_d / r) * b + A(2,3); end figure(2) hold on; plot(temp(1, :), temp(2, :), 'g*'); axis equal;
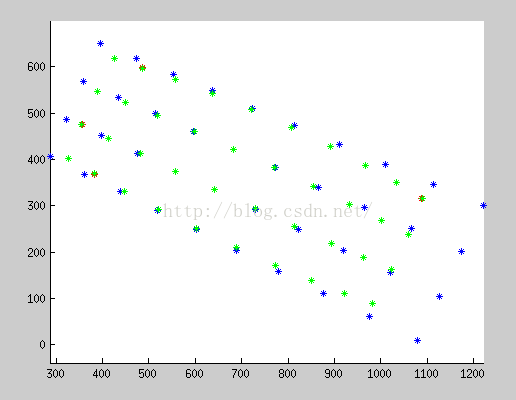
三维点 旋转和平移:
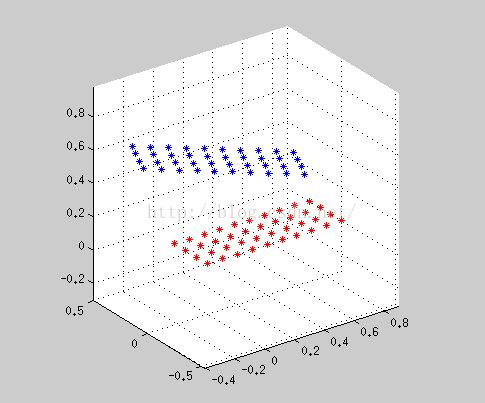
蓝点: 无鱼眼畸变的投影;绿色:有鱼眼畸变的投影; 红色:原图特征点 (红点与绿点重合度越高表明模型越精确)
放大后的误差对比
相机模型(来自opencv documentation)
最新推荐文章于 2023-11-25 23:45:03 发布








![s \; m' = A [R|t] M'](http://docs.opencv.org/2.4/_images/math/363c6d531e851a1eb934e7d6f875d593e2dc6f37.png)
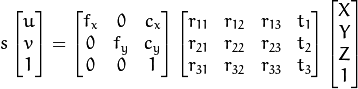
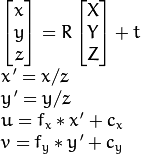
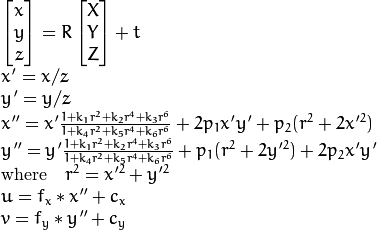
![(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6]])](http://docs.opencv.org/2.4/_images/math/c4c47b9554bab572f9e3ea8d7b0be7eeb8b7c6e5.png)
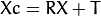
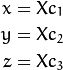
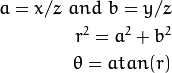
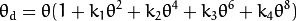














 1048
1048











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








