归并排序与快速排序

分治法

分治法的思想：将原问题分解为几个规模较小但类似原问题的子问题，递归的求解这些子问题，然后合并这些子问题的解来建立原问题的解。及分而治之

分治模式在每层递归时都有三个步骤：
分解原问题为若干子问题，这些子问题是原问题规模较小的实例
解决这些子问题，递归地求解各子问题。然而，若子问题的规模足够小，则直接求解。
合并这些子问题的解成原问题的解。

归并排序

归并排序算法完全遵循分治模式。只管上其操作如下：
分解：分解待排序的$n$个元素的序列成各具有$n/2$个元素的两个子序列。
解决：使用归并排序递归地排序两个子序列
合并：合并两个已经排好序的子序列以产生已排序的答案。

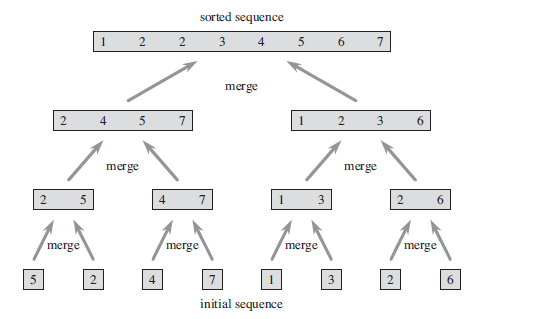
归并排序其排序过程如下图所示：

因此，归并排序算法的核心思想在于合并而不是分解。

归并操作，将两个排好序的数组归并和一个排好序的数组

    /**
     * 将两个排好序的数组arr[p, q-1] 和 arr[q, r]归并成一个排好序的数组arr[p, r]
     * @param arr 数组
     * @param p 左边数组的起始位置
     * @param q 左边数组的结束位置但不包含
     * @param r 右边数组的结束位置
     */
    private static  void merge(Comparable [] arr, int p, int q, int r) {
        int leftN = q - p;  //左边数组元素个个数
        int rightN = r - q + 1;     //右边数组元素的个数

        // 临时开辟两个数组
        Comparable [] left = new Comparable[leftN];
        Comparable [] right = new Comparable[rightN];

        System.arraycopy(arr, p, left, 0, leftN);
        System.arraycopy(arr, q, right, 0, rightN);

        int i = 0, j = 0, k = p;
        while (i < leftN && j < rightN) {
            if (left[i].compareTo(right[j]) < 0)
                arr[k++] = left[i++];
            else
                arr[k++] = right[j++];
        }

        while (i < leftN)
            arr[k++] = left[i++];
        while (j < rightN)
            arr[k++] = right[j++];
    }

因此归并排序算法的递归实现为：

    /**
     *将数组arr[fromIndex, endIndex]进行排序
     * @param arr 要排序的数组
     * @param fromIndex 数组的起始位置
     * @param endIndex  数组的结束位置
     */
    public static void mergeSort(Comparable [] arr, int fromIndex, int endIndex) {
        if (fromIndex < endIndex) {
            int mid = fromIndex + (endIndex - fromIndex) / 2;
            mergeSort(arr, fromIndex, mid);
            mergeSort(arr, mid + 1, endIndex);
            merge(arr, fromIndex, mid+1, endIndex);
        }
    }

对序列{5,2,4,7,1,3,2,6}递归求解过程如下图所示

归并排序还可使用非递归实现，其过程刚好与递归实现相反。对于任意一个序列刚开始时有序序列的长度为1，（及左右排好序的数组的长度为1）。进行归并之后有序学列长度为2，一直讲这个过程重复下去直到有序序列大于等于数组的长度。其源码实现见github。

快速排序算法

快速排序算法也是用分治的思想。但是快速排序与归并排序不一样的是，快速排序可以进行原址排序，不需要额外的申请空间。
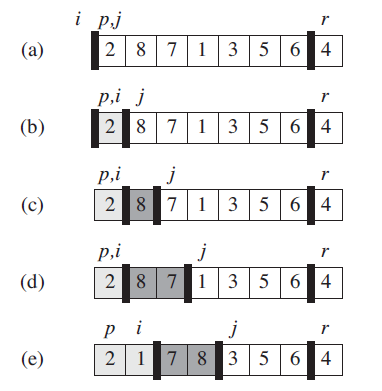
快速排序的思想就是，选定一个主元(pivot element)，将数组中比主元小的元素放在主元的左边，比主元大的元素放在主元的右边。

对于一个典型子数组$A[p ... r]$进行快速排序的散步分治过程：
分解：数组$A[p..r]$被划分为两个(可能为空)子数组$A[p..q-1]$ 和 $A[q+1 .. r]$，使得$A[p..q-1]$中的每一个元素都小于$A[q]$。而数组$A[q+1..r]$中的元素都大于$A[q]$。
解决：通过递归调用快速排序，对子数组子数组$A[p..q-1]$和 $A[q+1 .. r]$
合并：因为子数组都是原址排序的，因此不需要合并操作

Talk is cheap,show me the code!

    /**
     * 使用快速排序算法对数组arr进行排序
     * @param arr 要排序的数组
     * @param fromIndex 要排序的起始位置
     * @param endIndex  要排序的结束位置
     */
    public static void quickSort(Comparable [] arr, int fromIndex, int endIndex) {
        if (endIndex <= fromIndex)
            return;

        //adjustPivot(arr, fromIndex, endIndex);
        int pivot = endIndex; //选择数组中最后一个元素作为主元
        int left = fromIndex-1, right = endIndex+1;
        while (true) {
            // 找到左边比主元大的元素
            while (arr[++left].compareTo(arr[pivot]) < 0) ;
            // 找到右边比主元小的元素
            while (arr[--right].compareTo(arr[pivot]) > 0) ;

            if (left < right)
                swap(arr, left, right); //交换arr[left]与arr[right]的值
            else
                break;
        }
        //将主元放入正确的位置
        swap(arr, left, pivot); 
        //递归排序左右两边子数组
        quickSort(arr, fromIndex, left-1);
        quickSort(arr, left+1, endIndex);
    }

快速排序对于数组集比较大时，其效率是非常高的。但是当数据集比较小时，由于存在递归调用栈的开销其效率并不见得要比shell排序好。因此，可以将快速排序算法进行调整，当元素比较小时使用插入排序，当元素比较多时使用快速排序。
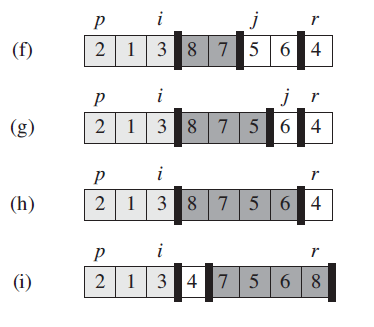
快速排序对主元不同的选择，其效率不一样，一种效率比较高并且常用的主元选择法为选择A[beg] , A[mid], A[end]三个元素的中位数。(mid = (beg+end)/2)

代码为

    public static void sort(Comparable [] arr, int p, int r) {

        if (endIndex - fromIndex >= CUTOFF) { //设置一个门限值
            //调整主元
            adjustPivot(arr, p, r);
            Comparable pivot = arr[r];
            int i = p-1, j = p;
            for (; j <= r-1; ++j) {
                if (arr[j].compareTo(pivot) < 0) {
                    i++;
                    swap(arr, i, j);
                }
            }
            swap(arr, i+1, j);

            sort(arr, p, i);
            sort(arr, i + 2, r);
        } else {
            shellSort(arr, p, r);
        }
    }

上面代码与quicksort代码有点区别但是原理都是一样的。
附上一个主元调整的“栗子”。

附上完整代码：https://github.com/liangpj/AlgorithmsJava.git