【阅读笔记】An overview of gradient descent optimization algorithms

An overview of gradient descent optimization algorithms

原文链接:http://sebastianruder.com/optimizing-gradient-descent/index.html

几种不同的梯度下降法

几种梯度下降法的区别在于我们一次用多少数据来计算目标函数的梯度
我们需要在参数更新的准确性和一次更新花费的时间上权衡利弊，确定一次用多少数据

Batch gradient descent(BGD)

还有个名字叫Vanilla gradient descent
BGD即批量梯度下降，一次会使用全部的数据集来计算参数
θ=θ−η⋅∇θJ(θ)
缺点：很慢、对于那些很大的数据集（内存一次性无法完全装下）毫无办法、不允许在线更新模型（在运行过程中不能增加新的训练样本）
对于凸曲面，BGD可以保证收敛于全局最小值
对于非凸曲面，BGD会收敛于局部的最小值（这不是我们想要的结果）

Stochastic gradient descent（SGD）

SGD即随机梯度下降，对于每一个训练数据（for each training example and label），都会进行参数更新
θ=θ−η⋅∇θJ(θ;x(i);y(i))
BGD用于庞大的数据集的时候，会产生很多的多余计算而不急于去更新参数
SGD则不然，每次都会更新参数，速度更加快，并且可以用于在线学习（运行过程中添加新的训练数据）
缺点：SGD频繁的更新参数，导致目标函数剧烈波动

这样的剧烈波动带来了一些好处，在一个吸引盆（理解为在一个局部最小点，周围很平坦）BGD无法跳出，会收敛于局部这个局部最小值。而SGD（由于其剧烈波动特性）可以跳出这样的陷阱，从而去寻找更有可能成为全局最小值的点
这样的剧烈波动也有一些坏处，当真正达到全局最小值的时候，参数可能会继续波动难以稳定

Mini-batch gradient descent（MBGD）

MBGD即小批量梯度下降法，每一次使用n个样本组成的mini-batch进行训练
也就是说SGD可以看作MBGD的一种特例（n=1）
θ=θ−η⋅∇θJ(θ;x(i:i+n);y(i:i+n))
优点：降低了更新参数的方差，带来更加稳定的收敛；可以利用最新型的深度学习库中高度优化的矩阵运算器，更加高效
Note：一般n的选择在50-256之间，不过应该具体情况具体分析；有时候我们使用小批量梯度下降法的时候，会用SGD（随机梯度下降法）来称呼。比如在Keras中，使用SGD优化器的时候，实际上参数还是基于Mini-batch进行更新的
下文的SGD均指代MBGD

面临的挑战

·合适的学习速率：较小的学习速率会使得收敛缓慢；较大的学习速率会阻碍收敛，使得损失函数在最小值附近波动，甚至发散
·学习速率的自适应：我们可以通过一个预先设定一个方案，或者设定好一个阈值，在训练的过程中调整学习速率（这是非常有用的，因为当我们从一个随机点开始的时候，我们离我们的目标一般很远，一开始需要较大的学习速率，当梯度下降不明显的时候，我们接近目标点，这时需要降低学习速率，使得我们能够准确的收敛于最小值）。我们可以根据预先设定的策略（比如说进行10批次的训练后，降低学习速率，进行50批次的训练后，再次降低），或者当目标函数的变化小于阈值的时候（说明这个时候接近了可能的全局最小值）降低学习速率。但是，这样的方案或者阈值是预先设定的，并不能根据数据集的特性而自适应
·对不同的参数采用不同的学习速率：一般来说我们对于所有的参数，采用相同的学习速率进行更新。但有时候数据比较稀疏（If our data is sparse），不同特征的出现频率也不相同。这时候我们需要对那些出现频率比较小的特征，采用更大的学习速率
·鞍点问题：对于那些非凸误差函数，要避免在那些次优的局部最小值被困住（其实真正的困难会在鞍点出现，在鞍点沿着一个维度斜率上升，沿着另一个维度斜率下降，这些鞍点往往被带有相同误差的点包围，这使得SGD非常难以逃脱，因为在这里沿着任意维度的倒数都接近于0）

梯度下降的优化算法

Momentum

SGD在那些沿着一个方向的陡峭弯曲程度远远大于另一个方向的地方会遇到一些困难，具体表现在其在那些局部极值周围震荡，前进缓慢

Momentum（动量法）增加了一个系数γ，传统方法每一次的更新，只取决于当前的梯度和学习速率，而动量法则加上了一定比例的上一次的更新率。

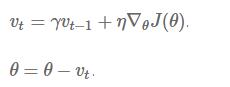
我们可以把它看作一种“惯性”，处于一个“斜坡”这种惯性五行的增大了学习速率，是我们能更快达到最低点（因为我们每一次的更新都增加了一定百分比的上一次更新的量，并且方向相同）；而当我们处在一个“U字型”的局部最小时，当达到局部最小点（或者刚刚过去），传统的算法会使得我们折返，这样就在局部最小值来回波动，最终稳定在这个局部最小值，而无法到达全局最小值，但是如果使用了动量法，我们增加了上一次更新的γ倍的分量，这个分量甚至会大于当前的梯度带来的分量（因为在局部最小值附近的梯度会很小，不足以抵消相反方向的分量）

如下图（图片来源:《1天搞懂深度学习》——李宏毅）

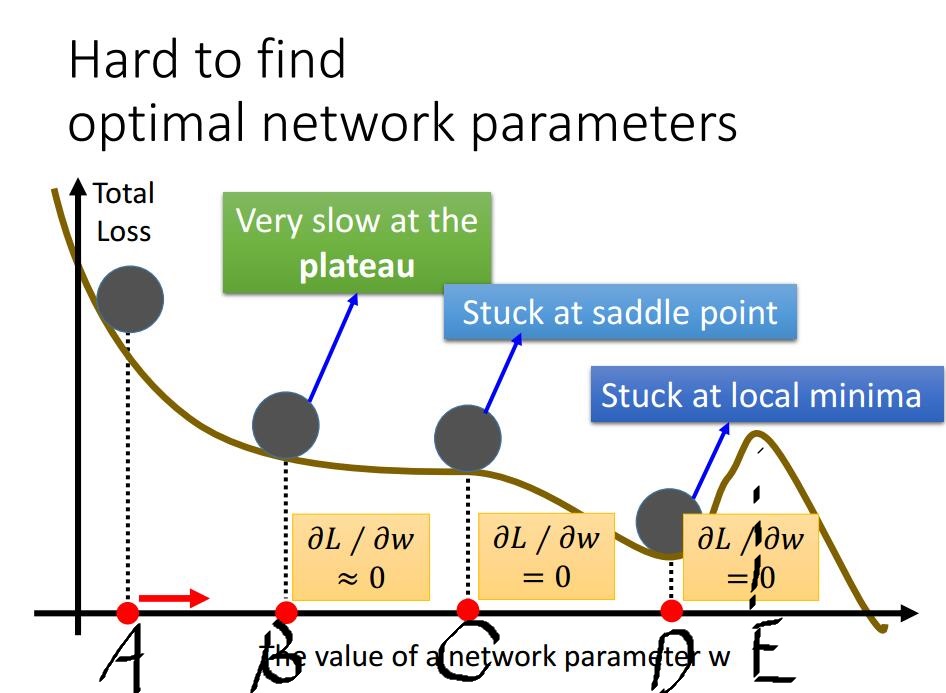
在我们到A-D这一段过程中，由于每一次都加上了一定比例的上一次的参数更新的分量，我们会更快的到达D点；更重要的是，当我们到达D点附近，并不会被卡在D点（在D点，梯度为0，所以移动方向完全取决于上一次更新的方向，会继续向右），这就使得我们可能会冲过E点，继而继续向右，达到更小的点，而不会被D点这个鞍点困住
注意：在一些工具中，公式中的符号（比如γ）可能会不同，这里的γ一般取0.9左右

Nesterov accelerated gradient

在传统的动量法中，如果DE之间的间隔比较短，我们很容易冲过D，达到E的右侧，然后躲开鞍点。但是带来的后果就是，对于这样距离的D和E，我们都会无条件的冲过，比如下图，DE的距离一定的时候，无论这个“小山丘”有多高，我们都会直接越过，而当达到了E右边后，我们自然会继续向右前进。这时候我们相当于增加了一个滤波器，将误差函数中的“横向距离一定的小山丘”全部平滑化（无论有多陡），这相当于无差别的忽略了误差函数中的一些特性，显然是不够好的。

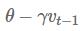
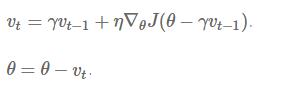
Nesterov accelerated gradient（Nesterov加速梯度法，NAG）改进了这一点，一定系数（γ）的“动量”被保留，但与之相比较的并不是当前的误差函数的梯度，而是根据计算而得到的，“可能的下一时刻所在位置的误差函数的梯度”也就是说当达到D点的时候，我们计算出，传统的动量法可能会到达的点，计算那里的梯度，再和一定比例（γ）的前一次修正的分量进行抵消。

这样的做法带来的大致效果就是，对于途中的实线部分这样的，一边陡峭，一边相对于较为平缓的ravines（小谷…?）我们会冲过，而对于虚线这样的，足够陡峭的误差函数，我们的参数就不会盲目的冲出，并且会很快在D点达到收敛。

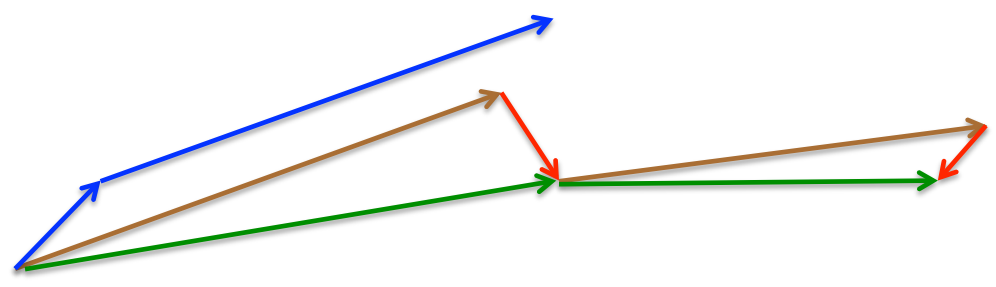
蓝色的就是动量法，第一次移动很短，第二次移动加上了第一次移动的分量，移动了一大步。
而NAG则不同，首先它假设按照Momentum的方案移动（棕色vector），然后计算出这一点的误差函数的梯度，进行修正（红色vector），最后参数真正移动的方向是修正后的方向（绿色vector）。
这种方法避免了过快的（盲目的）前进，提高了算法的响应能力，并且在很多基于RNN的任务上表现出色。
这样我们在斜坡能加速SGD的同时更多的考虑到了误差函数的特性。下边我们希望根据每个参数的重要性来进行不同大小的更新（Adagrad）

Adagrad

Adagrad（Adaptive Gradient，自适应梯度法）是一种基于梯度的优化算法，它会自动调整学习率以适用于不同的参数（对于经常出现的参数采用较小的学习率，而对于很少出现的参数采用较大的学习率），因此更适合处理稀疏数据。
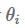
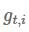
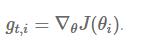
我们另第t次迭代时，对于参数，误差函数的梯度为

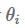
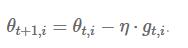
传统的SGD的每一个参数在第t次迭代后的值为

Adagrad修正了学习速率，对于第i个参数的计算：

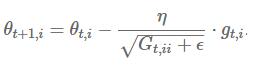
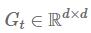
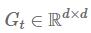
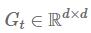
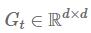
这里的是一个对角矩阵，对角线上的每一个元素，都对应着一个参数，的（i,i）元素，对应第i个参数。而这个值的大小，则是其每次学习的参数的平方和。举个例子，对于第i个参数，对应的（i,i）元素，在第t+1次迭代时，的（i,i）元素的值为θi1^2+θi2^2+…+θit^2。也就是说，参数更新的越频繁，这个分母就会越大，对应的学习速率就会被修正的更小。所以对于经常出现的参数，会逐渐减小其学习速率。拥有一定的自适应能力。
所有的参数一起运算（矩阵运算）：

但是自适应梯度法，也存在着一些问题：
当一次次的迭代过后，对于那些经常被更新的参数，学习率会越来越小，小到最后几乎不会更新。相当于对于每一个参数都有一定的寿命（或者说学习量），迭代到一定程度，就无法继续学习，那么再多的数据也没有用了。
下边的Adadelta算法会解决这个问题

Adadelta

Adadelta是AG（Adagrad）的一个延伸，解决了其不断单调递减的学习速率的问题。Adagrad算法的对角矩阵储存了过去每一次迭代的梯度的平方和，而Adadelta也是储存梯度的平方和，但不会储存过往每一次你迭代的梯度的平方和。
Adadelta算法的梯度平方和的储存矩阵（也是一个对角矩阵）的值仅仅取决于当前这一次迭代的梯度的平方，和上一次迭代的梯度的平方，做一个加权平均，上一次迭代的梯度的平方的权重γ（类似动量法在梯度平方和的一个应用，γ一般也取0.9），而当前这一次迭代的梯度的平方的权重，则为(1-γ)

我们再回顾一遍参数更新的整个过程（用向量的形式）：
传统方法：

Adadelta：

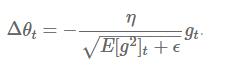
这个表达式分母的形式正是RMS（root mean squared，均方根）的形式，我们可以在公式中将分母简写：
、
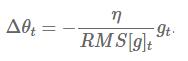
注意：在Adadelta算法更新参数的过程中（SGD,Momentum,Adagrad也是一样），等号的左边和右边的单位并不一致。为了解决这一问题，作者改进了这个算法

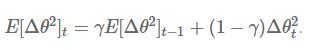
用参数更新值的平方来代替梯度的平方（大概这就是这种方法被叫做Adaptive delta的原因？）
对应的均方根：

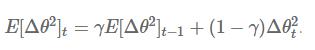
下边对于这个式子

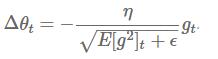
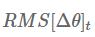
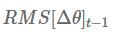
由于是未知的，所以我们用来代替学习速率η。
最终Adadelta算法的更新法则为：

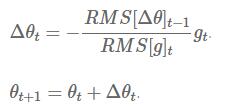
所以在Adadelta算法中，我们甚至不需要去设定一个学习速率η，或者说我们已经将η从更新规则中抹去了

RMSprop

Adam

Visualization of algorithms

Which optimizer to choose?