POJ1159,动态规划经典题目,很适合初学者入门练手。
求:为了使字符串左右对称,应该插入的最小字符数目。
设字符串为S1 S2 S3 … Sn. 这个字符串有n个字符,根据DP的基本思路,减少问题规模。如果S1和Sn匹配,则只关心S2 S3 …Sn-1,就这样问题规模减少了。如果S1和Sn不匹配,那就有两种办法。
方法1:加入S1’,字符串成S1S2 S3 … Sn S1’,则问题转化为S2 S3 … Sn。
方法2:加入Sn’,字符串成Sn’S1S2 S3 … Sn,则问题转化为S1 S3 … Sn-1。
显然,最终结果就是两种方法选最优。
设dp( i, j )表示Si … Sj要变成左右对称的字符串,需要插入的最少字符数目。
状态转换方程:
dp( i, j ) = dp( i+1, j-1 ) if Si == Sj
dp( i, j ) =Min( dp( i+1, j ), dp( i, j-1 ) ) + 1 if Si != Sj
编程实现:采用记忆化递归,比较简单,直接看代码把。
POJ1458,最长公共子序列( LCS ),算法导论上的例子。少说废话,直接看题吧。
设字符串X = X1 X2 X3 … Xn, Y = Y1 Y2 Y3 … Ym.
如果Xn和Ym匹配,那么结果必然是X1 X2 … Xn-1和 Y1 Y2 … Ym-1的LCS + Xn
如果Xn和Ym不匹配,还是有两种选择:
选择1:
LCS的最后一个字符和Xn相同,则问题变成求X1 … Xn和 Y1 … Ym-1的LCS
选择2:
LCS的最后一个字符和Ym相同,则问题变成求X1 … Xn-1和 Y1 … Ym的LCS
设dp( i, j )表示X1 … Xi和 Y1 … Yj的最长公共子序列( LCS )的长度。
状态转换方程:
dp( i, j ) = dp( i+1, j-1 ) +1 if Si == Sj
dp( i, j ) = Max( dp( i+1, j ), dp( i, j-1 ) ) if Si != Sj
呃,是不是感觉和上面的POJ1159有些相似?恩,确实有异曲同工之妙,慢慢体会吧。
编程实现:直接看下文代码。
POJ1141,brackets sequence,括号比配的问题。这题与上面两题有点像,有了上面两题的基础,分析此题也不难。好了,还是看题吧。
求:为了使原来的括号序列匹配,需求加入了最少括号数,而且要知道具体怎么加括号。
因为这题需要打印最终的匹配结果,所以在用DP的时候要多记录一些信息,以方便打印。
设原括号序列为S1 S2 … Sn。
如果S1和 Sn匹配,则相当于求S2 … Sn-1的括号匹配情况。这时最终的匹配结果是:先打印S1,再打印S2 … Sn-1的括号匹配结果,最后打印Sn。
如果S1和 Sn不匹配,怎么办呢?如果把S1 S2 … Sn从中间某个位置(比如Sk)分成两截,问题就变成S1 … Sk和Sk+1 … Sn的情况了。也就是说,把原问题划分成了两个结构相同的子问题。那么,具体从哪划分呢?好像没有什么信息可用,那就从1…n对k进行枚举。因为最终要打印结果,所以还要记录k的值。这时最终的结果是:先打印S1 … Sk的匹配情况,再打印Sk+1 … Sn的匹配情况。
设dp( i, j )表示Si … Sj匹配时,所要加入的最少括号数。
状态转换方程:
dp( i, j ) = dp( i+1, j-1 ) ifS1和 Sn匹配
dp( i, j ) = Min( dp( i, k ) + dp( k+1, j ) ), 其中 i <= k < j ifS1和 Sn不匹配
下图是字符串( [ ( ]的计算过程。
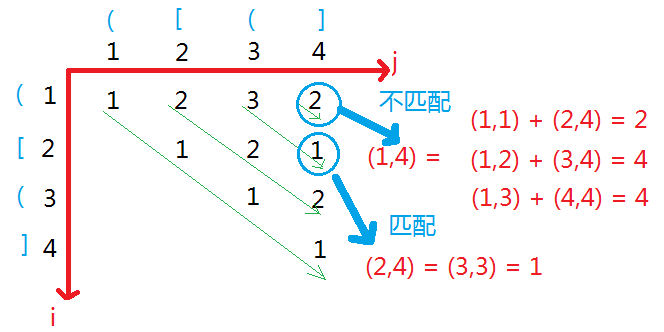
编程实现:算法是有了,不过具体的编程实现还是有点小技巧。嘿嘿,当前主要是针对初学者来说,大牛可完全无视之。
初始条件。当i==j时,dp( i, j ) = ?想想实际情况,只剩下一个括号时,不管它是什么当然不匹配啦。所以必须找到它的另一半才行,故dp( i, i ) = 1
计算顺序。应该沿Z型计算,即i、j之间相差1,i、j之间相差2,…
打印结果。使用递归打印。
POJ1159
#include <iostream>
using namespace std;
//***********************常量定义*****************************
const int MAX = 5000;
//*********************自定义数据结构*************************
//********************题目描述中的变量************************
int size;
char str[MAX];
//**********************算法中的变量**************************
short dp[MAX][MAX];
//***********************算法实现*****************************
//记忆化递归
short Solve( int begin, int end )
{
//如果已经计算过,则直接返回
if( dp[begin][end] >= 0 ) return dp[begin][end];
//如果串的长度为1
if( begin >= end ) return dp[begin][end] = 0;
//如果该串的第一个字符和最后一个字符相同
if( str[begin] == str[end] )
{
return dp[begin+1][end-1] = Solve( begin+1, end-1 );
}
else
{
short x = Solve( begin, end-1 );
short y = Solve( begin+1, end );
return dp[begin][end] = ( x < y ) ? ( x + 1 ) : ( y + 1 );
}
}
//************************main函数****************************
int main()
{
//freopen( "in.txt", "r", stdin );
cin >> size;
for( int i=0; i<size; i++ )
{
cin >> str[i];
}
memset( dp, -1, sizeof(dp) );
cout << Solve( 0, size-1 ) << endl;
return 0;
}
POJ1458
#include <iostream>
#include <string>
using namespace std;
//***********************常量定义*****************************
const int MAX_SIZE = 500;
//*********************自定义数据结构*************************
//********************题目描述中的变量************************
string strX;
string strY;
//**********************算法中的变量**************************
//dp[i][j]表示X0 X1 ... Xi-1和Y0 Y1 ... Yj-1的最大公共子序列的长度
//即dp[i][j]表示X的前i个字符和Y的前j个字符的最大公共子序列的长度
int dp[MAX_SIZE][MAX_SIZE];
//***********************算法实现*****************************
void Solve()
{
int sizeX = (int)strX.size();
int sizeY = (int)strY.size();
//如果有一个串为空,则直接打印结果
if( sizeX == 0 || sizeY == 0 )
{
cout << 0 << endl;
return;
}
//由状态转换方程计算dp[i][j]
for( int i=1; i<=sizeX; i++ )
{
for( int j=1; j<=sizeY; j++ )
{
//计算dp[i][j],要判断Xi-1和Yj-1是否相同
if( strX[i-1] == strY[j-1] )
{
dp[i][j] = dp[i-1][j-1] + 1;
}
else
{
dp[i][j] = ( dp[i-1][j] > dp[i][j-1] ) ? dp[i-1][j] : dp[i][j-1];
}
}
}
cout << dp[sizeX][sizeY] << endl;
}
//************************main函数****************************
int main()
{
//freopen( "in.txt", "r", stdin );
while( cin >> strX >> strY )
{
Solve();
}
return 0;
}
POJ1141
#include <iostream>
#include <string>
using namespace std;
//***********************常量定义*****************************
const int MAX = 105;
const int INF = 999999999;
//*********************自定义数据结构*************************
//********************题目描述中的变量************************
string str;
//**********************算法中的变量**************************
//设str = S0 S1 S2 ... Sn;
//则dp[i][j]表示Si...Sj要构成最短正则括号序列所要增加的括号数目
int dp[MAX][MAX];
//pos[i][j]表示划分str成为两部分的最佳位置
int pos[MAX][MAX];
//***********************算法实现*****************************
void DPSolve()
{
int size = (int)str.size();
//只要一个括号时,必不匹配,要匹配需要另外一个括号
for( int i=0; i<size; i++ )
{
dp[i][i] = 1;
}
//沿之字形填写dp[][]
for( int k=1; k<size; k++ )
{
for( int i=0, j=i+k; i<size && j<size; i++, j++ )
{
//因为要求最小,现将dp[i][j]设置为最大
dp[i][j] = INF;
if( ( str[i] == '(' && str[j] == ')' ) || ( str[i] == '[' && str[j] == ']' ) )
{
dp[i][j] = dp[i+1][j-1];
pos[i][j] = -1;
}
//注意:这里不要用else
//因为要求最小,所以即使比配也要进行下面的处理:例如[][]
//枚举tmp,求划分str的最佳位置
for( int tmp=i; tmp<j; tmp++ )
{
if( dp[i][j] > dp[i][tmp] + dp[tmp+1][j] )
{
dp[i][j] = dp[i][tmp] + dp[tmp+1][j];
pos[i][j] = tmp;
}
}
}
}
}
//根据dp[][],打印结果
void Print( int left, int right )
{
if( left <= right )
{
//当只有一个括号时,直接打印
if( left == right )
{
if( str[left] == '(' || str[left] == ')' ) cout << "()";
if( str[left] == '[' || str[left] == ']' ) cout << "[]";
}
else
{
//如果首尾括号匹配
if( pos[left][right] == -1 )
{
cout << str[left];
Print( left+1, right-1 );
cout << str[right];
}
else
{
Print( left, pos[left][right] );
Print( pos[left][right]+1, right );
}
}
}
}
//************************main函数****************************
int main()
{
//freopen( "in.txt", "r", stdin );
cin >> str;
DPSolve();
Print( 0, str.size()-1 );
cout << endl;
return 0;
}
























 3864
3864

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








