动态规划和贪心算法问题（一）

1.动态规划问题
1.1书面意思
应用于子问题重叠的情况，即不同的子问题具有公共的子子问题。动态规划算法对每个子子问题只求解一次，将其解保存到一个表格中，从而无需每次求解一个子问题时都重新计算，避免了这种不必要的工作。
动态规划方法通常用来求解最优化问题，这类问题可以有很多可行解，每个解都有一个值，我们希望寻找具有最优值的解。设计动态规划算法步骤：
（1） 刻画一个最优解的结构特征
（2） 递归地定义最优解的值
（3） 计算最优解的值，通常采用自底向上的方法
（4） 利用计算出的信息构造一个最优解
1.2 直接上例子
问题1.钢条切割问题：已知长度为i的钢条价格为p[i]，为获取最大收益，对于长度为len的钢条该怎么分割？

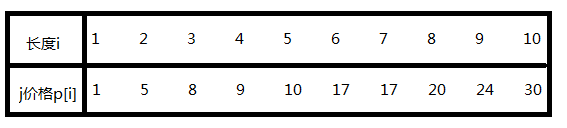
讨论：

 1. len=1，切割方案1=1，收益1；（无切割）
 2. len=2，切割方案2=2，收益5；（无切割）
 3. len=3，切割方案3=3，收益8；（无切割）
 4. len=4，切割方案4=2+2，收益10；
 5. len=5，切割方案5=2+3，收益13；
 6. len=6，切割方案6=6，收益17；（无切割）
 7. len=7，切割方案7=1+6或2+2+3，收益18；
 8. len=8，切割方案8=2+6，收益22；
 9. len=9，切割方案9=3+6，收益25；
10. len=10，切割方案10=10，收益30（无切割） 

注意到：为了求解规模为n的原问题，我们先求解形式完全一样，规模更小的子问题，每次切割，将钢条看成两个独立的钢条切割问题，通过组合两个相关子问题的最优解，并在所有可能的两段切割方案中选取组合收益最大者，构成原问题的解！钢条的切割问题满足最优子结构。
代码实现
（1）自顶向下朴素递归实现

//传入参数是长度为1--10所对应的价格，len表示长度
//len=1对应prices[0];
int cut_rod(int prices[], int len){
    if(len==0)  return  0;      //递归结束的条件
    int sum=INT_MIN;
    for(int i=1;i<=len;i++)
    {
         sum=max(sum,prices[i-1]+cut_rod(prices,len-i));
    }
    return sum;
}
//需要多次递归求解相同的子问题

（2）带备忘录自顶向下-动态规划，付出额外的内存空间来节省时间，每个子问题只求解一次。

//带备忘的自顶向下
memset(memory_p,-1,11*sizeof(int));
emory_p[0]=0;
int cut_rod_memory(int prices[], int len){
    if(len==0)      return 0;
    if(memory_p[len]>=0)    return memory_p[len];//查询是否已经求出对应的部分最优解
    int sum=INT_MIN;
    for(int i=1;i<=len;i++)
    {
            sum=max(sum,prices[i-1]+cut_rod(prices,len-i));
    }
    memory_p[len]=sum;     //保存每一次的结果，大力提升速度（空间换时间）
    return sum;
}

问题2.最长公共子序列 对于给定的两个字符串，计算最长公共子序列（LCS），注意不是子字符串
这是一个最优子问题，前面求出的最长子序列可以供下一次直接使用，判断一下即可

void PrintLCS(char **b,string s,int len1,int len2){
    if(len1==0||len2==0)    return ;
    if(b[len1][len2]=='Y'){
        PrintLCS(b,s,len1-1,len2-1);
        cout<<s[len1-1];
    }else if(b[len1][len2]=='|')
    {
        PrintLCS(b,s,len1-1,len2);
    }else
    {
        PrintLCS(b,s,len1,len2-1);
    }
}
void LCS(string s1,string s2){
    int n1=s1.size();
    int n2=s2.size();
    int **c=new int*[n1+1];//保存LCS长度
    char **p=new char*[n1+1];   //保存路径
    for(int i=0;i<n1+1;i++){
            c[i]=new int[n2+1];
    }
    for(int i=0;i<n1+1;i++){
            p[i]=new char[n2+1];
    }
    memset(&(c[0][0]),0,sizeof(int)*(n1+1)*(n2+1));//清零操作

    for(int i=1;i<n1+1;i++){

        for(int j=1;j<n2+1;j++){
            if(s1[i-1]==s2[j-1]){
                c[i][j]=c[i-1][j-1]+1;
                p[i][j]='Y';
            }
            //此时的LCS即为前期已经确定下来的LCS，比较取得最大的
            else if(c[i-1][j]>=c[i][j-1])
            {
                c[i][j]=c[i-1][j];
                p[i][j]='|';
            }else
            {
                c[i][j]=c[i][j-1];
                p[i][j]='-';
            }
        }
    }
    PrintLCS(p,s1,n1,n2);
}

注意，若是求最长公共子串，代码如下：

int LongestSubstring(string s1,string s2){
    int n1=s1.size();
    int n2=s2.size();
    //c用来保存公共字符串的长度
    int **c=new int*[n1+1];
    for(int i=0;i<n1+1;i++){
        c[i]=new int[n2+1];
    }
    memset(&(c[0][0]),0,sizeof(int)*(n1+1)*(n2+1));

    int maxLen=0;
    int end1=-1;
    int end2=-1;
    for(int i=1;i<n1+1;i++){
        for(int j=1;j<n2+1;j++){
            if(s1[i-1]==s2[j-1]){
                    c[i][j]=c[i-1][j-1]+1;
            }else
            {
                c[i][j]=0;
            }
            if(maxLen<c[i][j]){
                maxLen=c[i][j];
                end1=i;
                end2=j;
            }
        }
    }
    end1--;
    end2--;
    for(;end1>=0&&end2>=0&&s1[end1]==s2[end2];end1--,end2--);

    int start1=end1+1;
    string str=s1.substr(start1,maxLen);
    cout<<str<<endl;

    return maxLen;
}

1.3 数组分割问题的解决（参考）
（1） 将一个无序，元素个数为2n的正整数数组，分割为两部分，使得子数组的和尽可能接近；
分析：怎么确定不同子问题元素个数与数组和的关系？？如果记dp[k]表示取得k个数中数组的和，那么dp[k-1]表示k-1个数的和，我们可以发现k-1个数的最优值和取k个数的最优值之间不存在必然的联系，这样很明显不满足动态规划的最优子问题。也就是说：如果在数组中取k-1个数得到了一个最优值和s1,在数组中取k个数得到了一个最优值s2，s1的组成元素可能就是s2的一部分，也可能不是，没有必然联系。
思路：用dp[k][s]来表示k个元素中和为s的是否存在！！！，存在的都要保存，统一算一遍，看到网上有人贴出这样的计算方式，我也做了一遍，对照结果分析，其实是错误的，具体什么原因自己分析吧！！！

#include<iostream>
#include<string>
#include<algorithm>
#include<numeric>
using namespace std;

#define MAXSUM 10000
#define MAXLEN 100
int main(){
    int A[10]={1,5,7,8,9,6,3,11,20,17};
    bool dp[MAXLEN][MAXSUM];  //k个元素的和为s是否存在？
    memset(&(dp[0][0]),0,sizeof(dp));
    dp[0][0]=true;
    int sum=accumulate(A,A+10,0);
    cout<<sum<<endl;
    for(int k=1;k<=10;k++){
        for(int s=0;s<=sum/2;s++){
            if(s>=A[k-1]){
                dp[k][s]=dp[k-1][s-A[k-1]]||dp[k-1][s];     
            }else
            {
                dp[k][s]=dp[k-1][s];
            }
                cout<<k<<","<<s<<"   "<<dp[k][s]<<endl; 
        }
    }
    int s=sum/2;
    cout<<s<<endl;
    for(;s>=1&&!dp[10][s];s--);
    cout<<s<<endl; 

    system("pause");
    return 0;
}

正确解法：

    //这是很暴力的方式（可以查看迭代结果）
    #include <iostream>  
    #include <algorithm>  
    #include<fstream>
    using namespace std;  

    #define MAXN 101  
    #define MAXSUM 100000  
    int A[MAXN];  
    bool dp[MAXN][MAXSUM];  
    ofstream file("1.txt");
    // dp[k][s]表示从前k个数中去任意个数，且这些数之和为s的取法是否存在  
    int main()  
    {  
        int n, i, k1, k2, s, u;  
        int A[11]={0,1,5,7,8,9,6,3,11,20,17};
        int sum = 0;  
        for (i=1; i<=10; i++)  
            sum += A[i];  
        memset(dp,0,sizeof(dp));  
        dp[0][0]=true;  
        // 外阶段k1表示第k1个数，内阶段k2表示选取数的个数  
        for (k1=1; k1<=10; k1++)            // 外阶段k1  
        {  
            for (k2=k1; k2>=1; k2--)     // 内阶段k2  
                for (s=1; s<=sum/2; s++) // 状态s  
                {  
                    //dp[k1][s] = dp[k1-1][s];  
                    // 有两个决策包含或不包含元素k1  
                    if (s>=A[k1] && dp[k2-1][s-A[k1]])  
                        dp[k2][s] = true; 
                    file<<k2<<","<<s<<"  "<<dp[k2][s]<<endl; //查看迭代结果
                }  
        }  
        // 之前的dp[k][s]表示从前k个数中取任意k个数，经过下面的步骤后  
        // 即表示从前k个数中取任意个数  
        for (k1=1; k1<=10; k1++)  
            for (s=1; s<=sum/2; s++)  
                if (dp[k1-1][s]) dp[k1][s]=true;  
        // 确定最接近的给定值sum/2的和  
        for (s=sum/2; s>=1 && !dp[10][s]; s--);  
        printf("the differece between two sub array is %d\n", sum-2*s);  
        system("pause");
    }  

（2） 将一个无序，元素个数为2n的正整数数组，分割为大小均为n的两部分，使得子数组的和尽可能接近。

    #include <iostream>  
    #include <algorithm>  

    using namespace std;  

    #define MAXN 101  
    #define MAXSUM 100000  
    int A[MAXN];  
    bool dp[MAXN][MAXSUM];  

    // 题目可转换为从2n个数中选出n个数，其和尽量接近于给定值sum/2  
    int main()  
    {  
        int n, i, k1, k2, s, u;  
        n=5;
        int A[11]={0,1,5,7,8,9,6,3,11,20,17};
        int sum = 0;  
        for (i=1; i<=2*n; i++)  
            sum += A[i];           //求出总和
        memset(dp,0,sizeof(dp));  
        dp[0][0]=true;  

        // 对于dp[k][s]要进行u次决策，由于阶段k的选择受到决策的限制，  
        // 这里决策选择不允许重复，但阶段可以重复，比较特别  

        for (k1=1; k1<=2*n; k1++)                // 外阶段k1  
            for (k2=min(k1,n); k2>=1; k2--)      // 内阶段k2  
                for (s=1; s<=sum/2; s++) // 状态s  
                    // 有两个决策包含或不包含元素k1  
                    if (s>=A[k1] && dp[k2-1][s-A[k1]])  
                        dp[k2][s] = true;  
        // 确定最接近的给定值sum/2的和  
        for (s=sum/2; s>=1 && !dp[n][s]; s--);  
        printf("the differece between two sub array is %d\n", sum-2*s);  
        system("pause");
    }