组合数求模总结

本文对C(N,M) mod P介绍三种针对不同数据范围的算法。

例一：FZU2020

数据范围n, m, p (1 <= m <= n <= 10^9, m <= 10^4, m < p < 10^9, p是素数) 

C(N,M)=N*(N-1)*(N-2)*...*(N-M+1)/M!

注意到m非常小，分子分母都有m项于是可以O(m)暴力求出分子分母mod p的值。

又因为m<p且p为质数，所以m！与p互质，于是可以直接求逆元，即(m！)^(p-2)。

时间复杂度O(m+log2p)，空间复杂度O(1)。

code：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <string>
using namespace std;
typedef long long LL;
LL n,k,p,a,b;
int get()
{
    int f=0,v=0;char ch;
    while(!isdigit(ch=getchar()))if(ch=='-')break;
    if(ch=='-')f=1;else v=ch-48;
    while(isdigit(ch=getchar()))v=v*10+ch-48;
    if(f==1)return -v;else return v;
}

LL Pow(LL a,LL b,LL p)
{
    LL res=1;
    for(;b>0;b/=2)
    {
        if(b%2==1)res=res*a%p;
        a=a*a%p;
    }
    return res;
}

int main()
{
    int t=get();
    while(t--)
    {
        n=get(),k=get(),p=get();
        a=1,b=1;
        for(int i=1;i<=k;i++)a=a*(n-i+1)%p,b=b*i%p;
        b=Pow(b,p-2,p);
        printf("%d\n",a*b%p);
    }
    return 0;
}

例二：BZOJ2982

数据范围1<=m<=n<=200000000，p=10007。

本题相比例一m范围增加到2*10^8。而p只有10007，且为质数。

于是可以直接运用lucas定理。

Lucas定理：

where

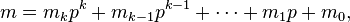
and

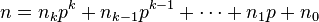
有了这个就可以直接将m,n拆分成p进制。

对于C(Nk,Mk)mod p的求法可以转化为例一在O(P)的时间内求解。

时间复杂度O(p)，空间复杂度O(p)。

code：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <string>
using namespace std;
const int p=10007;
int n,k,inv[p],fac[p],a[10],b[10],len,ans;
int get()
{
    int f=0,v=0;char ch;
    while(!isdigit(ch=getchar()))if(ch=='-')break;
    if(ch=='-')f=1;else v=ch-48;
    while(isdigit(ch=getchar()))v=v*10+ch-48;
    if(f==1)return -v;else return v;
}

int Pow(int a,int b)
{
    int res=1;
    for(;b>0;b/=2)
    {
        if(b%2==1)res=res*a%p;
        a=a*a%p;
    }
    return res;
}

int C(int n,int k)
{
    if(k>n)return 0;
    if(k==0||n==0||n==k)return 1;
    return fac[n]*inv[k]%p*inv[n-k]%p;
}

int main()
{
    int T=1;
    for(int i=1;i<p;i++)T=T*i%p,inv[i]=Pow(T,p-2),fac[i]=T;
    T=get();
    while(T--)
    {
        n=get(),k=get(); ans=1;
        memset(a,0,sizeof(a));
        memset(b,0,sizeof(b));
        for(len=0;k>0;k/=p)a[++len]=k%p;
        for(len=0;n>0;n/=p)b[++len]=n%p;
        for(int i=1;i<=len;i++)ans=ans*C(b[i],a[i])%p;
        printf("%d\n",ans);
    }
    return 0;
}

例三：HDU3439

题目大意：求n的全排列中有且仅有n-k位错排的方案数mod p。

数据范围(0 <= k<= n <=10^9, 1 <= p <= 10^5, n != 0) 

目标答案即为C(n,k)*f(n-k) mod p，其中f(i)为i！全排列错排方案数。

f(n-k)mod p可以直接找循环节，循环节长度为m*2。

接着要求C(n,k) mod p。本题中p仍很小，但是p不保证为质数，因此不能使用例二的方法。

怎么办呢，先将p分解质因数p=p1^k1*p2^k2.*..*pt^kt。然后想办法分别求出c(n,k)mod pi^ki的值，再用中国剩余定理合并同于方程组即可。

关键就在求出c(n,k)mod pi^ki。

c(n,k)=n!/(k!(n-k)!)。若是我们踢出分子分母中所有质因数pi，那么分母将和pi^ki互质，用扩展欧几里得求其mod pi^ki的逆元即可。

我们可以在O(logPi)的时间内求出分子分母中所含质因数pi的个数，设他们的差为T。

接着所有的问题就转化为求n！踢出质因数p后mod p^c的值，再乘上pi^T。

做法是：预处理F[i]表示从1到i中不能被p整除的数之积。设P=p^c。求1到n按每P个分节。每组的前p-1个数mod P同余,于是不含质因数p的积就是F[n%P]*F[P-1]^(n/P)，对于剩下含因数p的数去除p之后乘积就转化为(n/p)!。就这样转化为相同的子问题！

用一个实例来模拟：20！Mod 9.

20!=(1*2*4*5*7*8*…*16*17*19)*(3*6*9*12*15*18)=(1*2*4*5*7*8)^2*(19*20)*3^6(1*2*3*4*5*6)=F[9-1]^(20/9)*F[20%9]*((20/3)! Mod 9).

其中F[0]到F[9-1]的值为1,1,2,2,8,4,4,1,8。

就这样问题得到完美解决。

时间复杂度为O(Σpi^ki)。空间复杂度O(m)。

code：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <string>
using namespace std;
typedef long long LL;
const int maxn=200003;
int ans,n,k,p,T,F[maxn],c[maxn],a[maxn],t[maxn],tot;
int get()
{
    int f=0,v=0;char ch;
    while(!isdigit(ch=getchar()))if(ch=='-')break;
    if(ch=='-')f=1;else v=ch-48;
    while(isdigit(ch=getchar()))v=v*10+ch-48;
    if(f==1)return -v;else return v;
}

int calc()
{
    F[0]=1,F[1]=0;
    for(int i=2;i<2*p;i++)F[i]=LL(i-1)*(F[i-1]+F[i-2])%p;
    return F[(n-k)%(2*p)];
}

void init(int p)
{
    tot=0;
    int pp=p;
    for(int i=2;i*i<=pp;i++)
    {
        if(p%i!=0)continue;
        a[++tot]=i,c[tot]=1,t[tot]=0;
        while(p%i==0)c[tot]*=i,p/=i,t[tot]++;
    }
    if(p!=1)a[++tot]=p,c[tot]=p,t[tot]=1;
}

void ext_gcd(LL a,LL b,LL &x,LL &y)
{
    if(b==0)
    {
        x=1,y=0;
        return;
    }
    ext_gcd(b,a%b,x,y);
    LL tp=x;
    x=y;
    y=tp-a/b*y;
}

LL Pow(LL a,LL b,int P)
{
    LL res=1;
    for(;b>0;b/=2)
    {
        if(b%2==1)res=res*a%p;
        a=a*a%p;
    }
    return res;
}

LL calc(int n,int p,int _p)
{
    if(n<_p)return F[n];
    return (LL(F[n%p])*calc(n/_p,p,_p)%p*Pow(F[p-1],n/p,p)%p+p)%p;
}

int count(int n,int p)
{
    if(n<p)return 0;
    return n/p+count(n/p,p);
}

int C(int n,int k,int p,int _p,int t)
{
    F[0]=1;
    for(int i=1;i<=p;i++)
        if(i%_p!=0)F[i]=LL(F[i-1])*i%p;else F[i]=F[i-1];
    int t3=count(n,_p)-count(k,_p)-count(n-k,_p);
    if(t3>=t)return 0;
    LL t1=calc(n,p,_p),t2=calc(k,p,_p)*calc(n-k,p,_p)%p;
    LL x,y;
    ext_gcd(t2,p,x,y);
    return (t1*x%p*Pow(_p,t3,p)+p)%p;
}

int work()
{
    int res=0,tp,inv;
    LL x,y;
    for(int i=1;i<=tot;i++)
    {
        ext_gcd(p/c[i],c[i],x,y);
        tp=C(n,k,c[i],a[i],t[i]);
        res+=x*tp*(p/c[i])%p,res%=p;
    }
    return (res+p)%p;
}

int main()
{
    T=get();
    for(int i=1;i<=T;i++)
    {
        n=get(),k=get(),p=get();
        ans=calc();
        init(p);
        ans=LL(ans)*work()%p;
        printf("Case %d: %d\n",i,ans);
    }
    return 0;
}