补码另一种理解

一、二进制补码

我们一般来理解补码都是通过原码和反码，实际上我们还可以通过模数的方式来理解补码。

1、例子引入

例如时钟，就是一个很好的例子：

我们想要将时钟的时针从 4 点转到 11  点，有两种办法，一种是顺时针转动 7 小时，另一种是逆时针转 5 个小时，如果我们定义逆时针为负，则这两种办法就是：

转动 7 小时
转动 -5 小时

从这里我们可以发现 -5 对 12 的模刚好等于 7：

a 对 b 取模的计算与取余计算有所不同，虽然算法都是：

• 首先求整数商： c = [a / b] （[ ]为取整）
• 计算模或者余数： r = a - c * b

但是两者的取整策略不同，取余是向0 方向舍入，而取模则是向负无穷方向舍入。

• 过程
• -5 / 12 向负无穷取整得到 -1 
  -5 - (-1) * 12 = 7

下面我们使用特殊的 12 进制来描述更好理解：

符号 1 2 3 4 5 6 7 8 9  A  B  C
代表 1 2 3 4 5 6 7 8 9 10 11 12

大于 12 则进位

这里我们就可以将 7 作为 -5 的补码，可以将 7 代替 -5 进行运算，从这里就可以发现，补码只是使用正数代替负数来运算，但是这里代替负数运算，还需要一个东西，也就是要将最高位进位舍去（高位溢出）。

 

例如，如果时针在 6 点，想要旋转至 1 点，使用逆时针旋转 5 小时的方法，也就是 6 - 5 = 1，换成 6 + (-5) = 1，也就可以使用 -5 的补码来计算。

 

如果不舍去最高位进位：(6)₁₂ + (7)₁₂ = (13)₁₂。

 

如果舍去最高位进位：(6)₁₂ + (7)₁₂ = (1)₁₂。

可以看到第二种得到的才是我们想要的结果，通过补码，我们只用加法就可以实现 6 - 5 = 1 这个减法运算，并且得到了正确的结果。

2、二进制补码理解

二进制补码的原理与上面的例子的原理是类似的，也是使用正数表示负数，然后将最高位进位舍去，为的就是让 CPU 加法单元可以计算减法，也可以说是将减法转换为加法。

我们下面使用 8 位二进制为例子，我们知道对于 Java 中的 byte 类型以及 C 中的 signed char 类型的范围都是 -128 ~ 127，但是为什么呢？

对于 8 位二进制序列，最多表示 0 ~ 255 共计 256 个数字，现在将 256 个数字分为两部分，前半部分 0~127 （128 个数）为正数，正数就是正数，然后后半部分就是 128~255 （128 个数），这些数用来表示负数，用正数表示负数。

那用后半部分这些正数怎么表示负数呢，或者说怎么计算这些正数对应的负数呢，那就需要我们上面提到的模数这个东西了：

对于上面的 1 位十二进制，模数为12，那对于 8 位二进制，模数是 1 0000 0000 =  = 256，也就是说模数的计算方式是（b为进制数，n为位数）：

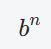
通过 256 这个模数，后半部分的正数 128 ~ 255 减去 256 就可以得到对应表示的负数，例如 128 - 256 = -128，所以 -128 的二进制补码序列就是 128 的二进制序列，也就是 1000 0000，又例如 255 - 256 = -1，所以 -1 的二进制补码序列就是 255 的二进制序列，也就是1111 1111，所以后半部分表示的负数的范围就是-128 ~ -1。

所以计算后半部分的正数的二进制序列所代表的补码对应的负数，就可以使用

正数 - 模数(这里是256)

可以看下标列出的对应关系：

右边二进制序列是谁的补码	二进制序列	左边二进制序列直接转换为十进制
0	0000 0000	0
1	0000 0001	1
2	0000 0010	2
3	0000 0011	3
...	...	...
124	0111 1100	124
125	0111 1101	125
126	0111 1110	126
127	0111 1111	127
-128	1000 0000	128
-127	1000 0001	129
-126	1000 0010	130
-125	1000 0011	131
...	...	…
-3	1111 1101	253
-2	1111 1110	254
-1	1111 1111	255

3、将十进制数转换为二进制补码

1）负数

i.方法一

知道上面的原理， 我们知道范围内的一个负数，如何使用上面的方法计算其补码呢，就可以使用以下方法：

模数 - 负数的绝对值 = 表示对应的负数的正数

然后将这个表示对应负数的正数转换为二进制，就可以得到这个负数的补码

例如 -100 的补码的二进制序列就可以这样求：

256 - |-100| = 156

156 转换为二进制为 1001 1100

所以 1001 1100 就是 -100 的二进制补码序列。

ii.方法二

也可以将模数和要转换的负数的绝对值先转换为二进制，然后进行减法，就可以得到对应负数的二进制补码序列：

(模数)₂ - (负数绝对值)₂ = (负数的补码)₂

例如 -100 的二进制补码序列就可以这样求：

2）正数

当然我们上面说的是负数的补码计算方法，对于正数，其补码就是其原本二进制序列，因为我们上面定义了，在 0 ~ 127 范围内还是正数，正数就是正数，就是自己表示自己，不用进行什么转换。

4、将二进制补码转换为十进制数

1）负数

i.方法一

将二进制补码作为一般二进制序列直接转换为一个十进制正数

这个正数 - 模数 = 补码对应的负数

例如一个二进制补码是 1001 1100，其对应的十进制负数求法为：

将这个二进制序列看做一般二进制序列直接转换为一个十进制正数为 156

156 - 256 = -100

所以这个二进制补码对应的十进制数就是 -100。

ii.方法二

使用模数的二进制减去二进制补码序列就可以得到补码对应的负数的绝对值的二进制。

(模数)₂ - (补码)₂ = (负数的绝对值)₂

最后得到负数的十进制为 -负数的绝对值的十进制

然后将负数的绝对值的二进制转换为十进制，然后加上负号，就可以得到负数的十进制。

例如一个二进制补码是 1001 1100，其对应的十进制负数求法为：

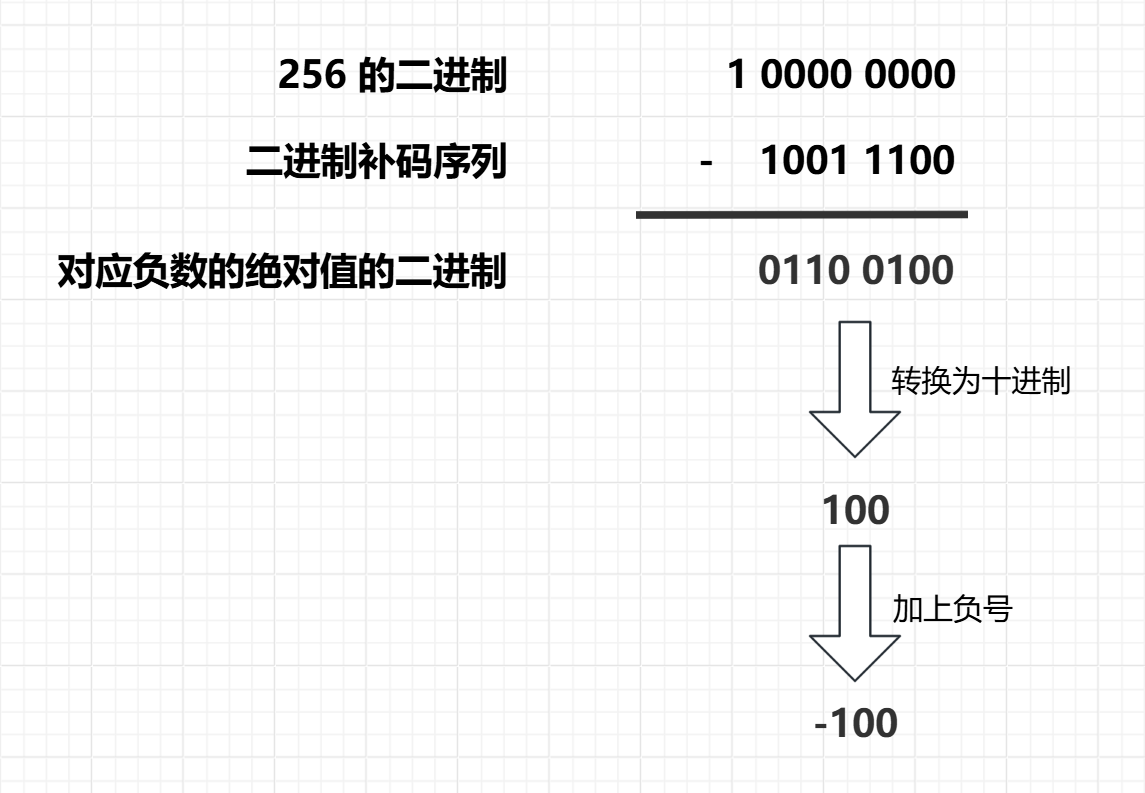
iii.方法三

将补码的二进制序列的最高位的权设为负的，其他位的权还是原先的，

然后按权重计算出十进制数，例如：

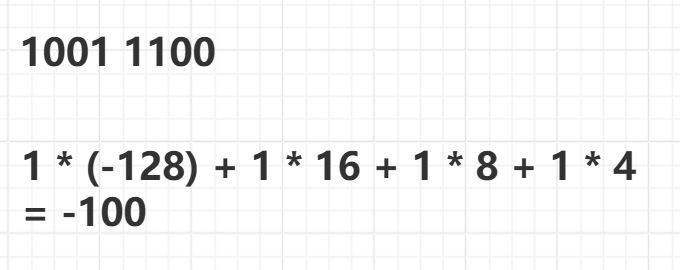
可以得到二进制补码是 1001 1100 对应的负数是 -100。

2）正数

对于正数，将二进制补码转化为十进制数，就是直接将二进制补码序列作为一般二进制序列直接转换为一个十进制正数就可以了，因为正数的补码二进制序列就是这个正数的一般二进制序列。

5、使用二进制补码来代替负数计算

上面的时钟例子中我们给出了使用补码来代替负数进行计算，就可以将减法转化为加法。这里我们同样也举出例子：

例如：

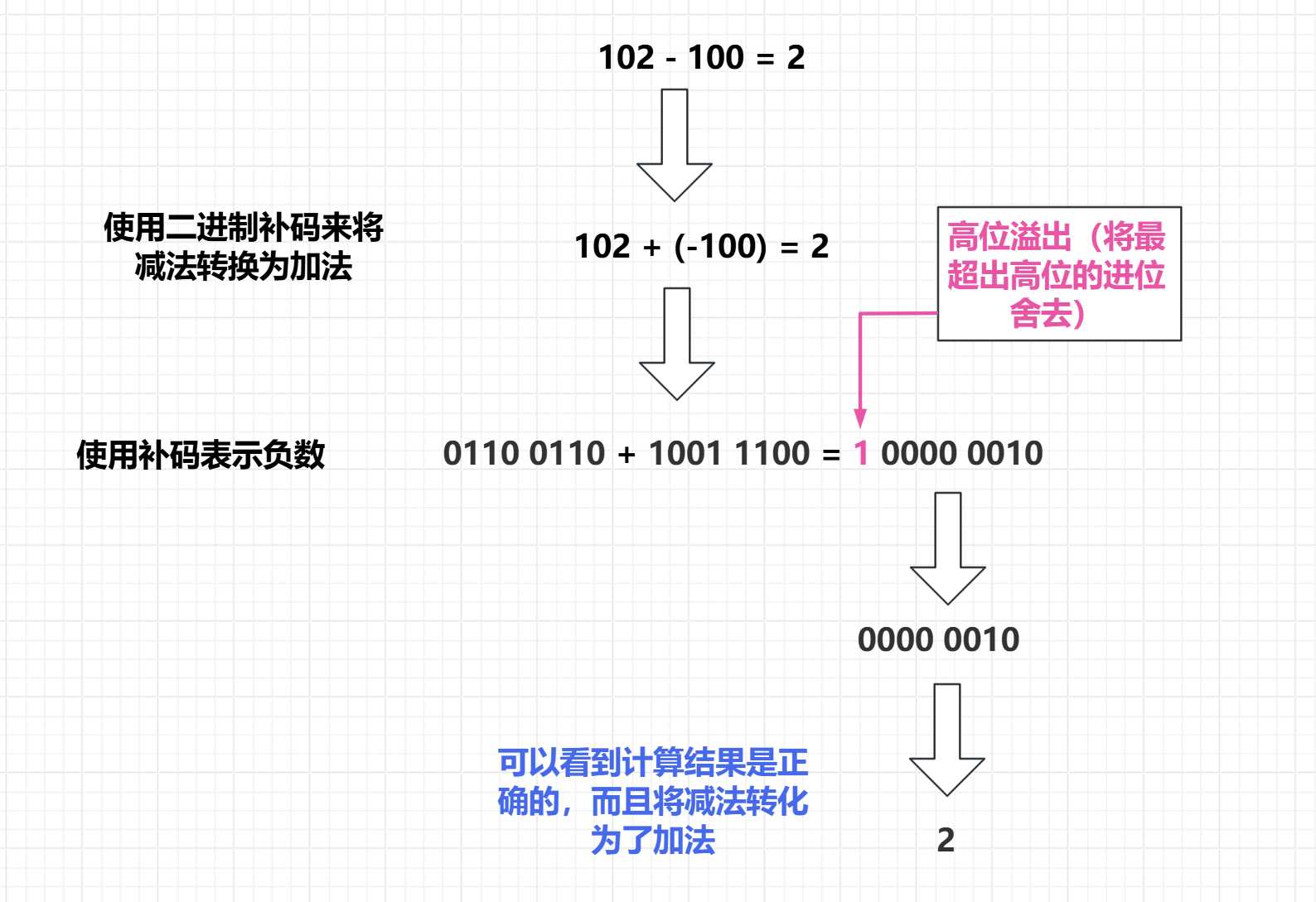
可以发现使用补码，也就是使用一部分正数来代表负数，然后将超出最高位的进位舍去，这种方法可以将减法转换为加法，但是实际上缩减了一个八进制数能表示正数的范围，因为它将一半的正数用来表示负数了。

同时这种使用补码的方法，如果计算数值或者计算结果是超出既定范围的话，结果是难以预测的。

---

本文由大佬@做而论道_CS对我文章Java——二进制原码、反码和补码_原码反码补码-CSDN博客的评论激发而写，同时参考了大佬的文章，感谢大佬的支持。

参考文章：

原码、反码和补码_原码的加法运算进位-CSDN博客