线性保角变换

图像变形之线性保角变换

      线性保角变换（Linear Conformal Transformation）是一种几何形状不变的变换。这种图像变形包括旋转，缩放和平移等。线性保角变换是仿射变换的子集，两者都是常见的空间图像变形。

        下图首先给出了一幅旋转角度为45度，缩放系数为1.5，平移系数为0的线性保角变换的结果：

图1：线性保角变换

        从上图可以看出线性保角变换可以看做是一种带缩放的旋转操作。由于平移（垂直方向，水平方向）只是改变图像的几何位置，这里没有体现出来。在图1中，假设原始图像中某一点的坐标为：（w,z）,线性保角变换后的图像坐标为（x,y），那么有如下的图像变形公式：

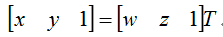                                                                                            （1）

        这里T就是变形矩阵，图1中，线性保角变换的变形矩阵T有如下形式：

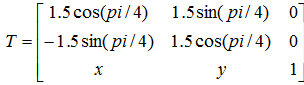，其中x,y是水平平移系数和垂直平移系数。这是线性保角变换的一般格式，角度和缩放倍数可以修改，由于图1中的线性保角变换没有对图像执行平移操作，也就是说x,y的值是0。即变形矩阵为：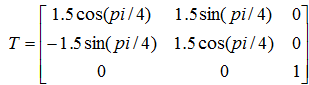

        下面我们可以看看仅有旋转时的效果，如下图所示：

图2：图像旋转

        可以将图像旋转看做是图像线性保角度变换的子集，图2中图像像旋转的变形矩阵为：

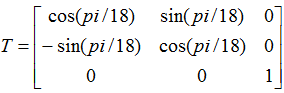，为了理解图像变形的变形矩阵为何是这种方式，我们可以将空域坐标转化到极坐标。如下图所示：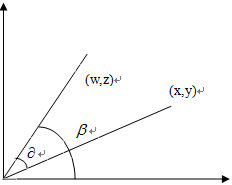

                                                              

                                                                 图3：极坐标系对照图

        在极坐标系中，旋转之前的点（w,z）表示为：