哈夫曼树与哈夫曼编码详解及C++模板实现

　　哈夫曼树又称最优二叉树，是带权路径长度最短的树，可用来构造最优编码，用于信息传输、数据压缩等方面，是一种应用广泛的二叉树。

几个相关的基本概念：

1.路径：从树中一个结点到另一个结点之间的分支序列构成两个节点间的路径
2.路径长度：路径上的分支的条数称为路径长度
3.树的路径长度：从树根到每个结点的路径长度之和称为树的路径长度
4.结点的权：给树中结点赋予一个数值，该数值称为结点的权
5.带权路径长度：结点到树根间的路径长度与结点的权的乘积，称为该结点的带权路径长度
6.树的带权路径长度：树中所有叶子结点的带权路径长度之和，通常记为WPL
7.最优二叉树：在叶子个数n以及各叶子的权值确定的条件下，树的带权路径长度WPL值最下的二叉树称为最优二叉树。

哈夫曼树的建立

由哈夫曼最早给出的建立最优二叉树的带有一般规律的算法，俗称哈夫曼算法。描述如下：
1):初始化：根据给定的n个权值(Ｗ1,Ｗ2,…，Ｗn)，构造n棵二叉树的森林集合F={Ｔ1,Ｔ2,…,Ｔn}，其中每棵二叉树Ｔi只有一个权值为Ｗi的根节点，左右子树均为空。

2):找最小树并构造新树：在森林集合F中选取两棵根的权值最小的树做为左右子树构造一棵新的二叉树，新的二叉树的根结点为新增加的结点，其权值为左右子树的权值之和。

3):删除与插入：在森林集合F中删除已选取的两棵根的权值最小的树，同时将新构造的二叉树加入到森林集合F中。

4):重复2)和3)步骤，直至森林集合F中只含一棵树为止，这颗树便是哈夫曼树，即最优二叉树。由于2)和3)步骤每重复一次，删除掉两棵树，增加一棵树，所以2)和3)步骤重复n-1次即可获得哈夫曼树。

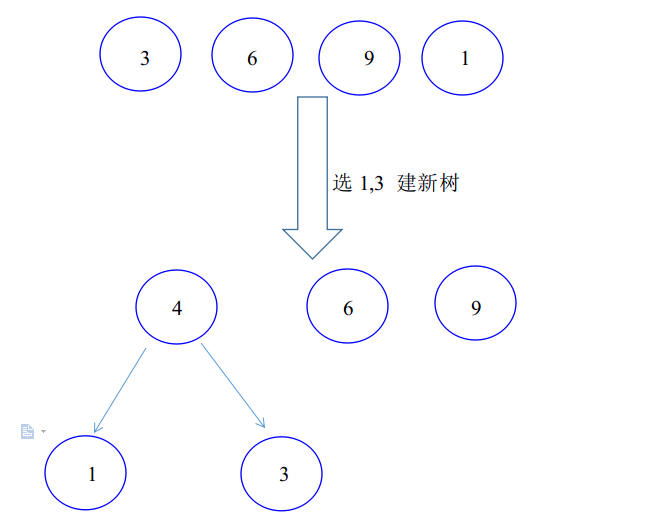
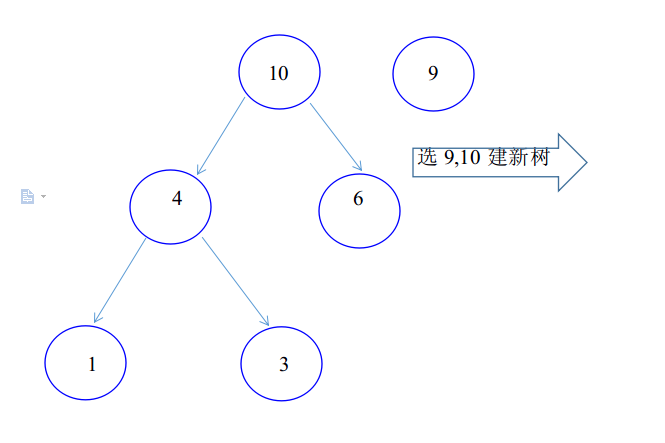
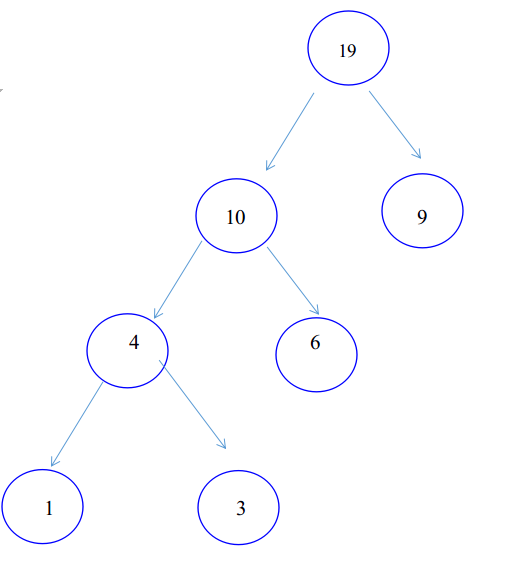
下图展示了有4个叶子且权值分别为{9,6,3,1}的一棵最优二叉树的建立过程。

---

C++类模板构造哈夫曼树

哈夫曼树的节点结构

/*哈夫曼树的节点定义*/
template <typename T>
struct HuffmanNode
{
    //初始化
    HuffmanNode(T k,HuffmanNode<T>* l,HuffmanNode<T>* r):key(k),lchild(l),rchild(r),flag(0) {}

    T key;                  //节点权值
    HuffmanNode<T>* lchild; //节点左孩
    HuffmanNode<T>* rchild; //节点右孩
    int flag;               //标志　判断是否从森林中删除
};

哈夫曼树的抽象数据类型

template <typename T>
class Huffman
{
public:
    void preOrder();        //前序遍历哈夫曼树
    void inOrder();         //中序遍历哈夫曼树
    void postOrder();       //后序遍历哈夫曼树

    void creat(T a[],int size); //创建哈夫曼树
    void destory();             //销毁哈夫曼树
    void print();               //打印哈夫曼树

    void my_sort(int size);
    Huffman():root(NULL) {}
    ~Huffman(){
        destory(root);
    }
private:
    void preOrder(HuffmanNode<T>* pnode);   //前序遍历二叉树
    void inOrder(HuffmanNode<T>* pnode);    //中序遍历二叉树
    void postOrder(HuffmanNode<T>* pnode);  //后序遍历二叉树
    void print(HuffmanNode<T>* pnode);      //打印二叉树
    void destory(HuffmanNode<T>* pnode);    //销毁二叉树

    HuffmanNode<T>* root;           　//哈夫曼树根节点
    HuffmanNode<T>* forest[MAXSIZE];　//用数组来存储森林中树的根节点
};

具体实现

/*自写排序*/
template <typename T>
void Huffman<T>::my_sort(int size)
{
    for(int i=0;i<size-1;i++)
    {
        for(int j=i+1;j<size;j++)
        {
            if(forest[i]->key > forest[j]->key)
            {
                swap(forest[i],forest[j]);
            }
            else
                continue;
        }
    }
};

/*创建哈夫曼树*/
template <typename