数据分享|SAS与eviews用ARIMA模型对我国大豆产量时间序列预测、稳定性、白噪声检验可视化...

原创 于 2023-02-02 16:16:11 发布 · 760 阅读 · 8 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#python #人工智能 #开发语言

文章通过SAS和eviews软件对1957年至2009年的大豆产量历史数据进行时间序列ARIMA模型构建，分析数据的平稳性并建立AR(2)模型。经过白噪声检验，预测未来五年中国大豆产量，提出提高产量的建议，强调预测对于经济决策的重要性。

全文链接：http://tecdat.cn/?p=31480

我国以前一直以来都是世界上大豆生产的第一大国。但由于各国的日益强大，导致我国豆种植面积和产量持续缩减。因此，预测我国的大豆产量对中国未来的经济发展有着极其重要的作用（点击文末“阅读原文”获取完整代码数据）。

我们为一位客户进行了短暂的咨询工作，他正在构建一个主要基于ARIMA的大豆产量预测应用程序，运用SAS与eviews软件对全国1957年到2009年大豆产量的历史数据（查看文末了解数据免费获取方式）建立时间序列ARIMA模型，通过判断其稳定性与是否通过白噪声检验，建立AR（2）模型。最后，因通过残差白噪声检验，对数据进行分析并预测未来五年的我国的大豆产量。

相关视频

一、问题分析

预测未来5年我国的大豆产量及其发展趋势，对国民经济与人民生活都是百利而无一害的。同时，还可以提前让国家了解未来的情况，及时作出应对措施。

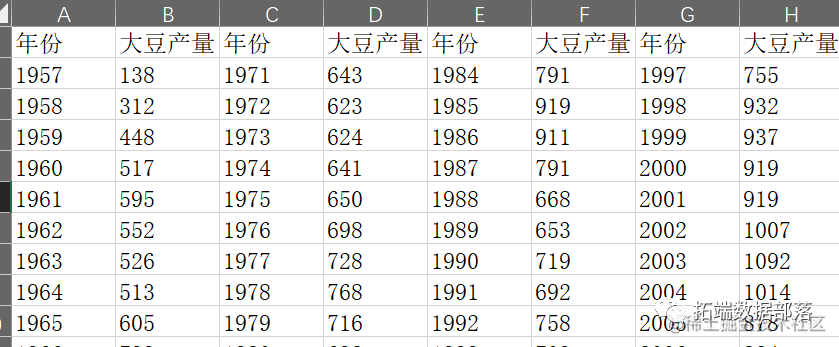
我国的大豆出产量的数据，在此假设所有数据真实可靠（详见下表1），并假设在预测期内不发生任何影响我国的大豆出产量的突发事件。

4b1190056e5eeb6369d7876de52b2fb9.png

difx=dif(x);

year=intnx('year', **'1jan1957'd**,_n_-**1**);

二、模型识别

首先，根据原始数据绘制时间序列图形，观察序列特征。图形如下：

plot x*year difx*year;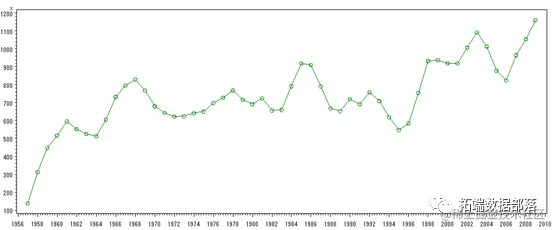

dfa60ff18cf762f9a4d9bd1fc2ab825e.png

图1  我国的大豆产量时序图

点击标题查阅往期内容

ed25a013f4ff89d1ccaf483aaef57396.png

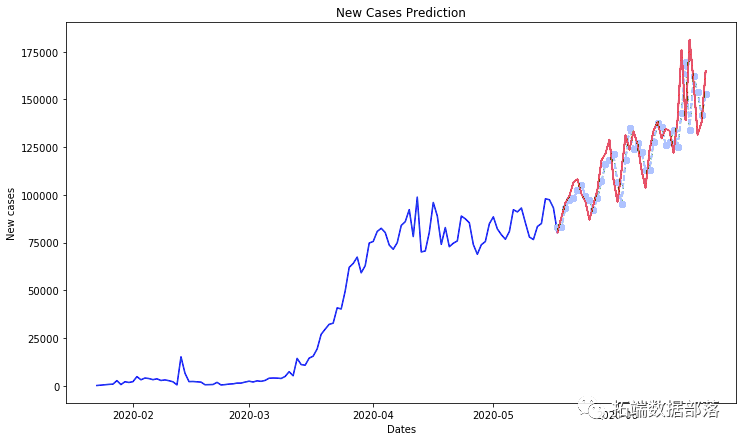
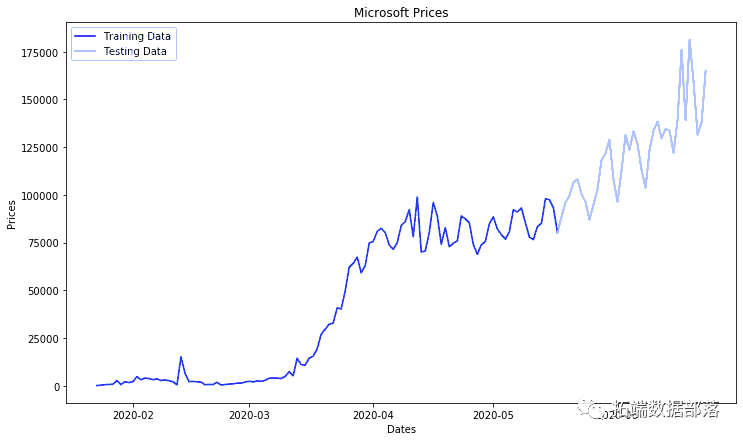
Python用RNN神经网络：LSTM、GRU、回归和ARIMA对COVID19新冠疫情人数时间序列预测

outside_default.png

左右滑动查看更多

outside_default.png

01

3704a27dc7c30a64a5722a6d259837c4.png

02

976c784f08c0d6b7e321ce03ec8839b1.png

03

b6ba32b0a60c0b8614df3c2c7b220681.png

04

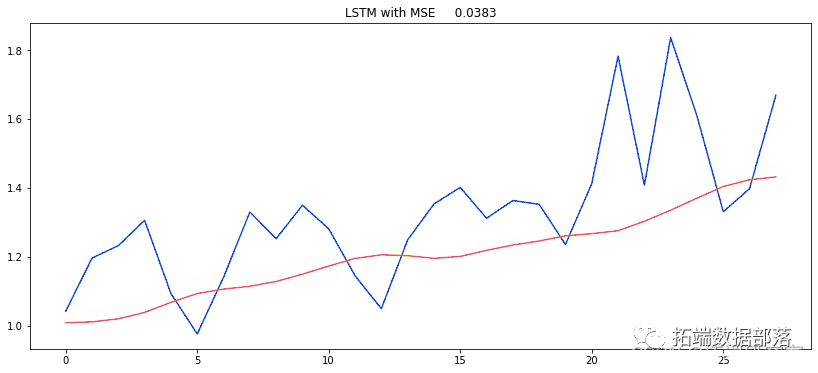
ef9bf60db9cde8a1b8090d2b5da3e4f6.png

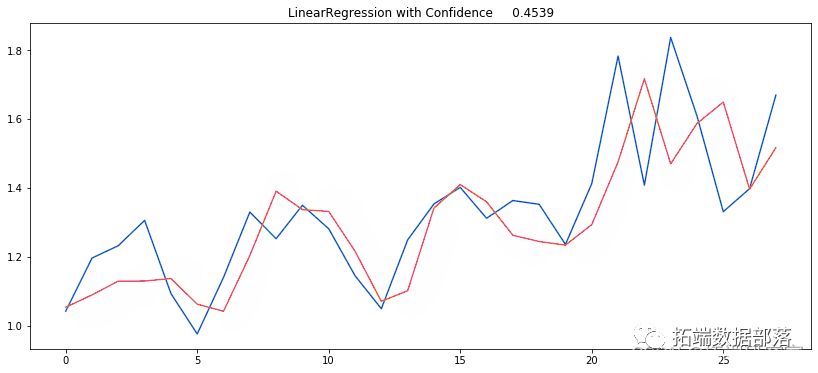
由原始数据的时间序列图可以看出，资料数据呈现明显的上升趋势，其平均数不稳定，是非平稳序列。

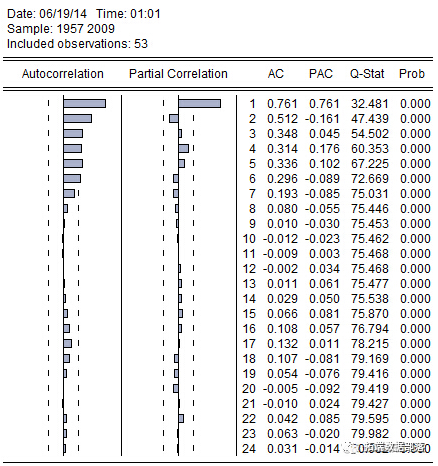
822bd0147854ea06635fa1c341816eee.png

图2 原始序列的自相关图

上图是自相关函数的结果，自相关函数衰减到0的速度缓慢，由此可以再次确定序列是非平稳的。

因为原序列呈现出上升的趋势，故选择1阶差分。1阶差分后的时序图如下所示。

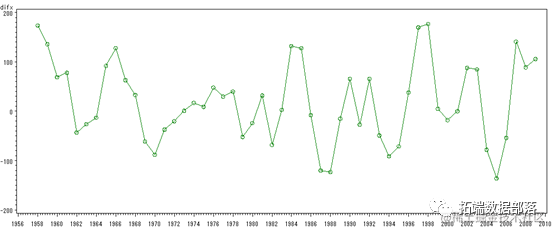
b525bfc93490c8e132b1c6d130583baf.png

图3  1阶差分后的时序图

  由该图可以看出差分后的时间序列在均值附近比较稳定地波动。为了进一步确定平稳性，考察差分后序列的自相关图（如下所示）。

 接下来，我们对差分后的时间序列进行ARMA模型的建立。季节差分后数据的自相关函数如下：

3c0471c469d6075376db36b512633f54.png

图4  1阶差分后的自相关系数图

从上面的分析结果可以看到自相关图显示很强的短期相关性，所以可以初步认为1阶差分后序列平稳。

随后，对1阶差分后序列进行白噪声检验，结果如下图所示。

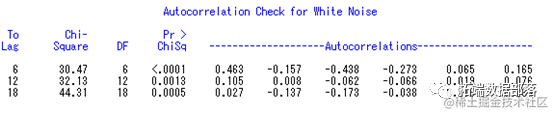
620728a45a37650a44b8aa157acb25ff.png

图5  1阶差分后白噪声检验图

在检验的显著水平取为0.05时，由于上述所有延迟阶数的P值都小于0.05，所以该差分后的序列不能视为白噪声序列，即差分后序列还蕴藏着不容忽视的相关信息可供提取。

1阶差分后序列的自相关图已经显示该序列自相关系数具有拖尾的性质。再考虑其偏自相关系数的性质（见下图）。

1106cc8a1e317a5221d564e662a8363a.png

图6 偏自相关系数图

根据自相关图和偏自相关图的特点，进行模型的定阶。偏自相关图显示，延迟1阶和2阶的偏自相关系数显著大于2倍标准差范围内波动，其他阶数的偏自相关系数都比较小。通过多方面的考虑，最后认为AR（2）模型为最优模型。接着，综合考虑前面的差分运算，实际上是对原序列拟合模型ARIMA(2,1,0)。

三、参数估计

在此，本文采用最小二乘法来估计参数，得到未知参数的估计值为：

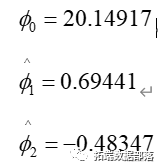
70e641240a997c2fec8d58e831c4cad7.png

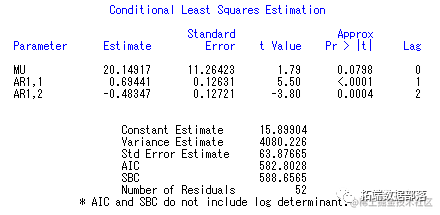
f6a784bf6b457e113aa13574629ba61f.png

图7 参数估计图

四、模型确定

由上面的输出结果可知拟合的方程如下：

0185d025f965081c2358fd6f3206ffe8.png

图8 模型拟合结果图

该输出形式等价于

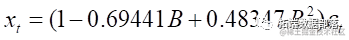
9d43d7fb9a50180d5e01b339c865500a.png

五、模型检验

本文需要检验残差是否有自相关性，由SAS的分析结果得知，不存在自相关性，即残差序列通过白噪声检验。

33ba1fd0fd11b85f1cd5ad245ca30535.png

图9残差白噪声检验

六、模型的预测

本文给出了后面5年的人口自然增长率预测值以及置信区间。

forecast lead=**5** id=year out=out;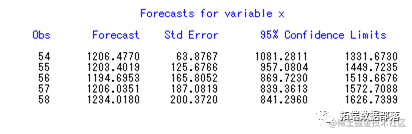

1c0edcf95bca424eb4e531185e53c3ba.png

plot x*year=**1** forecast*year=**2** l95*year=**3** u95*year=**3**/overlay;

图10 预测值以及置信区间

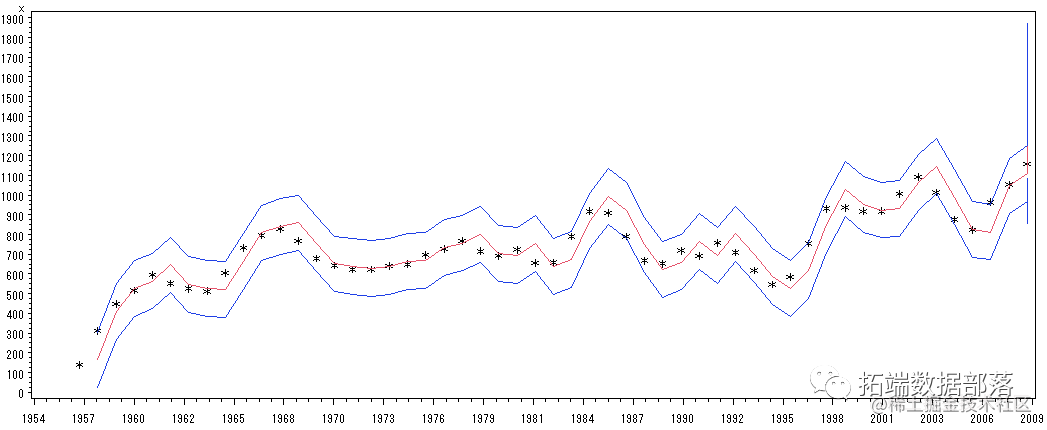
53c3a3c867381eb7a8497c36bab5b8d9.png

通过图示可以直观地看出该模型对序列的拟合效果良好。

七、 总结与建议

从对我国大豆出产量的预测值可以看出，大豆的产量会相对提高，不过提高的速率跟之前的相比也不会相差太大。因此，为了提高我国的大豆产量，我提出了以下几点：

1、为大豆生产提供技术支撑。目前我国水稻、玉米和小麦的单产基本位于国际领先水平，大豆单产却与国际水平有较大差距，这也说明提高我国大豆单产还是很有潜力的。所以，我们应该选育和改良大豆品种，为大豆生产提供优良的种质资源。

2、充分利用我国的自然资源，进一步扩大大豆的种植面积，为扩大我国大豆生产规模和优化区域布局提供保障。

3、提高我国大豆在国际市场的竞争优势，以食品的安全性为主打，向外国销售。

八、 参考文献

[1]应用时间序列分析（第三版），王燕 编著  中国人民大学出版社

数据获取

在公众号后台回复“大豆数据”，可免费获取完整数据。

d91801ecffb48abc3e9abbc0f61723a3.jpeg

本文中分析的数据分享到会员群，扫描下面二维码即可加群！

177fa20e4b8597fc21f0ca9f3afda2f1.png

983e59c571076a7af2908b832887d496.png

点击文末“阅读原文”

获取全文完整代码数据资料。

本文选自《SAS与eviews用ARIMA模型对我国大豆产量时间序列预测、稳定性、白噪声检验可视化》。

点击标题查阅往期内容

R语言使用ARIMAX预测失业率经济时间序列数据

R语言风险价值：ARIMA，GARCH，Delta-normal法滚动估计VaR（Value at Risk）和回测分析股票数据

多元时间序列滚动预测：ARIMA、回归、ARIMAX模型分析

【视频】时间序列分析：ARIMA-ARCH / GARCH模型分析股票价格

时间序列GARCH模型分析股市波动率

PYTHON用GARCH、离散随机波动率模型DSV模拟估计股票收益时间序列与蒙特卡洛可视化

极值理论 EVT、POT超阈值、GARCH 模型分析股票指数VaR、条件CVaR：多元化投资组合预测风险测度分析

Garch波动率预测的区制转移交易策略

金融时间序列模型ARIMA 和GARCH 在股票市场预测应用

时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格

R语言风险价值：ARIMA，GARCH，Delta-normal法滚动估计VaR（Value at Risk）和回测分析股票数据

R语言GARCH建模常用软件包比较、拟合标准普尔SP 500指数波动率时间序列和预测可视化

Python金融时间序列模型ARIMA 和GARCH 在股票市场预测应用

MATLAB用GARCH模型对股票市场收益率时间序列波动的拟合与预测

R语言GARCH-DCC模型和DCC（MVT）建模估计

Python 用ARIMA、GARCH模型预测分析股票市场收益率时间序列

R语言中的时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格

R语言ARIMA-GARCH波动率模型预测股票市场苹果公司日收益率时间序列

Python使用GARCH，EGARCH，GJR-GARCH模型和蒙特卡洛模拟进行股价预测

R语言时间序列GARCH模型分析股市波动率

R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测

matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计

Python使用GARCH，EGARCH，GJR-GARCH模型和蒙特卡洛模拟进行股价预测

使用R语言对S＆P500股票指数进行ARIMA + GARCH交易策略

R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模

R语言股票市场指数：ARMA-GARCH模型和对数收益率数据探索性分析

R语言多元Copula GARCH 模型时间序列预测

R语言使用多元AR-GARCH模型衡量市场风险

R语言中的时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格

R语言用Garch模型和回归模型对股票价格分析

GARCH（1,1），MA以及历史模拟法的VaR比较

matlab估计arma garch 条件均值和方差模型

R语言POT超阈值模型和极值理论EVT分析

656c1f8af10ce7b6088b353261a689a6.png

58e33ed19a33068e133cf4273f4630c0.jpeg

26668ebadefe9ccee2b02cf265065801.png

博客
2025汽车行业洞察报告：智能驾驶、ESG、碳足迹与线控制动|附800+份报告PDF、数据、可视化模板汇总下载
12-19 19
对应人群行动建议：车企可布局可再生能源使用，优化整车能效，加强碳足迹数据核算与披露；智能驾驶正从“技术研发投入”转向“商业价值兑现”，2026年作为L4 RoboX爆发元年，技术成熟度、成本可控性、政策开放性三大要素形成共振，推动行业从B端试点向C端普及跨越，产业链价值重心向算法与运营环节倾斜。2025年，汽车行业正经历“技术重构+商业重塑”的双重变革：智能驾驶从技术验证迈向规模化商用，碳足迹成为产品定价核心锚点，ESG合规重塑供应链合作规则，线控制动技术则在政策松绑与成本优化中实现国产替代突围。
博客
Python用LightGBM、XGBoost、随机森林及Optuna超参数优化的航班票价数据集预测研究
12-19 153
LightGBM的核心目标是最小化正则化目标函数：L(yi,ŷi) + Ω(f)，其中yi为真实票价，ŷi为模型预测票价，L为平均绝对百分比误差（MAPE）损失函数，用于衡量预测值与真实值的相对误差，Ω(f)为正则项（Ω(f)=λT+γ∑j=1Twj²，T为树的叶子节点数，wj为叶子节点权重），用于控制模型复杂度，防止过拟合。注：上述代码补充了数据基本信息探查与相关性分析的核心逻辑，省略了时间特征提取的详细代码，实际项目中需从出发/到达时间中提取小时、星期、月份等特征，增强模型对时间维度规律的捕捉能力。
博客
专题：2025年脑机接口产业蓝皮书：市场规模、专利技术、投融资与临床应用|附40+份报告PDF、数据、可视化模板汇总下载
12-17 14
如今，全球脑机接口企业突破800家，中国企业占比超25%，医疗健康领域应用占比达56%，投融资规模逼近100亿美元，一场关乎“人机协同”的技术革命已进入攻坚突破的关键阶段。中国企业呈现明显的集聚态势，近七成集中在北京、广东、浙江、江苏、上海五地，中小民营企业占比超50%，成为产业创新的主力军。产业上，需完善上下游协同，降低成本、提升普及度。脑机接口产业链呈现“下游主导、中游支撑、上游稀缺”的格局，下游应用企业占比62%，中游制造占30%，上游核心部件仅8%，反映出产业成熟度不足，上游技术亟待突破。
博客
专题：2025医疗行业核心洞察报告：AI医疗、医疗器械、投融资与新药|附380+份报告PDF、数据、可视化模板汇总下载
12-17 38
AI技术显著提升研发效率，将临床试验总体成功率从7.9%提升至17.7%，Phase I到II的成功率从52%提升至80%，这种效率提升吸引资本向AI药物发现技术公司聚集，Tempus AI、XtalPi Technology等企业累计融资均超7亿美元，成为资本追捧的细分龙头。从AI医疗的临床落地信任壁垒，到国产医疗器械的国际化突围，从心血管领域的靶向药技术革新，到基层医疗的效率提升探索，每个细分赛道都在经历技术、政策与市场的多重重塑。公开AI决策的核心依据，加强医患沟通中对AI工具的解释说明；
博客
Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据
12-17 494
我们从商超真实销售数据出发，先通过统计与可视化挖掘品类、单品的销量规律及相关性，再基于历史数据筛选出高潜力单品，最终用深度学习模型实现未来一周销量预测，为补货定价提供可落地的决策依据。长尾单品则可能针对特定消费群体，需求相对小众。而水生根茎类、茄类和食用菌类销量相对较低，且箱线图箱体较窄，说明销量稳定，需求波动小。水生根茎类与花菜类相关系数达0.54，属于强正相关——这意味着当水生根茎类销量上升时，花菜类销量也大概率上升，可能因为两者常搭配烹饪（如清炒时蔬组合），商超可将这两类蔬菜就近陈列，促进连带销售；
博客
专题：2025中国企业跨境出海报告：AI支付、供应链、汽配、黑五|附1000+份报告PDF、数据、可视化模板汇总下载
12-12 93
2025年出海企业海外仓布局中，北美仓占比最高（42%），欧洲仓（31%）、东南亚仓（18%）紧随其后，仓配一体化成为“主流模式”，80%的头部企业选择“国内仓+海外仓”联动布局，实现“时效与成本平衡”。软件出海呈现“技术驱动+本地化运营”双轮驱动趋势，79.8%的出海软件企业采用SaaS订阅模式，52.8%的企业海外收入不足10%，仍处于“探索期”，东南亚、北美是重点市场，AI、营销科技是核心赛道，新加坡、香港成为软件出海的“超级枢纽”。优化移动端购物页面，推出专属折扣券，简化购买流程，提升转化效率。
博客
Python银行客户数据流失预测SMOTE平衡数据实现神经网络、SVM、决策树、随机森林与超参数调优|附代码数据
12-12 800
交叉验证结果与测试集评估一致，随机森林模型的平均准确率最高且分数波动最小（标准差仅0.006），说明其鲁棒性最强，能稳定适配不同批次的客户数据，适合银行实际业务中的批量预测场景。“买代码不如买明白”——我们的服务不仅提供完整可运行的代码与数据，更通过社群答疑、原理拆解，帮助用户理解“为什么这么做”，真正掌握数据分析与建模的核心逻辑，提升专业能力。可与800+行业人士交流成长；核心价值：调优后的模型能多识别1%的潜在流失客户，按银行10万客户规模计算，可帮助银行多挽留1000名客户，直接提升数百万营收。
博客
赢战2025电商新趋势下的增长策略报告：平台格局、跨境趋势、大促消费|附600+份报告PDF、数据、可视化模板汇总下载
12-12 40
原文链接：tecdat.cn/?p=44562原文出处：拓端抖音号@拓端tecdat2025年电商行业正迎来“存量竞争+增量突围”的关键拐点：国内市场从“流量争夺”转向“心智占领”，阿里、抖音等平台形成多元竞合格局；跨境赛道中东南亚、拉美成为新增长引擎，双十一等大促则折射出消费需求向“品质化、细分化”升级（点击文末“阅读原文”获取专题报告合集PDF版本）。数据显示，2025年双十一核心品类销售额突破22亿元，跨境电商GMV同比增速达19.1%，电商榜单对消费决策的渗透率超30%，这些数据共同勾勒出行业变革的
博客
2025机器人行业深度报告：AI驱动、人形化、海外集群|附400+份报告PDF、数据、可视化模板汇总下载
12-09 548
2022-2024年装机量从31台飙到74台，CAGR达55%，2025年上半年又装了40台，天智航市占率30%（方正证券数据），3秒解读：进口品牌不再垄断，国产机在“精度（亚毫米级）+兼容性（适配多品牌假体）”上更懂国内医院；进口品牌为啥不行了？跟本地医保局对接，参考江西（3.38万元/台，医保报92%）、北京（8000元/台，甲类报）的模式，设计“设备租赁+按次收费”方案——比如医院不用买设备，每次手术收5000元服务费，医保报一部分，患者掏一部分，医院没压力，设备商也能持续赚钱。
博客
Matlab、Python用WSO-CNN-GRU、GWO-MLP-RF分析母亲身心健康与婴儿行为数据及SEM、SVM、RF算法
12-09 711
基于此，我们构建了“数据预处理-关联验证-预测建模-聚类评价-策略优化”的全流程分析框架，融合Spearman相关系数、结构方程模型（SEM）、支持向量机（SVM）、随机森林、Kmeans聚类等经典算法，创新引入WSO（白鲨算法）改进的CNN-GRU与GWO（灰狼算法）优化的MLP-RF混合算法，实现了从数据洞察到实际解决方案的闭环。模型拟合结果显示，卡方自由度比1.727（<3）、GFI=0.909（>0.9）、CFI=0.959（>0.9），各项指标均满足拟合标准，模型可靠性良好。
博客
专题：2025年游戏市场洞察报告：市场规模、用户行为、投资趋势|附320+份报告PDF、数据、可视化模板汇总下载
12-09 290
子品类中，回合制RPG增速最猛（138%），核心是《Seven Knights Re:Birth》的爆发——这款“七骑士”IP重制版，上线5个月吸金1.2亿美元，靠的是“经典角色重绘+现代化养成系统”；这提示开发者：在玩法设计中需强化“轻社交”场景，比如加入“亲友组队副本”“社区聊天频道”，避免复杂社交门槛劝退用户。海外厂商不甘示弱，点点互动（77%）、柠檬微趣（101%）靠“本地化运营”突围——比如点点互动《Whiteout Survival》针对韩国玩家调整“雪地场景”美术风格，付费率提升15%。
博客
专题：2026年中国消费零售行业新图景报告：消费者行为、品牌增长与AI应用|附540+份报告PDF、数据、可视化模板汇总下载
12-05 409
对应人群行动建议：品牌方可减少“纯折扣”宣传，转而做“产品实测”“用户故事”等内容（如美妆品牌拍“真实用户30天上脸效果”，服装品牌分享“顾客穿搭场景”）；服装品牌可推出“四季款”（如百搭基础款），减少过季库存压力；：面对46%的营销无感率，下月可测试“产品实测+用户故事”的内容形式——比如服装品牌拍摄“真实用户穿30天的洗涤、版型变化”短视频，食品品牌收集“用户家庭用餐场景”故事（如“妈妈用XX产品给孩子做早餐”），在微信视频号、抖音投放后，监测点击率、互动率，对比传统折扣广告的效果，筛选最优内容方向。
博客
专题：2025半导体行业核心趋势与市场动态报告：AI驱动、先进封装|附130+份报告PDF、数据、可视化模板汇总下载
12-05 754
从材料器件的国产替代攻坚，到资本支出的全球分化，从企业盈利的结构性增长，到产业链环节的协同爆发，每个维度都暗藏“增长机遇与突围挑战”的双重逻辑。AI芯片需求重构全球先进封装市场，呈现“持续高增长”态势：2023年市场规模378亿美元（2.5D/3D封装145亿美元，其他先进封装233亿美元），2025年预计476亿美元（2.5D/3D封装185亿美元，其他291亿美元），2029年将达695亿美元（2.5D/3D封装345亿美元，其他350亿美元），2023-2029年复合年增长率约11%。
博客
专题：2025AI产业应用与投资趋势报告：技术选型、行业落地与效益洞察|附900+份报告PDF、数据、可视化模板汇总下载
12-05 568
显示，开发者评估全托管AI服务时，“输出质量”（35%，如AI生成内容的准确性）、“数据隐私”（34%，如客户数据是否加密）、“可靠性”（32%，如服务是否稳定不宕机）是Top3优先级，“成本”（25%）反而位居其后。显示，“适配性”（38%）——即技术能否贴合自身业务场景（如客服效率低、生产良率差）——成为首要考量，其次是“可扩展性”（32%，未来能否支撑业务增长）和“兼容性”（22%，能否与现有系统对接），而单纯的“技术先进性”仅占8%。另有企业因“客户数据未加密”导致泄露，面临用户索赔。
博客
视频：2025年全球机器人产业发展白皮书-具身智能时代的技术突破|附39份报告PDF、数据、可视化模板汇总下载
12-05 47
2025年，这场以AI大模型为核心的产业革命，已形成“技术突破-生态集聚-场景落地”的闭环，中国通过“制造业底座+区域生态+政策赋能”的核心路径，成为全球具身智能规模化落地的关键战场。在3C电子场景，精密涂胶、PCBA上下料检测等任务的自动化率已达60%，成为场景落地的标杆。整机厂商牵头整合技术，核心部件供应商突破硬件瓶颈，场景企业提供真实数据与落地场景，三方协同推动产品迭代，如富临精工与智元机器人合作，实现周转箱拆垛上料任务的24小时不间断作业，单班完成800余个周转箱搬运，全程零失误。
博客
Python主题建模、情感分析酒店评论、工商银行手机APP用户评论：MLP、LSTM、CNN、LDA、SVM、朴素贝叶斯
12-05 431
为此，我们构建了一套“文本预处理-特征提取-主题挖掘-多模型分类”的完整解决方案，基于ChnSentiCorp中文酒店评论数据集，整合TF-IDF特征提取、LDA主题建模与9种主流机器学习/深度学习模型，既实现了情感倾向的精准分类，又挖掘出差评背后的核心问题。移动互联网的普及让手机银行成为金融服务的核心载体，用户在使用过程中留下的海量评论，藏着对服务的真实反馈和潜在需求。“好”“服务”“非常”“方便”等词汇的TF-IDF分数最高，说明这些词汇在正面评论中出现频率高且具有独特性，是区分正面情感的关键指标。
博客
2025医疗健康行业革新报告：AI赋能、国际化|附170+份报告PDF、数据、可视化模板汇总下载
12-05 182
65岁以上群体从67%降至60%，是所有年龄组中降幅最大的群体之一。2024年中国医疗器械出口产品结构中，医疗设备（43.6%）、医用耗材（38.0%）、IVD试剂（10.5%）、IVD仪器（3.3%）构成主要品类，其中影像设备、麻醉机、监护仪等中高端设备出口增速超20%，反映产品结构持续升级。中国医疗大模型已在多场景实现规模化应用，其中医疗服务（医学影像、智能诊疗）渗透率11.0%，医院管理（质量管理、设备管理）渗透率10.1%，健康管理与医学科研渗透率13.0%，形成“诊疗为核、管理协同”的应用格局。
博客
专题：2025年全球机器人产业发展白皮书-具身智能时代的技术突破|附39份报告PDF、数据、可视化模板汇总下载
11-26 102
2025年，这场以AI大模型为核心的产业革命，已形成“技术突破-生态集聚-场景落地”的闭环，中国通过“制造业底座+区域生态+政策赋能”的核心路径，成为全球具身智能规模化落地的关键战场。在3C电子场景，精密涂胶、PCBA上下料检测等任务的自动化率已达60%，成为场景落地的标杆。整机厂商牵头整合技术，核心部件供应商突破硬件瓶颈，场景企业提供真实数据与落地场景，三方协同推动产品迭代，如富临精工与智元机器人合作，实现周转箱拆垛上料任务的24小时不间断作业，单班完成800余个周转箱搬运，全程零失误。
博客
Python新能源电动汽车NEV数据故障预警：动态采样、随机森林、XGBoost、决策树集成模型分析|附代码数据
11-26 396
文章围绕新能源电动汽车故障等级判断核心需求，依次完成了数据预处理（差异化缺失值填充、多维度异常值修正）、特征分析（Spearman相关系数、卡方检验、随机森林特征重要性筛选）、模型构建（随机森林、XGBoost、决策树的袋装集成模型，结合三级协同策略处理类不平衡问题）、10月故障等级预测及用车策略制定等工作。作为数据科学团队，我们曾承接某新能源车企的车辆故障预警咨询项目，基于实际运营的电动汽车9个月运行数据，搭建了一套从数据清洗到模型部署的全流程故障预警方案，本文正是该项目的技术沉淀与成果拆解。
博客
专题：2025-2026医药健康行业消费趋势白皮书：数字化全景洞察|附180+份报告PDF、数据可视化模板汇总下载
11-26 403
搭建数字化用户需求调研体系，聚焦本地核心消费人群的健康数字化痛点（如年轻群体的情绪养生数字化方案、老年群体的适老化数字化产品），结合报告数据优化产品数字化定位，领取《数字化用户需求调研模板》可快速落地。报告将从数字化消费趋势、心理健康数字化关怀、智慧养老数字化落地、环境健康技术赋能、AI数字化重构生态五大维度，拆解行业数字化转型的机遇与挑战，为创业者、品牌方、从业者提供可落地的数字化决策参考。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值