实时渲染(第三版):第四章 转换 4.1.5, 4.1.6, 4.1.7, 4.1.8

 

4.1.5 转换串联

    由于矩阵乘法的不可交换性，矩阵操作的顺序至关重要，转换的串联因此是顺序相关的。

    顺序依赖的一个例子，假设有两个矩阵S和R。S(2,0.5,1)执行缩放，Rz(π/6)绕着z轴逆时针旋转π/6弧度。这两个矩阵可以用两种方式相乘，而结果会完全不同，如图4.4所示。

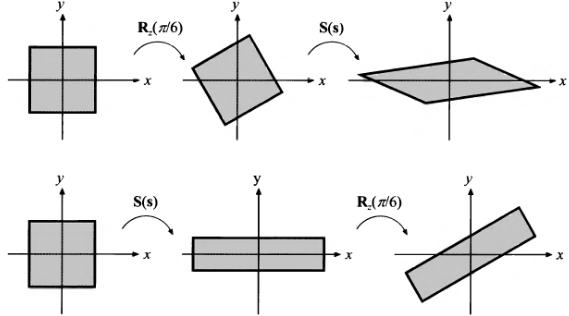
图 4.4 矩阵相乘的顺序相关性示例。上方的一行，首先应用Rz(π/6)，然后是S(s)。它的复合矩阵于是为S(s)Rz(π/6)。下方的一行，则使用相反的顺序，复合矩阵是Rz(π/6)S(s)。两者的结果显然不同。这也说明，通常，对任意矩阵M和N，MN != NM（当然，也有特殊情况，但它们就不是任意矩阵了）。

    将多个转换矩阵串联起来成为一个转换矩阵，其明显的原因是提高效率。比如，想想一个对象，拥有上千个顶点，而这个对象必须被缩放、旋转和平移。在串联之前，我们需要将三个转换矩阵依次和顶点相乘；而串联之后，我们仅需将串联后的单个矩阵和顶点相乘。串联后的复合矩阵为C =TRS。此处，需要注意一下顺序：缩放矩阵S需要首先应用到顶点，因此出现在公式的最右边。和顶点的具体应用为：TRSp = (T(R(Sp)))（在计算机图形学中，另一种有效的符号方案是使用矩阵底部的行作为平移向量。在这种方案中，矩阵的顺序将刚好相反。此方案中的向量和矩阵被叫做行格式，因为向量都是一行一行。本书中，我们使用列格式）。

    矩阵串联是顺序相关的，但值得注意的是，矩阵可以按需编组。比如说，你想要用TRSp计算一次刚体运动转换TR。那么，上段中的公式TRSp = (T(R(Sp)))可以编组为TRSp = (TR)(Sp)。其实，也就是说，这个运算是满足结合律的。

4.1.6 刚体转换

    当某人抓起一个固体对象，比如说桌上的一直笔，并将它移动到另外一个位置，比如说衣服的口袋中，那么，只有对象的朝向和位置发生了改变，而形状通常不收影响。这个转换，仅由平移和旋转串联而成，被叫做刚体转换，拥有保留对象长度、角度和次序（handedness，手性）。

    任何刚体矩阵X，都可写作一个平移矩阵T(t)和一个旋转矩阵R的串联，可表示为公式4.14：

    X的逆计算为X^-1 = (T(t)R)^-1 =R^-1T(t)^-1 = R^TT(-t)。于是，为计算逆矩阵，需要转换R左上3*3，并改变T平移值的符号；然后将得到的两个新矩阵反序相乘。另外一种计算X的逆的方法是如下考虑R（使R成为3*3矩阵）和X：

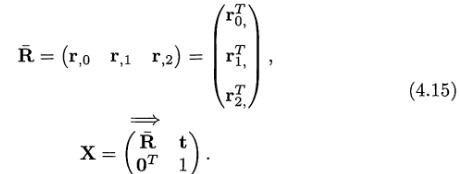
    此处，0是3*1的列向量，其各个部分都是0。用下面表达式中的一些简单的计算就可产生X的逆：

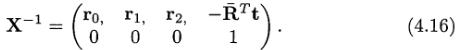
4.1.7 法线转换

    可以使用一个单独的矩阵一致地完成点、线、多边形和其他几何图形的转换。同样的矩阵还能够转换这些线和多边形表面的正切向量。但是，有一个重要的几何属性，该矩阵并不是总能转换，该几何属性便是表面法线（还有顶点光照法线）。图4.5显示了使用同一个矩阵时发生的情况。

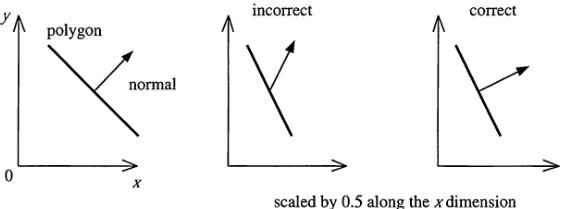
图 4.5 左边是原始的几何图形，一个多边形及其法线。中间显示的是经过x轴缩放后的模型。右侧显示的是正确的法线转换。

    正确的方法是使用共轭矩阵(伴随矩阵)的转置矩阵，而不是原矩阵。共轭矩阵的计算方法在节A.3.1中介绍。共轭矩阵总是存在。在转换之后，法线可能不是单位长度，因此，通常需要标准化一下。

    对转换法线的传统回答是计算逆转矩阵。该方法通常可以行得通，但是完全的逆是不必要的，并且偶尔还无法创建。逆矩阵是共轭矩阵被原矩阵行列式相除的结果。如果行列式值是0，则矩阵是退化矩阵（降秩矩阵），此时，它的逆是不存在的。

    即使仅计算完整4*4矩阵的共轭矩阵，也可能是高代价的，通常也不必要。因为法线是一个向量，因此，平移不会影响到它。进一步讲，大多数模型转换都是仿射的，它们不会改变传入的同质坐标，w部分，如，它们不会执行投影。在这些（通常）情况下，法线转换所需的，是计算左上3*3部分的共轭矩阵。

    即使该共轭矩阵的计算，经常也是不需要的。假设我们知道转换矩阵完全由平移、旋转和统一缩放（没有拉伸或挤压）串联。平移不会影响法线。统一缩放只是简单地改变了法线的长度。那么，剩下的只是一系列的旋转，而旋转也就那么几种类型。旋转矩阵的定义，有那么一个事实，即它的转置就是它的逆。逆转可被用来转换法线，而两个转置或两个逆则互相抵消。把这些放到一起，最终的结果是，在这些条件下，原始的转换矩阵自身就可以直接用来转换法线。

    最后，并不总是必须完全重新标准化生成的法线。如果只有平移和旋转串联，则法线的长度就不会改变，此时就无需重新标准化。如果统一缩放被串联，则可使用整体缩放因子（如果知道的话，否则就提取，参考节4.2.3）直接标准化。比如，如果我们知道一系列缩放最终使对象变大为5.2倍，那么，我们就可以将生成的法线向量直接除以5.2。另外，为创建可以生成标准化结果的法线转换矩阵，可以将原矩阵左上3*3的部分除以该整体缩放因子。

    注意，在转换后表面法线来自三角形（如使用三角形边的叉积）的系统中,法线转换不是一个问题。正切向量在性质上和法线不同，总是可以直接使用原矩阵进行转换。

4.1.8 逆计算

    许多情况需要用到逆矩阵，比如，要在坐标系统间来回改变。可以使用下面的方法计算不同类型的转换矩阵的逆：

• 如果矩阵执行的是一个单独的转换，或者是一系列指定参数的简单转换，则可简单地使用“逆参数”和逆矩阵顺序的方法进行计算。如，如果M = T(t)R(Φ)，则M^-1 = R(-Φ)T(-t)。
• 如果矩阵是正交的，则M^-1 = M^T。任何旋转序列都是一个旋转，因此是正交的。
• 如果不知道矩阵的任何信息，则可使用共轭方法（公式A.38）、克拉马法则、LU分解或高斯消去等进行计算。通常可以选用共轭方法和克拉马法则，因为它们的分支操作很少；在现代架构上，避免if测试是好的。对于如何使用共轭以逆转换法线，可以参考节4.1.7。

    在优化时也可以考虑逆计算的目的。比如，如果用来转换向量，那么只要计算矩阵左上3*3的部分的逆（参考前节）。