数据结构值排序算法（三）-快速排序

基本思想：

快速排序采用的思想是分治思想。

第一趟排序：快速排序是找出一个元素（理论上可以随便找一个）作为基准(pivot),然后对数组进行分区操作,使基准左边元素的值都不大于基准值,基准右边的元素值 都不小于基准值，如此作为基准的元素调整到排序后的正确位置。

递归排序：第二步就是对高段位和地段为两部分进行递归排序。

一趟快速排序的算法的步骤是：
1）设置两个变量low、high，排序开始的时候：low=0，high=N-1；
2）以第一个数组元素作为关键数据，赋值给key，即key=A[0]；
3）从high开始向前搜索，即由后开始向前搜索(high--)，找到第一个小于key的值A[high]，将A[high]和A[low]互换；
4）从i开始向后搜索，即由前开始向后搜索(low++)，找到第一个大于key的A[low]，将A[low]和A[high]互换；
5）重复第3、4步，直到low=high；

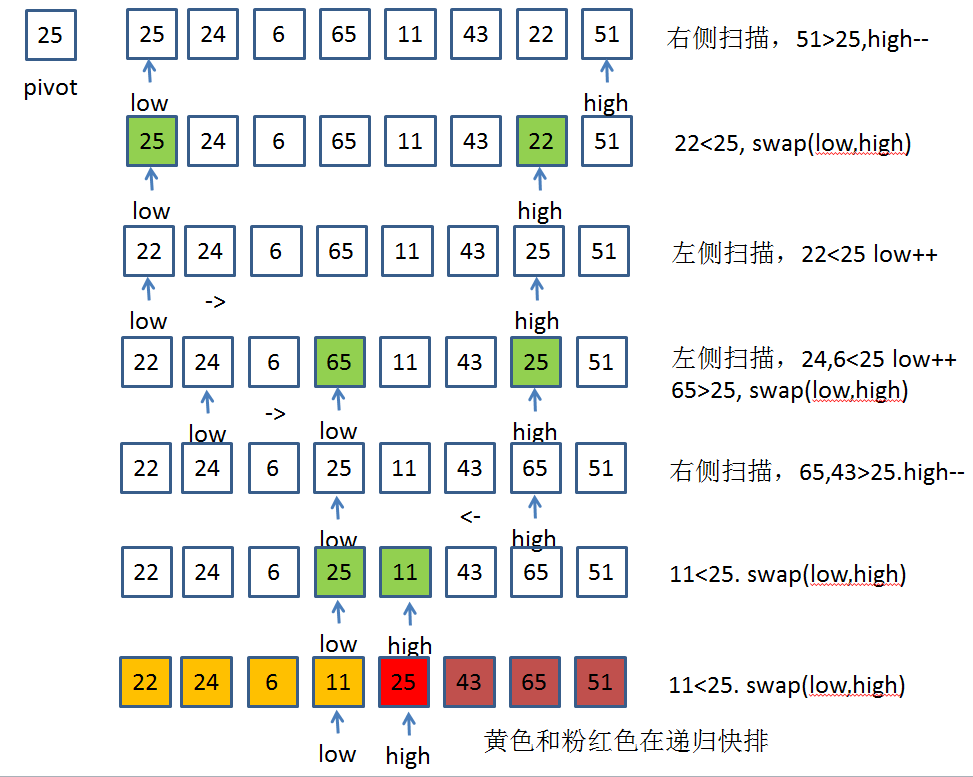
一趟快速排序的算法的图解是：

QuickSortClass.java

public class QuickSortClass {
   private int[] array;

   public int[] getArray() {
	   return array;
   }

   public void setArray(int[] array) {
	   this.array = array;
   }
   //快速排序  
   public void quikSort(){  
       QuikSort(0,array.length-1);  
   }  
 
   //递归的快速排序 
   private void QuikSort(int low,int high){  
       if(low>=high){  
              return;  
       }else{  
              int pivot = array[low];  //以第一个元素为基准  
              int partition =partition(low,high,pivot);  //对数组进行划分，比pivot小的元素在低位段，比pivot大的元素在高位段  
              
              QuikSort(low,partition-1);   //对划分后的低位段进行快速排序  
              QuikSort(partition+1,high);  //对划分后的高位段进行快速排序  
       }  
   }  
 

   //以pivot为基准对下标low到high的数组进行划分 ,low 数组段的最小下标 ,high 数组段的最大下标 , pivot 划分的基准元素 , 划分完成后基准元素所在位置的下标 
   private int partition(int low,int high,int pivot){  
        
       while(low<high){               
              while(low<high &&array[high]>=pivot){  //从右端开始扫描，定位到第一个比pivot小的元素  
                     high--;  //如果array[high]比基准pivot大，就不管，继续向前移动
              }  
              swap(low,high);  //如果array[high]比基准pivot小，就交换low和high
               
              while(low<high &&array[low]<=pivot){  //从左端开始扫描，定位到第一个比pivot大的元素  
                     low++;    //如果array[low]比基准pivot小，就不管，继续向后移动
              }  
              swap(low,high);  //如果array[low]比基准pivot大，就交换low和high 
               
       }  
       return low;  
        
}  
   //交换数组中两个元素的数据 
   private void swap(int low,int high){  
       int temp = array[high];  
       array[high] = array[low];  
       array[low] = temp;  
   }  
}

TestQuickSort.java

public class TestQuickSort {
	public static void main(String[] args) {
		// TODO Auto-generated method stub
       int[] list={25,24,6,65,11,43,22,51};
       QuickSortClass qs=new QuickSortClass();
       System.out.println("快排前的数组是：");
       for(int i=0;i<list.length;i++){
    	   System.out.print(list[i]+" ");
       }
      qs.setArray(list);
      qs.quikSort();
      int[] list2= qs.getArray();
       System.out.println();
       System.out.println("快排后的数组是：");
       for(int i=0;i<list2.length;i++){
    	   System.out.print(list2[i]+" ");
       }
	}
}

算法分析：

在最差的情况下，划分有n个元素构成的数组需要进行n次比较和n次移动，因此划分所需的时间为O(n).在最差的情况下，每次主元会将数组划分成为一个大数组和一个空数组。这个大数组的规模是在上次划分的基础上减一。该算法需要(n-1)+(n-2)+...+2+1=O(n2).

在最佳的情况下，每次主元会将数组划分成为规模大致相等的部分。设T(n)标识使用快速排序算法堆包含n个元素的数组排序所需要的时间，因此

                        T(n)=T(n/2)+T(n/2)+n

快速排序的T(n)=O(nlogn)