2.7 特征分解

声明：该文章翻译自MIT出版的《DEEP LEARNING》，博主会定期更新文章内容。由于博主能力有限，中间有过错之处希望大家给予批评指正，一起学习交流。

许多数学对象分解为一些组成成分后可以更好的理解，或者是找到它们普遍存在的性质，而这些性质不受限于我们选择的表达方式。

例如，整数可以分解成质因子。数字12的表达方式取决于采用二进制还是十进制，但是 $12=2\times2\times3$ 是永远成立的。从这个表示中，我们可以总结出一些有用的性质，例如12不能被5整除，或者12的整数倍都能被3整除。

我们通过分解整数为质因子可以发现它的真实性质，同样的我们可以分解矩阵，得到它们功能性质的一些信息。

最广泛使用的矩阵分解是特征分解，也就是将矩阵分解为一系列特征向量和特征值。

方阵 $\boldsymbol{A}$的特征向量是一个非零向量 $\boldsymbol{v}$，这样的话乘以 $\boldsymbol{A}$仅仅改变 $\boldsymbol{v}$的尺度:

$$\boldsymbol{Av}=\lambda\boldsymbol{v}$$ 标量 $\lambda$是对应特征向量的特征值。（有时候也会发现左特征向量即 $\boldsymbol{v^{\rm T}A}=\lambda\boldsymbol{v}$，但是我们通常关注右特征向量）。

注意如果 $\boldsymbol{v}$是 $\boldsymbol{A}$的一个特征向量，那么任何缩放向量 $s\boldsymbol{v}$也是特征向量，其中$s\in {\rm R},s\neq0$。而且，依然有相同的特征值。因此，我们通常只寻找单位特征向量。
我们可以用特征分解来表示矩阵 $\boldsymbol{A}$,特征向量为${\boldsymbol{v^{(1)},...,v^{(\rm n)}}}$对应的特征值为 ${\lambda_{(1)}},...,\lambda_{(n)}$，特征分解就是级联特征向量到矩阵 ${\boldsymbol{V}=\{\boldsymbol{v^{(1)},...,v^{(\rm n)}}}\}$，级联特征值到向量 $\boldsymbol{\lambda}$。因此，矩阵

$$\boldsymbol{A=V{\rm diag}(\lambda)V^{(-1)}}$$ 具有需要的特征值和特征向量。如果 $\boldsymbol{V}$是正交矩阵，那么我们可以将 $\boldsymbol{A}$看做是在 $\boldsymbol{v^{(i)}}$方向上缩放 $\lambda_i$倍。如下图

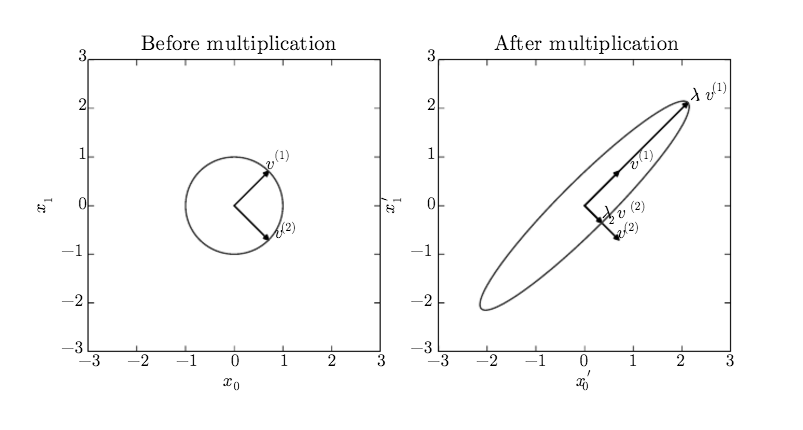
我们已经看到，构建具有特定特征向量和特征值的矩阵可以在所需的方向上伸展空间。然而，我们经常将矩阵分解到他们的特征向量和特征值上。这样做可以帮助我们分析矩阵的某些性质，正如分解一个整数到它的质因子可以帮助我们认识到整数的行为一样。

不是每个矩阵都可以分解成特征值和特征向量。在一些情况下，即使分解存在，但可能涉及复数而不是实数。幸运的是，在这本书中，我们通常只分解一种特定的矩阵，该类矩阵有一个简单的分解。具体来说，每个实对称矩阵分解成只用实值特征向量和特征值构成的表达式：

$$\boldsymbol{A=Q\Lambda Q^{\rm T}}$$ 其中 $\boldsymbol{Q}$是由矩阵的特征向量构成的正交矩阵，并且是一个对角矩阵。特征值 $\Lambda_{i,j}$和 $\boldsymbol{Q}$ 的第 $i$列特征向量(用 $\boldsymbol{Q_{:,i}}$表示)有关。

虽然实对称矩阵A保证有一个特征分解，但特征分解不是唯一的。如果任何两个或更多个特征向量共享同一个特征值，那么在正交向量空间中的向量也是特征向量对应的特征值，我们可以用这些特征向量等同地选择一个 $\boldsymbol{Q}$值。按照惯例，我们通常对 $\Lambda$进行降序排列。根据这一惯例，特征分解是唯一的仅当所有的特征值是唯一的时候。

矩阵的特征值分解告诉我们许多有用的事实。矩阵是奇异的当且仅当特征值都是0。特征分解也可用于优化形如 $f(\boldsymbol{x})=\boldsymbol{x^{\rm T}Ax}$服从$\Vert x\Vert_{2}=1$的二次表达式。$\boldsymbol{x}$等于 $\boldsymbol{A}$的特征向量，$f$ 表示对应特征值的数值。约束区域内 $f$的最大值是最大特征值，约束区域内 $f$的最小值是最小特征值。

特征值都是正的矩阵被称为正定。特征值均为正数或零的被称为半正定。同样地，如果所有的特征值是负的，矩阵是负定的，如果所有特征值是负的或零，它是半负定。半正定矩阵非常有趣，因为他们保证 $\forall\boldsymbol{x,x^{\rm T}Ax}\geq0,$。正定矩阵额外保证$\boldsymbol{x^{\rm T}Ax}=0\Rightarrow\boldsymbol{x}=0$。