从正整数 0,1,2,3,… 开始,然后加入负整数和非整的有理数,通过往有理数中加入所有有理数的非有理极限即可获得实数系。例如,无理数 2√ 就是增(或单调(monotone))序列 xn 的极限,其中 x2n<2 且 xn 是有理数,或者用 1,1.4,1.414,… 这样的小数序列表示, 2√ 不是有理数这个事实已经广为人知,而欧几里得首先证明了这个事实。
接下来问题来了,我们如何用正式的方式来执行上面的过程呢?实际上,这个过程有点长但是不难,所以我们在这里只给出一个大纲。要做的第一件事就是将那些我们希望实数具有的重要性质隔离掉,如下所示:
(I)
加法公理。有一个加法运算“+”使得对于所有数
x,y,z
,满足
1.
x+y=y+x
(交换性)
2.
x+(y+z)=(x+y)+z
(结合性)
3. 有一个数0使得
x+0=x
(存在零元)
4. 对于每个
x
,有一个数
(II)
乘法公理。有一个乘法运算“
⋅
”使得
1.
x⋅y=y⋅x
(交换性)
2.
x⋅(y⋅z)=(x⋅y)⋅z
(结合性)
3. 有一个数
1≠0
使得
1⋅x=x
(存在单位元)
4. 对于每个
x≠0
,存在一个数
v
使得
5.
x⋅(y+z)=x⋅y+x⋅z
(分配律)
(III)
有序公理。有一个序“
≤
”(更精确点,一种关系)使得
1.
x≤y,y≤z
,那么
x≤z
(传递性)
2.
x≤y,y≤x⇔(x=y)
(自反性)
3. 对于任意两个元素
x,y
,要么
x≤y
,要么
y≤x
(三分性)
4. 如果
x≤y
,那么
x+z≤y+z
5.
0≤x,0≤y
那么
0≤xy
任何集合或数系,如果他们具有满足加法公理和乘法公理的运算+和 ⋅ ,那么我们称之为域(field)。例如,有理数是一个域但整数不是。
满足性质
(I),(II),(III)
的称为有序域,根据定义,
x<y
意味着
x≤y
且
x≠y
,其他大家熟悉的符号也可以引进来,例如数
x
的大小是
利用这些公理就可以推出从高中开始学到的运算法则,例如我们可以用公理来证明 0<1 ,上面公理完整的细节对我们目前的工作不重要,所以我们不加证明的接受这些事实,就当成我们平常熟悉的代数法则。
很明显,要想唯一地表征实数,上面的公理是不充分的,因为有理数也满足这些公理,所以我们需要另一个条件来确保有理数的极限包含在实数系中。
为了陈述这个条件,需要介绍一些与序列相关的定义。令
xn
表示给定的数列,如果对于任意
ε>0
,存在一个正数
N
,使得对于所以
直观上讲,收敛就是当
n
充分大时,
对于所有
不难看出序列
xn
顶多收敛到一个点,假设
xn
收敛到
x,y
,那么根据三角不等式
|x−y|=|x−xn+xn−y|≤|x−xn|+|xn−y|
,如果
|x−y|>0
,那么将
|x−y|/2
作为
ε
,我们可以选择充分大的
N
使得当
现在我们陈述完备性公理。
(IV)
1. 完备性公理。如果
xn
是增序列且有上界,那么
xn
收敛到某个数
x
。
对于条件
满足公理 (I) 到 (IV) 的数系叫做全序域(complete ordered field)。条件 (IV) 和有下界的减序列收敛这个条件是等价的,通过观察 (xn→x) ⇔ (−xn→−x) 即可明白这个条件,现在我们结合前面的讨论给出下面的定理。
定理1 存在唯一的一个全序域数系,我们称之为实数系。
实数系用
R
表示,目前
正如上面所说的,我们不希望花太多时间来了解所有公理结论的细节,但是一些显然的结论还是值得特别关注的,即阿基米德性(Archimedian property):给定任意实数
完备性公理可以表示成其他非常重要的等价形式,为了陈述这些形式,我们需要一些基本的术语。
定义1
令
S⊂R
是
R
的一个子集,那么
如果
b
不但是
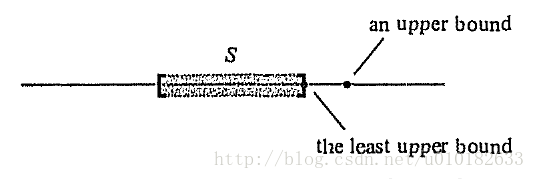
图1
集合
[a,b]={x∈R|a≤x≤b}
叫做闭区间(closed interval)。
例如,闭区间[0,1],开区间(0,1)和所有小于1的有理数最小上界都是1。
注意:
S
的最小上界(也叫做
S
最多有一个最小上界。如果
集合不一定有上界,例如整个实数系就没有上界,而且正整数也没有上界,考虑退化的情况即空集 ∅ ,我们将任何数都看成它的上界。
通过观察可以看出如果
b
是
最小上界的定义有另一个非常有用的陈述,即定理2,有时候应用定理2会更加方便。
定理2
令
S⊂R
,当且仅当
b
是
这个定理直观上非常明显,因为
如果
S
没有上界,我们就说
我们需要的另一个符号是柯西序列(Cauchy sequence)。
定义2
对于
R
中的一个序列
这个条件直观上意味着序列会聚成一团;也就是序列的所有元素在序列的充分远处互相之间会任意的接近。
如果
xn
收敛到
x
,那么
定理3
1. 令
S
是
2. 令
P
是
3.
R
中的每个柯西序列
这个结果非常明显。实际上,如果
R
的有界子集没有最小上界,那么集合顶部将会有一个洞并且
利用我们给出的证明方法,不难看出条件
这里我们简要的回顾并讨论了实数轴,接下我们给出一些具体实例。
例1: 令 S=x∈R|x2+x<3 ,求出 sup(S),inf(S) 。
解:
考虑
y=x2+x
的图像,利用基本的微积分知识可知在
x=−1/2
处,
y
取最小值,所以
可得
例2: 令 x0=0,x1=2√,x2=2+x1−−−−−√,…,xn=2+xn−1−−−−−−−√,… ,说明 xn 收敛。
解:
我们将说明
xn
是递增且有上界,这样就证明了该断言。注意每个
xn
是非负的,那么我们必须说明
rn=xn+1−xn≥0
,这里用归纳法证明。当
n=0
时明显成立,假设
n−1
时成立,那么
所以
rn−1≥0
意味着
rn≥0
,因此
xn
是递增的。接下来我们要说明
xn
有上界,例如我们可以用归纳法证明
xn∗≤5
。显然,
x0,x1≤5
,假设
xn−1≤5
,那么
因此
xn
是递增且有上界,所以它是收敛的。
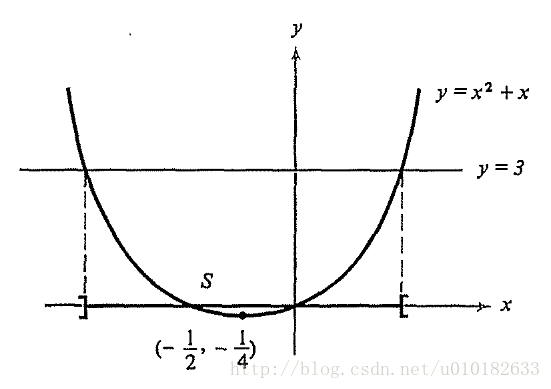
图2
例3: 令 xn 是实数序列,且满足 |xn−xn+1|≤1/2n ,说明 xn 收敛。
解:
我们将说明
xn
是柯西序列,那么利用条件
(iii)
即可得到结果。利用三角不等式可得
(因为如果 0<r<1 ,那么 a+ar+ar2+⋯=a/(1−r) )。
因此如果
m≥n
并且给定
ε>0
,只选择使
1/2N−1<ε
的
N
,那么
例4: 证明当 n→∞ 时 1/n→0 。
解:
根据定义,给定任意数
ε>0
,我们必须证明有一个整数
N
使得如果
例5: 说明当 n→∞ 时 n2+1√n!→0 。
解:
我们必须说明当
n
充分大时,
所欲给定
ε>0
,选择
N
使其
这就证明了断言。
例6是出自公理的代数法则,在实际中,像这样的结论我们都认为是理所当然的。
例6:
利用有序域的公理证明
1. 负元是唯一的;
2. 对所有
x,0x=0
;
3.
(−x)(−y)=xy
;
4.
0<1
解:
对于
(a)
,我们注意到如果
x+w=0,x+y=0
,那么(
y
加到
对于 (b) ,我们有0+0=0,所以利用 II(i),II(v) 我们得到 0⋅x=(0+0)x=0⋅x+0⋅x ,两边都加上 −(0⋅x) 得 0⋅x=0 。
对于
(c)
我们首先说明
(−x)y=−(xy)
。事实上,根据
II(i),II(v)
,
(−x)y+xy=(−x+x)y=0⋅y=0
(
(b)
),接下来,因为
(1−1)(−1)=0
并且
(1)(−1)+(−1)(−1)=−1+(−1)(−1)
,两边分别加1可得
(−1)(−1)=1
,因为我们已经证明了
(−1)(x)=−(1x)=−x
,所以
最后,对于 (d) ,根据 III(iii) 0<1 的其他可能只有 1≤0 ,两边加-1得到 0≤−1 (利用 III(iv) ),那么 x=−1,y=−1 将得出 0≤1 ( III(v) ),因为 0≠1 ,所以我们有 0<1 。





















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








