RMQ(Range Minimum Query)

最新推荐文章于 2022-03-29 12:43:01 发布

GatsbyNewton

最新推荐文章于 2022-03-29 12:43:01 发布

阅读量1.3k

点赞数

分类专栏： Machine Learning 文章标签：算法

本文链接：https://blog.csdn.net/u010376788/article/details/78010389

版权

Machine Learning 专栏收录该内容

11 篇文章 2 订阅

订阅专栏

RMQ

RMQ（Range Minimum Query） 是指区间最值查询，即对于长度为 $n$ 的数列 $A$ ，回答若干询问 $RMQ(A, i, j), (i,j <= n)$ ，返回数列 $A$ 中下标在 $i, j$ 之间的最小/大值。如果用 $f(n)$ 表示算法预处理时间复杂度， $g(n)$ 表示算法的查询时间复杂度，那么 RMQ 的算法的复杂度是 $\left \langle f(n), g(n) \right \rangle$

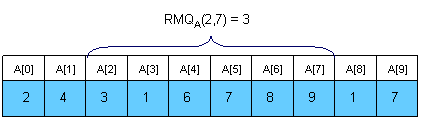
解决 RMQ 有三种方法：
1. 普通动态规划；
2. Sparse Table（ST）；
3. Segment Tree（线段树）。

普通动态规划

用 $dp[i][j]$ 表示 $A$ 数列在区间 $\left [ i, j \right ]$ 的最小值的下标索引，算法的复杂度是 $\left \langle O(N^{2}), O(1) \right \rangle$ 那么有：

M [i] [j] = {M [i] [j - 1], j, A [M [i] [j - 1]] < A [j] A [M [i] [j - 1]] ⩾ A [j] .

$M[i][j] = \begin{cases} M[i][j - 1], & A[M[i][j - 1]] < A[j] \\ j, & A[M[i][j - 1]] \geqslant A[j] \end{cases}.$

算法实现

/**
 * @param dp 存储 [i, j] 区间最小值的下标索引
 * @param A
 * @param length 数组长度
 */
public void generaDP(int[][] M, int[] A, int length){
    for (int i = 0; i < length; i++){
        M[i][i] = i;
    }

    for (int i = 0; i < length; i++){
        for (int j = i + 1; j < length; j++){
            M[i][j] = A[M[i][j - 1]] < A[j] ? M[i][j - 1] : j;
        }
    }
}

Sparse Table（ST）

Sparse Table（ST） 也是一种动态规划的方法，需要维护一个二维数组 $M[0, N-1][0, log_{2}N]$ ，其中 $M[i][j]$ 表示在以下标索引 $i$ 开始且长度为 $2^{j}$ 的子数组中最小值的的下标索引。例如：

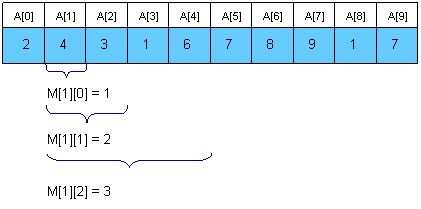
为了计算 $M[i][j]$ ，需要找出

M [i] [j] = {M [i] [j - 1], M [i + 2 j - 1 - 1] [j - 1], A [M [i] [j - 1]] A [M [i + 2 j - 1 - 1] [j - 1]] o t h e r w i s e

$M[i][j] = \begin{cases} M[i][j - 1], & A[M[i][j - 1]] \text A[M[i + 2^{j - 1} - 1][j - 1]] \\ M[i + 2^{j - 1} - 1][j - 1], & otherwise \end{cases}$

算法实现：

/**
 * @param M 存储 [i, j] 区间最小值的下标索引
 * @param A
 * @param length 数组长度
 */
public void sparseTable(int[][] M, int[] A, int length){
    for (int i = 0; i < length; i++){
        M[i][0] = i;
    }

    for (int j = 1; 1 << j <= length; j++){
        for (int i = 0; i + (1 << j) - 1 < length; i++){
            M[i][j] = A[M[i][j - 1]] < A[M[i + (1 << j - 1)][j - 1]] ? M[i][j - 1] : M[i + (1 << j - 1)][j - 1];
        }
    }
}

一旦得到预处理之后的值，就可以计算 $RMQ_{A}\left ( i, j \right )$ 。此时需要有两个能完全覆盖查询区间 $[i, j]$ 的区间块，并且找到最值，算法复杂度是 $\left \langle O(Nlog_{2}N), O(1) \right \rangle$ 。令 $k = log(j - i + 1)$ ，则有：

RMQ_{A}(i, j) = \left\{\begin{matrix}
M[i][k], & A[M[i][k]] \leqslant A[M[j - 2^{k} + 1][k]] \\ 
M[j - 2^{k} + 1][k], & otherwise
\end{matrix}\right.

算法实现：

/**
 * 用 Sparse Table 求 RMQ
 * @param left 查询区间左下标索引
 * @param right 查询区间右下标索引
 * @param M Sparse Table
 * @param A
 */
public void rmqSparseTable(int left, int right, int[][] M, int[] A){
    int k = (int) ( Math.log(right - left + 1) / Math.log(2));
    int rmq = A[M[left][k]] < A[M[right - (int) Math.pow(2, k) + 1][k]] ? M[left][k] : M[right - (int) Math.pow(2, k) + 1][k];
}

Segment Tree（线段树）

RMQ 也可以用 Segment Tree 来解决，其算法复杂度是 $\left \langle O(N), O(logN) \right \rangle$ 。Segment Tree 是一种类堆的数据结构，它可以以对数的时间复杂度进行更新和查询操作。如果定义一个区间 $[i, j]$ ，则有：
1. 第一个节点存储区间 $[i, j]$ 的信息；
2. 如果 $i < j$ ，左右子节点分别存储区间 $[i, \frac{i + j}{2}]$ 和区间 $[\frac{i + j}{2} + 1, j]$ 的信息。

注意：对于 $N$ 个元素的线段树，它的高是 $log_{2}N + 1$ ；需要用一个 $M\left [ 1, 2 * 2^{log_{2}N + 1} \right ]$ 的数组表示线段树。

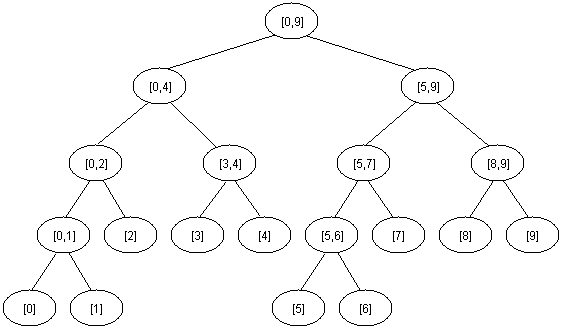
由于 Segment Tree 是一种类堆的数据结构，所以如果有一个非叶子节点 $X$ ，那么它的左子节点是 $2 * X$ ，右子节点是 $2 * X + 1$ 。如果用一个 $M\left [ 1, 2 * 2^{log_{2}N + 1} \right ]$ 的数组表示线段树，其中 $M[i]$ 表示节点 $i$ 对应区间的最值索引。

/**
 * 构建线段树
 * @param node 当前线段树的根节点下标索引
 * @param A 构建线段树的数组
 * @param segmentTree 线段树
 * [begin, end] 构建线段树的数组的起始下标索引
 */
public void buildSegmentTree(int node, int begin, int end, int[] A, int[] segmentTree){
    if (begin == end){
        segmentTree[node] = begin;
    }
    else {
        /**
         * compute the values in the left and right subtree iteratively
         */
        int middle = (begin + end) / 2;
        buildSegmentTree(2 * node, begin, middle, A, segmentTree);
        buildSegmentTree(2 * node + 1, middle + 1, end, A, segmentTree);

        /**
         * search for the minimum value in the first and second half of the interval
         */
        segmentTree[node] = A[segmentTree[2 * node]] <= A[segmentTree[2 * node + 1]] ? segmentTree[2 * node] : segmentTree[2 * node + 1];
    }
}

如果想找到区间 $[i, j]$ 最值的下标索引，可以对构建的 Segment Tree 进行查询：

/**
 * @param node 当前线段树的根节点下标
 * @param A 构建线段树的数组
 * @param segmentTree 线段树
 * [begin, end] 当前节点所在的区间
 * [left, right] 查询区间
 */
public int query(int node, int begin, int end, int left, int rigth, int[] A, int[] segmentTree){
    int p1, p2;

    /**
     * if the current interval doesn't intersect the query interval, return -1
     */
    if (left > end || rigth < begin){
        return -1;
    }

    /**
     * if the current interval is included the query interval, return segmentTree[node]
     */
    if (begin >= left && end <= rigth){
        return segmentTree[node];
    }

    /**
     * compute the minimum position in the left and right part of the interval
     */
    int middle = (begin + end) / 2;
    p1 = query(2 * node, begin, middle, left, rigth, A, segmentTree);
    p2 = query(2 * node + 1, middle + 1, end, left, rigth, A, segmentTree);

    /**
     * return the position where the overall minimum is
     */
    if (p1 == -1){
        return segmentTree[node] = p2;
    }
    if (p2 == -1){
        return segmentTree[node] = p1;
    }
    if (A[p1] <= A[p2]){
        return segmentTree[node] = p1;
    }
    return segmentTree[node] = p2;
}

RMQ

public class RMQ {

    /**
     * @param M 存储 [i, j] 区间最小值的下标索引
     * @param A
     * @param length 数组长度
     */
    public void generalM(int[][] M, int[] A, int length){
        for (int i = 0; i < length; i++){
            M[i][i] = i;
        }

        for (int i = 0; i < length; i++){
            for (int j = i + 1; j < length; j++){
                M[i][j] = A[M[i][j - 1]] < A[j] ? M[i][j - 1] : j;
            }
        }

        System.out.println(M[2][7]);
    }

    /**
     * @param M 存储 [i, j] 区间最小值的下标索引
     * @param A
     * @param length 数组长度
     */
    public void sparseTable(int[][] M, int[] A, int length){
        for (int i = 0; i < length; i++){
            M[i][0] = i;
        }

        for (int j = 1; 1 << j <= length; j++){
            for (int i = 0; i + (1 << j) - 1 < length; i++){
                M[i][j] = A[M[i][j - 1]] < A[M[i + (1 << j - 1)][j - 1]] ? M[i][j - 1] : M[i + (1 << j - 1)][j - 1];
            }
        }
    }

    /**
     * 用 Sparse Table 求 RMQ
     * @param left 查询区间左下标索引
     * @param right 查询区间右下标索引
     * @param M Sparse Table
     * @param A
     */
    public void rmqSparseTable(int left, int right, int[][] M, int[] A){
        int k = (int) ( Math.log(right - left + 1) / Math.log(2));
        int rmq = A[M[left][k]] < A[M[right - (int) Math.pow(2, k) + 1][k]] ? M[left][k] : M[right - (int) Math.pow(2, k) + 1][k];
        System.out.println(rmq);
    }

    /**
     * 构建线段树
     * @param node 当前线段树的根节点下标索引
     * @param A 构建线段树的数组
     * @param segmentTree 线段树
     * [begin, end] 构建线段树的数组的起始下标索引
     */
    public void buildSegmentTree(int node, int begin, int end, int[] A, int[] segmentTree){
        if (begin == end){
            segmentTree[node] = begin;
        }
        else {
            /**
             * compute the values in the left and right subtree iteratively
             */
            int middle = (begin + end) / 2;
            buildSegmentTree(2 * node, begin, middle, A, segmentTree);
            buildSegmentTree(2 * node + 1, middle + 1, end, A, segmentTree);

            /**
             * search for the minimum value in the first and second half of the interval
             */
            segmentTree[node] = A[segmentTree[2 * node]] <= A[segmentTree[2 * node + 1]] ? segmentTree[2 * node] : segmentTree[2 * node + 1];
        }
    }

    /**
     * @param node 当前线段树的根节点下标
     * @param A 构建线段树的数组
     * @param segmentTree 线段树
     * [begin, end] 当前节点所在的区间
     * [left, right] 查询区间
     */
    public int query(int node, int begin, int end, int left, int rigth, int[] A, int[] segmentTree){
        int p1, p2;

        /**
         * if the current interval doesn't intersect the query interval, return -1
         */
        if (left > end || rigth < begin){
            return -1;
        }

        /**
         * if the current interval is included the query interval, return segmentTree[node]
         */
        if (begin >= left && end <= rigth){
            return segmentTree[node];
        }

        /**
         * compute the minimum position in the left and right part of the interval
         */
        int middle = (begin + end) / 2;
        p1 = query(2 * node, begin, middle, left, rigth, A, segmentTree);
        p2 = query(2 * node + 1, middle + 1, end, left, rigth, A, segmentTree);

        /**
         * return the position where the overall minimum is
         */
        if (p1 == -1){
            return segmentTree[node] = p2;
        }
        if (p2 == -1){
            return segmentTree[node] = p1;
        }
        if (A[p1] <= A[p2]){
            return segmentTree[node] = p1;
        }
        return segmentTree[node] = p2;
    }


    public static void main(String[] args){
        RMQ rmq = new RMQ();
        int[] A = {2, 4, 3, 1, 6, 7, 8, 9, 1, 7};
        int[][] matrix = new int[A.length][A.length];
        rmq.generalM(matrix, A, A.length);
        rmq.sparseTable(matrix, A, A.length);
        rmq.rmqSparseTable(7, 9, matrix, A);

        int[] segmentTree = new int[A.length * 4 * 4];
        rmq.buildSegmentTree(1, 0, A.length - 1, A, segmentTree);
        System.out.println(Arrays.toString(segmentTree));
        System.out.println(rmq.query(1, 0, A.length - 1, 2, 7, A, segmentTree));

    }
}

GatsbyNewton

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
RMQ(Range Minimum Query)

RMQRMQ（Range Minimum Query）是指区间最值查询，即对于长度为 $ n $ 的数列 $ A $，回答若干询问 $ RMQ(A, i, j), (i,j <= n) $，返回数列 $ A $中下标在 $ i, j $ 之间的最小/大值。如果用 $ f(n) $ 表示算法预处理时间复杂度，$ g(n) $ 表示算法的查询时间复杂度，那么 RMQ 的算法的复杂度是 $ \left
复制链接

扫一扫