Codeforces Round #315 (Div. 1) B. Symmetric and Transitive 斯特林数 贝尔数

B. Symmetric and Transitive

time limit per test

1.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Little Johnny has recently learned about set theory. Now he is studying binary relations. You've probably heard the term "equivalence relation". These relations are very important in many areas of mathematics. For example, the equality of the two numbers is an equivalence relation.

A set ρ of pairs (a, b) of elements of some set A is called a binary relation on set A. For two elements a and b of the set A we say that they are in relation ρ, if pair 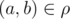, in this case we use a notation .

Binary relation is equivalence relation, if:

1. It is reflexive (for any a it is true that );
2. It is symmetric (for any a, b it is true that if , then );
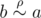3. It is transitive (if  and 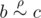, than ).

Little Johnny is not completely a fool and he noticed that the first condition is not necessary! Here is his "proof":

Take any two elements, a and b. If , then 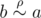 (according to property (2)), which means  (according to property (3)).

It's very simple, isn't it? However, you noticed that Johnny's "proof" is wrong, and decided to show him a lot of examples that prove him wrong.

Here's your task: count the number of binary relations over a set of size n such that they are symmetric, transitive, but not an equivalence relations (i.e. they are not reflexive).

Since their number may be very large (not 0, according to Little Johnny), print the remainder of integer division of this number by109 + 7.

Input

A single line contains a single integer n (1 ≤ n ≤ 4000).

Output

In a single line print the answer to the problem modulo 109 + 7.

Sample test(s)

input

1

output

1

input

2

output

3

input

3

output

10

Note

If n = 1 there is only one such relation — an empty one, i.e. 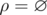. In other words, for a single element x of set A the following is hold: .

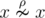If n = 2 there are three such relations. Let's assume that set A consists of two elements, x and y. Then the valid relations are 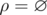,ρ = {(x, x)}, ρ = {(y, y)}. It is easy to see that the three listed binary relations are symmetric and transitive relations, but they are not equivalence relations.

题意，给出n个不同的数，要求二元关系集合（满足交换律 传递律）但不能推出所有的元素都相等的个数。

题目，确实有点拗口。得到的二元关系集合满足交换律如果有 , 那么也存在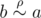，结合律，if  and 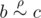, than 。

ans表要求的结果，dp[i][j]把i个不同元素划分成j个非空集合的个数。c[i][j]组合数。

反向思考一个，如果要推出所有的ai = ai,这个问题就简单了。要能推出所有的ai = ai,也就是要求把把i个不同元素划分成j个非空集合的个数。因为，这里我们把一个集合看成一个连通块，这个连通块里，任何两个元素间都有相连的无向边。如3个元素的集合{a, b, c}有3种不同的划分方法：{{a}, {b, c}}, {{b}, {a, c}}, {{c}, {a, b}}，其中{b,c}可以看成{b~c,c~b,b~b,c~c}的集合。把相等的关系转化成了求划分集合的问题。这也是本题的本质。

这样，问题分解成，枚举能推出其的i个相等的元素（i<n 组合c[n,i]），其它n - i个元素都不能推出的个数;也就是sum(c[n][i] * dp[i][i]);这个公式的意思就是随便选i个，再把这i个元素分成i个集合的个数。

c[i,j]是组合数，直接用组合数的关系c[i,j] = c[i-1,j-1] + c[i-1,j]求出。

dp[i,j]是 斯特林数 也是贝尔数用公式也就是贝尔矩阵 dp[i][j] = (dp[i][j-1] + dp[i-1][j-1]);也可以求出。

总的复杂度为O(n*n);

#define N  4005
#define M 100005
#define maxn 205
#define MOD 1000000007
int n;
ll dp[N][N],c[N][N];
int main()
{
    dp[0][0] = dp[1][1] = 1;
    for(int i = 2;i<N;i++){
        dp[i][1] = dp[i-1][i-1];
        for(int j = 2;j<=i;j++){
            dp[i][j] = (dp[i][j-1] + dp[i-1][j-1]) % MOD;
        }
    }
    for(int i = 1;i<N;i++){
        c[i][0] = c[i][i] = 1;
        for(int j = 1;j<i;j++){
            c[i][j] = (c[i-1][j-1] + c[i-1][j]) % MOD;
        }
    }
     while(S(n)!=EOF)
    {
        ll ans = 0;
        for(int i = 0;i<n;i++){
            ans += c[n][i] * dp[i][i];
            ans %= MOD;
        }
        cout<<ans<<endl;
    }
    return 0;
}