机器学习实战——Logistic回归

回归概述（个人理解的总结）

回归是数学中的一种模拟离散数据点的数学模型的方法，拟合一个连续的函数从而可以对未知的离散数据点进行分类或预测。这种方法有一个统一的形式，给定$n$维特征的数据集合，对任意一个数据点$X_i=\{x_i^{(1)}，x_i^{(2)}，...,x_i^{(n)}\}$的每个维度都有一个回归系数$w_i$与之对应，整个模型就存在一个系数向量$w=\{w_1,w_2...w_n\}$。如果是系数向量$w$与特征$X_i$的线性组合，那么就是一个$n$空间下的超平面，如果对应分类问题，那么这个超平面就是分类器的决策平面（分类超平面）。由于线性组合存在常数项，一般为了形式统一，将常数项$b$通过一个$x_0=1$加进系数向量成为$w_0$。
Lotistic回归是经典分类方法，与感知机算法、SVM算法等都是上述的对每个维度的特征进行线性组合，找出决策平面，从而也都是判别式方法。这些方法在训练数据下分别使用不同的决策函数，然后归结为最优化问题，一般使用迭代方法进行，常用的有梯度下降法、牛顿法、拟牛顿法等。

Logistic回归模型

Sigmoid函数

在之前的博客中感知机方法使用的是符号函数$f(x)=sign(x)$，Logistic回归方法使用的是阶跃函数，函数输出的是的两个不同类别的概率值$\{0,1\}$，间断的阶跃函数使用最多的就是Heaviside Step函数，但是不连续的特性对于最优化求解中的求导数不方便。因此使用的是连续的具有阶跃函数相似性质Sigmoid函数：

$$Sigmoid(z) = \frac{1}{1+e^{-z}}$$
该函数定义域为全实数域，任意次连续可微，以点 $（0,0.5）$为对称点。当任意一个输入 $z$很大时函数值趋于1，反之趋于0，在$z=0$时为0.5代表对输入值在两个类别的可能性相当，这些性质是的它非常适合作为分类决策函数。因此，一般当输出值大于或等于0.5时就分类到正类，否则就分到负类。

二分类Logistic模型

分类模型由条件概率$P(Y|X)$表示，其中$Y\in\{0,1\}$代表两个类别，对于给定输入$X=x$：

$$P(Y=1|X=x)= \frac{1}{1+e^{-wx}}$$
$$P(Y=0|X=x)= 1-\frac{1}{1+e^{-wx}}=\frac{1}{1+e^{wx}}$$
其中 $w=\{w_0,w_1.....w_n\},w_0$代表常数项， $x=\{x_0,x_1...x_n\},x_0=1$。对于给定的输入，可以分别求得上述两个概率值，通过比较上述哪个概率值更大，就将输入分到相应类别。也就是Logistic回归模型将特征的线性组合转换为两个类别的概率，线性组合的值越接近于正无穷，概率值越接近1；线性组合的值越接近负无穷，概率值越接近0。
另外，一个事件发生的概率与不发生的概率比值称为几率（odds ratio），取对数之后称为log-odds-ratio，而Logistic回归模型对正类（事件发生）概率和负类（事件不发生）概率的比值如下：
$$log\frac{P(Y=1|X)}{P(Y=0|X)}= \frac{1}{1+e^{-wx}} / \frac{1}{1+e^{wx}}=log(e^{wx})=wx$$
因此，输出Y=1的log-odds-ratio是由输入x的线性函数表示的模型。

模型训练

1.由于是二分类问题，故可认为$P(Y|X)$服从贝努利分布，分布的参数为:

$$\mu(x)= P(Y=1|X=x)= \frac{1}{1+e^{-wx}}$$
第一种解释是从极大似然方法来估计模型的参数，负log似然函数如下：
$$NLL(w)=-log(\prod_{i=1}^N\mu(x_i)^{y_i}*(1-\mu(x)^{1-y_i})) \\= -\sum_{i=1}^N[ y_i log(\mu(x_i))+(1-y_i) log(1-\mu(x_i))]\\=\sum_{i=1}^N \{log(1+e^{wx_i})-y_iwx_i\}$$
这样模型的训练过程就是求解上述目标函数关于参数w的最小值（极大似然在加上负号之后就是最小化），通常使用梯度下降法或者拟牛顿法求解。此处使用梯度下降法，梯度为：
$$\nabla NLL(w_i)= \frac{\partial NLL(w)}{\partial w_i} \\ =(\frac{1}{1+e^{-wx_i}}-y_i)x_i$$
其中的 $\frac{1}{1+e^{-wx_i}}$正好是使用Sigmoid函数得到的 $Y=1$的概率值， $y_i$为第 $i$个样本的类别。根据上述结论既可以使用梯度下降法训练最优的参数$w$，每一步迭代使用上述梯度的反方向更新 $w$。上述$w$的分量形式使用矩阵就为下面的形式：
$$\nabla NLL(w)=X^T\cdot (Y-\frac {1}{(1+e^{X\cdot w})})$$
2.从学习策略角度可以得出和上面一样的结论。学习策略使用的是对数似然损失函数：
$$L(Y,f(X))=-logP(Y|X)$$
从而可以得到经验损失函数：
$$R_{emp}=\frac {1}{N}\sum_{i=1}^N L(Y,f(X))\\=\frac {1}{N}\sum_{i=1}^N-log(\mu(x_i)^{y_i}*(1-\mu(x)^{1-y_i})\\=\frac {1}{N}\sum_{i=1}^N \{log(1+e^{wx_i})-y_iwx_i\}$$
可以看出，上述经验损失函数与之前的极大似然函数形式相同，只有常数系数不同，因此两着在使用梯度下降法求解最优解 $w$是相同的，由此也可以看出极大似然估计等价于学习策略使用对数损失函数下的经验风险最小化。

具体实现

Sigmoid函数

考虑到数据溢出的问题，经过本人反复测试，最终实现的Sigmoid函数实现如下：

def sigmoid(x):
    x = array(x)
    gtIndex = x > 50
    ltIndex = x < -50
    midIndex = gtIndex & ltIndex
    x[gtIndex]  = 1
    x[ltIndex]  = 0
    x[midIndex] = 1.0 / (1 + exp(-1.0 * x[midIndex]))
    return x

因为首先需要计算的是$exp(-x)$这一项，当输入值特别大时，会出现溢出，当时根据函数的性质，可以人为设定当输入值的绝对值大于50时，函数值已经非常接近1或者0，直接进行赋值，同时本人在这里经过反复思考，充分利用了Numpy的索引数组的技巧，同时使用了按位与操作。

训练模型

使用梯度下降法，主要将单个维度的表达式使用矩阵和向量形式表示，从而利用Numpy进行高效计算。

def logisticTrain(ds, labels, stepLen = 1, maxSteps=600, err=80):
    i = 0
    labels = mat(labels).transpose()
    nll = 10 ** 20
    '''Add x_0 and w_0'''
    w    = mat(ones(ds.shape[1] + 1)).transpose()
    data = mat(ones((ds.shape[0], ds.shape[1] + 1)))
    data[:, 1:] = ds
    params = mat(ones(ds.shape[1] + 1)).transpose()

    mingrad = 10 ** 10
    while i < maxSteps:
        ### Negative gradient direction
        grad = data.transpose() * 
               (labels - sigmoid(data * w))
        w = w + stepLen * grad
        deltaGrad = float(grad.transpose() * grad) ** 0.5
        if deltaGrad < mingrad:
            mingrad = deltaGrad
            params  = w
        if deltaGrad < err:
            mingrad = deltaGrad
            params  = w
            break
        i += 1
    return params, deltaGrad, i

其中的提前终止条件使用的是一般最优化方法使用的梯度的二范数，此处我也尝试使用了目标函数值来判断：

def NLL(w, X, y):
    tmp = array(X * w) * array(y)
    return sum(log(1 + exp(X * w)) - mat(tmp))

通过对比当前迭代的w计算的NLL函数值和上一次的差，每次必须保证这个函数值在逐渐减小才行。

模型预测

预测方法比较直接，直接见代码：

def logisticClassify(w, predict):
    p = ones((predict.shape[0], predict.shape[1] + 1))
    p[:,1:] = mat(predict)
    res = sigmoid(p * w)
    res[res >= 0.5] = 1
    res[res < 0.5]  = 0
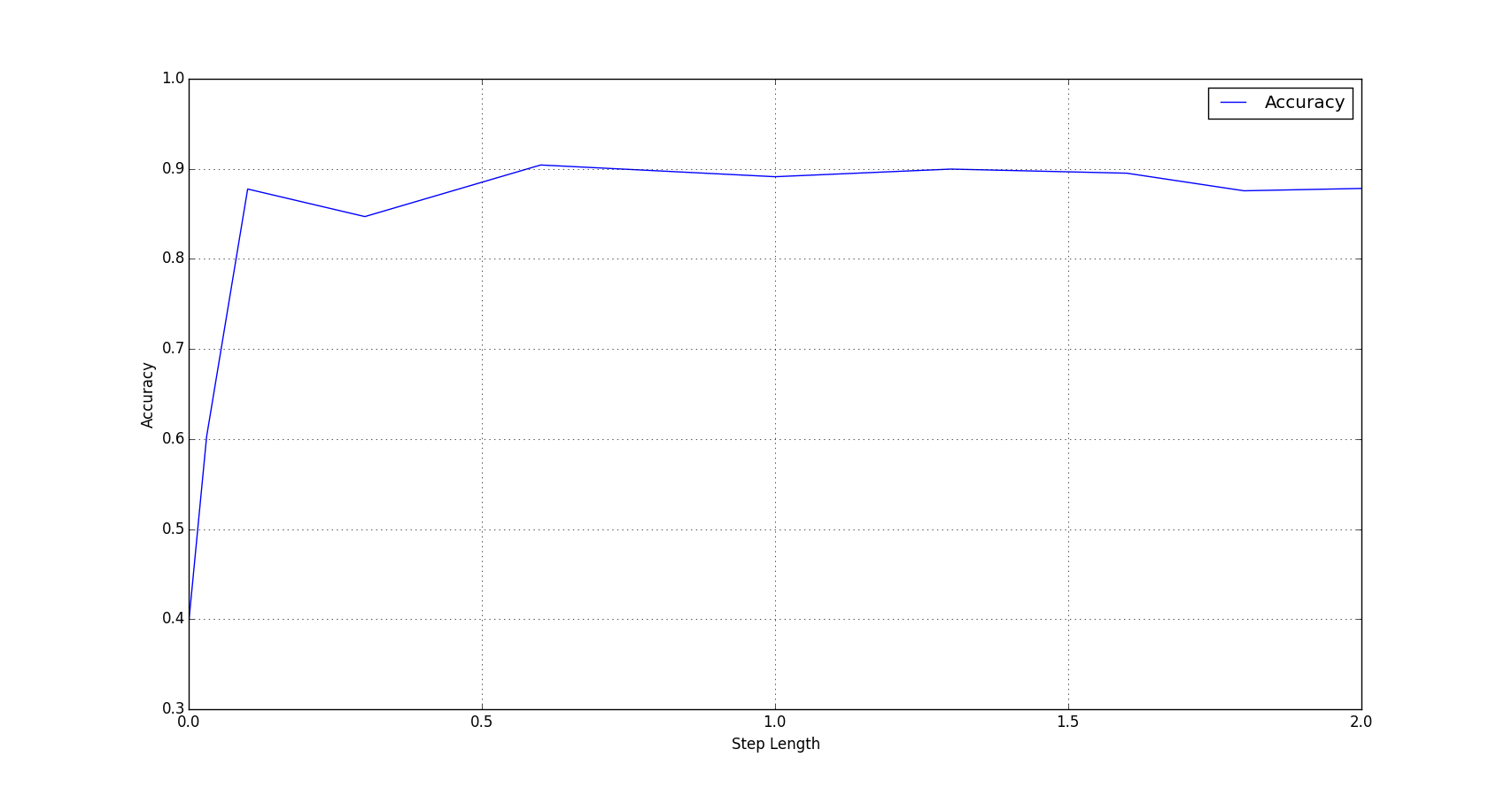
    return res

最终绘制了不同迭代下的步长准确率：