引言
前面我分析了Word2vec的一种模型叫做skip-gram模型。在这篇文章中,我将讲述另一个word2vec模型——连续词袋模型(CBOW)模型。如果你理解skip-gram模型,那么接下来的CBOW模型就更好理解了,因为两者模型互为镜像。我们先来看看CBOW模型与skip-gram模型对比图:
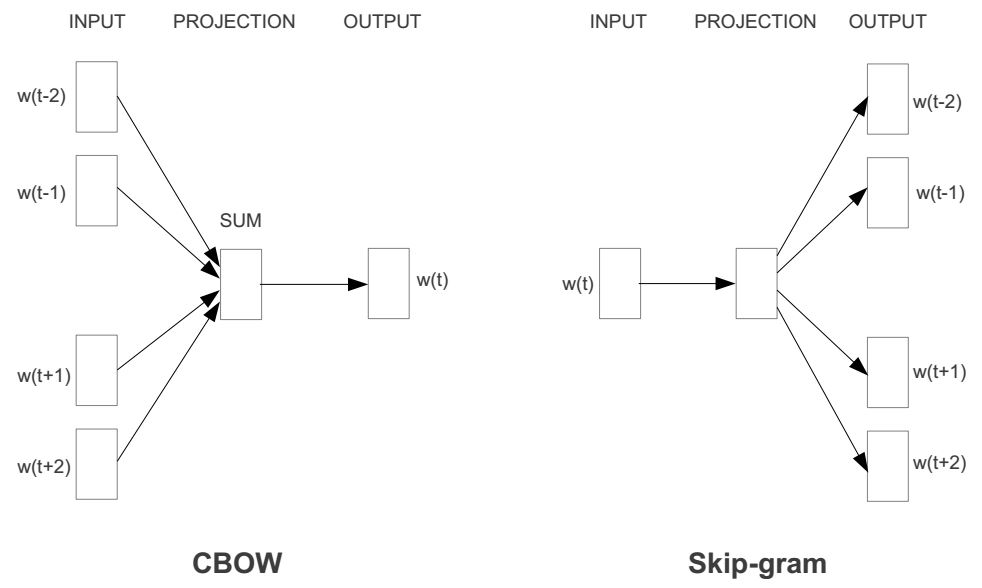
如何,这是不是镜像关系?所以接下来的讲解也会和skip-gram那篇文章极其类似。
前向传播
接下来我们来看下CBOW神经网络模型,CBOW的神经网络模型与skip-gram的神经网络模型也是互为镜像的
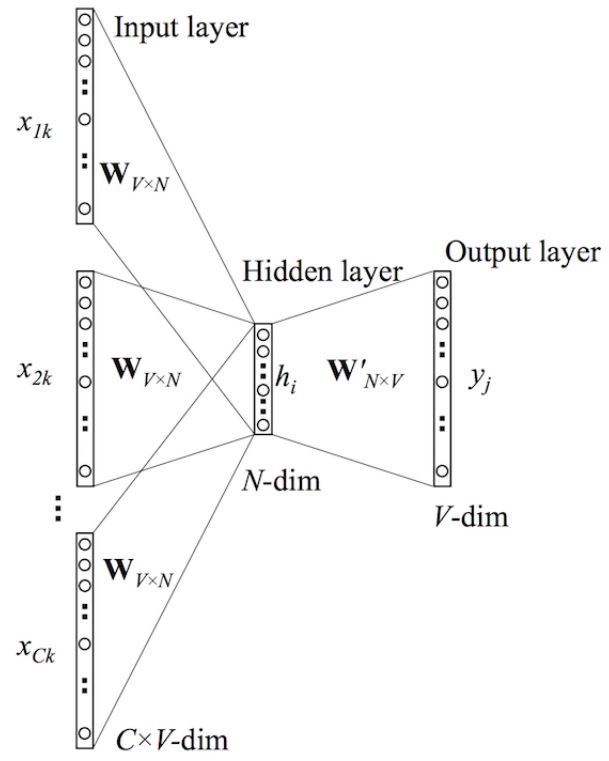
在上图中,该模型的输入输出与skip-gram模型的输入输出是相反的。这里输入层是由one-hot编码的输入上下文{
x
1
x_1
x1,…,
x
C
x_C
xC}组成,其中窗口大小为C,词汇表大小为V。隐藏层是N维的向量。最后输出层是也被one-hot编码的输出单词
y
y
y。被one-hot编码的输入向量通过一个
V
×
N
V\times N
V×N维的权重矩阵
W
W
W连接到隐藏层;隐藏层通过一个
N
×
V
N\times V
N×V的权重矩阵
W
′
W^{'}
W′连接到输出层。
接下来,我们假设我们知道输入与输出权重矩阵的大小。
- 第一步就是去计算隐藏层 h h h的输出。如下:
h = 1 C W ⋅ ( ∑ i = 1 C x i ) ( 1 ) h = \frac{1}{C}W\cdot (\sum_{i=1}^C x_i)\tag{$1$} h=C1W⋅(i=1∑Cxi)(1)
该输出就是输入向量的加权平均。这里的隐藏层与skip-gram的隐藏层明显不同。- 第二部就是计算在输出层每个结点的输入。如下:
u j = v w j ′ T ⋅ h ( 2 ) u_{j}=v^{'T}_{wj}\cdot h\tag{$2$} uj=vwj′T⋅h(2)
其中 v w j ′ T v^{'T}_{wj} vwj′T是输出矩阵 W ′ W^{'} W′的第 j j j列。- 最后我们计算输出层的输出,输出 y j y_j yj如下:
y c , j = p ( w y , j ∣ w 1 , . . . , w c ) = e x p ( u j ) ∑ j ′ = 1 V e x p ( u ′ j ) ( 3 ) y_{c,j} =p(w_{y,j}|w_1,...,w_c) = \frac{exp(u_{j})}{\sum^V_{j^{'}=1}exp(u^{'}j)}\tag{$3$} yc,j=p(wy,j∣w1,...,wc)=∑j′=1Vexp(u′j)exp(uj)(3)
通过BP(反向传播)算法及随机梯度下降来学习权重
在学习权重矩阵
W
W
W与
W
′
W^{'}
W′过程中,我们可以给这些权重赋一个随机值来初始化。然后按序训练样本,逐个观察输出与真实值之间的误差,并计算这些误差的梯度。并在梯度方向纠正权重矩阵。这种方法被称为随机梯度下降。但这个衍生出来的方法叫做反向传播误差算法。
具体推导步骤就不详写了:
- 首先就是定义损失函数,这个损失函数就是给定输入上下文的输出单词的条件概率,一般都是取对数,如下所示:
E = − l o g p ( w O ∣ w I ) ( 4 ) E = -logp(w_O|w_I)\tag{$4$} E=−logp(wO∣wI)(4)
= − v w o T ⋅ h − l o g ∑ j ′ = 1 V e x p ( v w T j ′ ⋅ h ) ( 5 ) = -v_{wo}^T\cdot h-log\sum_{j^{'}=1}^Vexp(v^T_w{_{j^{'}}}\cdot h)\tag{$5$} =−vwoT⋅h−logj′=1∑Vexp(vwTj′⋅h)(5)
接下来就是对上面的概率求导,具体推导过程可以去看BP算法,我们得到输出权重矩阵 W ′ W^{'} W′的更新规则:
w ′ ( n e w ) = w i j ′ ( o l d ) − η ⋅ ( y j − t j ) ⋅ h i ( 6 ) w^{'(new)} = w_{ij}^{'(old)}-\eta\cdot(y_{j}-t_{j})\cdot h_i\tag{$6$} w′(new)=wij′(old)−η⋅(yj−tj)⋅hi(6)
同理权重 W W W的更新规则如下:
w ( n e w ) = w i j ( o l d ) − η ⋅ 1 C ⋅ E H ( 7 ) w^{(new)} = w_{ij}^{(old)}-\eta\cdot\frac{1}{C}\cdot EH\tag{$7$} w(new)=wij(old)−η⋅C1⋅EH(7)
参考文献
[1] Mikolov T, Chen K, Corrado G, et al. Efficient Estimation of Word Representations in Vector Space[J]. Computer Science, 2013.(这篇文章就讲了两个模型:CBOW 和 Skip-gram)
[2] Mikolov T, Sutskever I, Chen K, et al. Distributed Representations of Words and Phrases and their Compositionality[J]. 2013, 26:3111-3119.(这篇文章针对Skip-gram模型计算复杂度高的问题提出了一些该进)
[3] Presentation on Word2Vec(这是NIPS 2013workshop上Mikolov的PPT报告)

























 467
467











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










