图的幂律度分布 power-law degree distributios

讲的一篇图论文中说到，“The natural graphs commonly found in the real-world have highly skewed power-law degree distributios ……”，开始只是了解个大概，后来经查才知道。power-law degree distributios原来是一种描述网络图中结点度的分布，中文可叫做“幂律度分布”。

维基百科词条“复杂网络”中对“无尺度网络”的介绍中，可对“幂律度分布”有进一步地了解。

资料解释如下：

网络的度分布，是指当随机地从网络中抽取一个节点时，与这个节点相连的节点数（叫做这个节点的度）d 的概率分布。
比如:对一个n个节点组成的完全图度分布是：d = n - 1 的概率是1，其余的都是0。
无尺度网络的度分布满足幂律分布，也就是说d = k 的概率正比于k 的某个幂次（一般是负的）：
\mathbb{P} (d = k) \propto k^{-\alpha}
（==加一句，这个符号是“正比于”的意思？？好吧~见过好几次了）
随机网络的度分布属于正态分布，因此有一个特征度数，即大部分节点的度数都接近它。
无尺度网络的度分布是呈集散分布：大部分的节点只有比较少的连接，而少数节点有大量的连接。由于不存在特征度数，因此得名“无尺度”。
无尺度网络的例子有很多。因特网、美国演员网络、细胞中蛋白质的交互网络都是无尺度网络。

无尺度网络的特性是：当节点意外失效或改变时，对网络的影响一般很小，只有很小的概率会发生大的影响，但当有集散节点受到影响时，网络受到的影响会比随机网络大得多。

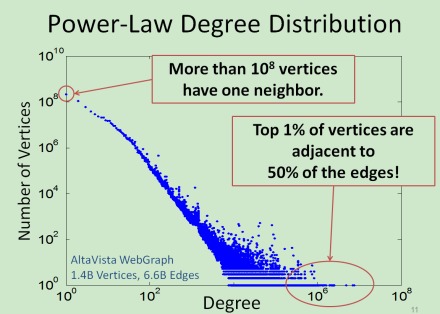
再盗个别人slides中的一个图。意思很明了，其中有1%的结点连接着一半的边，其余一半的边被剩余99%的结点所共用。