从稀疏表示到压缩感知（下）

原From <http://xiahouzuoxin.github.io/notes/html/%E7%99%BD%E8%AF%9D%E5%8E%8B%E7%BC%A9%E6%84%9F%E7%9F%A5.html>

python代码自己添加

   

1. 稀疏表示

使用压缩感知理论首先要求信号能表示为稀疏信号，如x=[1 0 0 0 1 0]，其中只有2个1，可认为是稀疏的。我们将信号通过一个矩阵映射到稀疏空间，

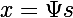
设信号x为N维，即

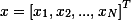
，则

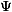
为NxN维稀疏表达矩阵，s即是将x进行稀疏表示后的Nx1维向量，其中大部分元素值为0。稀疏表示的原理就是通过线性空间映射，将信号在稀疏空间进行表示。

 

   

1.1傅里叶变换python下的演示

原型：

import numpy as np import matplotlib.pyplot as plt     # Compute the x and y coordinates for points on a sine curve #x = np.arange(0, 3 * np.pi, 0.1) #y = np.sin(x) t = np.arange(-300*np.pi,300*np.pi,0.1) x1=np.cos(2*np.pi*t/256)+np.sin(2*np.pi*t/128)     # Plot the points using matplotlib plt.plot(t, x1) plt.show() # You must call plt.show() to make graphics appear.

   

结果如图：

   

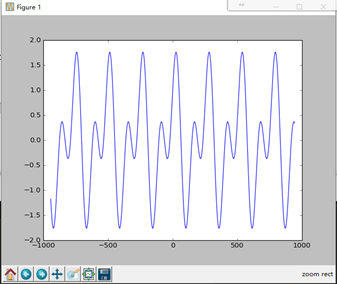
使用傅里叶对x1进行变换：