数据结构学习笔记（二）：二叉查找树

前一篇讲了数组及查找算法，本文则阐述一种新的数据结构：二叉查找树（Binary Search Tree，简写BST）。
其特点是：
1. 若左子树非空，则左子树上所有结点值均小于其根结点值;
2. 若右子树非空，则右子树上所有结点值均大于其根结点值;
3. 左、右子树也分别为二叉查找树
二叉查找树可提供快速的O(logN)级的插入、查找和删除。遍历的时间复杂度是O(N)级的。对于程序来说，不平衡的二叉搜索树要比平衡的二叉树简单得多，但有序数据能将它的性能降至O(N)级（操作始终在左子树或右子树上进行）。本文只阐述不平衡的二叉树，平衡二叉树下篇再讲。

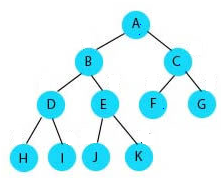
为方便后续代码示例的编写，这里先定义节点结构

/*BST节点结构，也是树结构系列文章的通用节点结构，后续不再重复声明*/
template<typename T>
class CTreeNode{
public:
    T          key;    /*键值*/
    CTreeNode* lchild; /*左子树*/
    CTreeNode* rchild; /*右字树*/
    CTreeNode* parent; /*父节点*/
    ...;
};

遍历

遍历的时间复杂度是O(N)。根据遍历的顺序分为前序、中序、后序三种。

前序遍历

遍历顺序：根节点–>左子树–>右子树

/*前序遍历算法，递归*/
template<typename T>
void PreOrder(CTreeNode<T>*& pRoot) const
{
    if(pRoot)
    {
        Print(pRoot->key); /*打印节点*/
        PreOrder(pRoot->lchild);
        PreOrder(pRoot->rchild);
    }
}
前图的前序遍历结果：A>B>D>H>I>E>J>K>C>F>G

中序遍历

遍历顺序：左子树–>根节点–>右子树

/*中序遍历算法，递归*/
template<typename T>
void InOrder(CTreeNode<T>*& pRoot) const
{
    if(pRoot)
    {       
        InOrder(pRoot->lchild);
        Print(pRoot->key); /*打印节点*/
        InOrder(pRoot->rchild);
    }
}
前图的中序遍历结果：H>D>I>B>J>E>K>A>F>C>G

后序遍历

遍历顺序：左子树–>右子树–>根节点

/*后序遍历算法，递归*/
template<typename T>
void PostOrder(CTreeNode<T>*& pRoot) const
{
    if(pRoot)
    {       
        PostOrder(pRoot->lchild);
        PostOrder(pRoot->rchild);
        Print(pRoot->key); /*打印节点*/ 
    }
}
前图的后序遍历结果：H>I>D>J>K>E>B>F>G>C>A

查找

查找的时间复杂度是O(logN)，但左子树或右子树缺失的情况下事二叉树会弱化成线性链表，时间复杂度为O(N)。有三种常用的查找场景：任意值、最小值、最大值。

任意值

/*查找任意值，递归实现*/
template<typename T>
CTreeNode<T>* Search(CTreeNode<T>* &pRoot, T key) const
{
    if(pRoot)
    {
        if(pRoot->key == key)
            return pRoot; /*当前节点*/
        if(key < pRoot->key)
            return Search(pRoot->lchild, key); /*左子树*/
        if(key > pRoot->key)
            return Search(pRoot->rchild, key); /*右子树*/
    }
    return NULL; /*没找到*/
}

最小值

/*查找最小的结点，当然是从左子树上入手了*/
template <typename T>
CTreeNode<T>* Minimum(CTreeNode<T>*&pRoot)
{
    CTreeNode<T>* tmp = pRoot;
    while(tmp ->lchild)
    {
        tmp = tmp->lchild;
    }
    return tmp;
}

最大值

/*查找最大的结点，当然是从右子树上入手了*/
template <typename T>
CTreeNode<T>* Maximum(CTreeNode<T>*&pRoot)
{
    CTreeNode<T>* tmp = pRoot;
    while(tmp ->rchild)
    {
        tmp = tmp->rchild;
    }
    return tmp;
}

插入

二叉树的插入即构建二叉树，遵循以下步骤：

1. 根结点为空则置为根节点
2. 值比根结点小，在左子树进行插入
3. 值比根结点大，在右子树进行插入

/*插入*/
template<typename T>
void Insert(CTreeNode<T>* &pRoot, CTreeNode<T>* pNew)
{
    CTreeNode<T>* parent= NULL;
    CTreeNode<T>* tmp = pRoot;
    /*寻找插入点*/
    while(tmp!=NULL)
    {
        parent = tmp;
        tmp= (pNew->key > tmp->key)? tmp->rchild : tmp->lchild;
    }

    pNew->parent = parent;
    if(parent == NULL) 
        pRoot = pNew; /*空树，新节点置为根节点*/
    else if(pNew->key > parent->key) /*右子树*/
        parent->rchild = pNew;
    else                          
        parent->lchild = pNew; /*左子树*/
}

删除

1. 叶子节点，直接删除
2. 只有一个子节点，让其父节点指向其子点即可
3. 有两个子子节点的删除策略：用其右子树最小节点代替该节点

/*删除节点, 例程中不包含节点数据的释放*/
template<typename T>
void Remove(CTreeNode<T>* &pRoot, T key)
{
    CTreeNode<T>* todo = Search(pRoot, key);
    if (todo) /*待删除的节点必须存在*/
    {
        if(todo->lchild == NULL && todo->rchild == NULL) 
        {
            /*删除叶子节点*/
            if (todo->parent->lchild == todo)
                todo->parent->lchild = NULL;
            else
                todo->parent->rchild = NULL;
        }
        else if(todo->lchild != NULL && todo->rchild == NULL)
        {
            /*只有左子树，左子树上移*/
            todo->parent->lchild = todo->lchild;
        }
        else if(todo->lchild == NULL && todo->rchild != NULL)
        {
            /*只有右子树，右子树上移*/
            todo->parent->rchild = todo->rchild;
        }
        else
        {
            /*左右子树都有，用其右子树最小节点代替该节点*/
            CTreeNode<T>* rmin = Minimum(todo->rchild);         
            if (todo->parent->lchild == todo)
                todo->parent->lchild = Clone(rmin);
            else
                todo->parent->rchild = Clone(rmin);
            Remove(rmin->parent, rmin->key);
        }
    }       
}

前驱和后继

前驱和后继指的是按某种顺序遍历时位于当前节点前面和后面的节点。

前序前驱

前序的遍历顺序：根–>左–>右
1. 前序根节点没有前驱
2. 前序左子树节点的前驱是父节点
3. 前序右子树节点的前驱是兄弟节点右子树的最大值，如果没有兄弟节点则前驱为父节点

template <typename T>
CTreeNode<T>* PreOrderPredecessor(CTreeNode<T>* pRoot, T key)
{
    if (pRoot == NULL)
        return NULL; /*空树*/

    /*确定key存在于树中*/
    CTreeNode<T>* pFound = Search(pRoot, key);
    if (pFound == NULL)
        return NULL; /*不存在*/

    /*前序根节点没有前驱*/
    if (pFound->parent == NULL)
        return NULL;

    /*前序左子树节点的前驱是父节点*/
    if (pFound->parent->lchild == pFound)
        return pFound->parent; 

    /*前序右子树节点的前驱是兄弟节点右子树的最大值*/
    CTreeNode<T>* pBrother = pFound->parent->lchild;
    if (pBrother == NULL) 
        return pFound->parent; /*没有兄弟节点则前驱为父节点*/
    return Maximum(pBrother->rchild);
}

前序后继

前序的遍历顺序：根–>左–>右
1. 某节点的后继是左子节点，
2. 某节点无左子树，则后继为右子节点
3. 某节点无左右子树，则后继为兄弟节点

template <typename T>
CTreeNode<T>* PreOrderSuccessor(CTreeNode<T>* pRoot, T key)
{
    if (pRoot == NULL)
        return NULL; /*空树*/

    /*确定key存在于树中*/
    CTreeNode<T>* pFound = Search(pRoot, key);
    if (pFound == NULL)
        return NULL; /*不存在*/

    /*某节点的后继是左子节点*/
    if (pFound->lchild)
        return pFound->lchild;

    /*某节点无左子树，则后继为右子节点*/
    if (pFound->rchild)
        return pFound->rchild;

    /*某节点无左右子树，则后继为兄弟节点*/
    if (pFound->parent == NULL)
        return NULL; /*已是最大值*/
    return pFound->parent->rchild; 
}

中序前驱

中序后继

后序前驱

后序后继