P问题、NP问题以及NP难问题的相关信息查找结果

在研究这方面问题之前，我先查询了一些基础知识，最终总结如下：
首先说明什么是时间复杂度，时间复杂度并不是表示一个程序解决问题需要花多少时间，而是当问题规模扩大后，程序需要的时间长度增长得有多快。
也就是说，对于高速处理数据的计算机来说，处理某一个特定数据的效率不能衡量一个程序的好坏，而应该看当这个数据的规模变大到数百倍后，程序运行时间是否还是一样，或者也跟着慢了数百倍，或者变慢了数万倍。
1.不管数据有多大，程序处理花的时间始终是那么多的，我们就说这个程序很好，具有O(1)的时间复杂度，也称常数级复杂度；
2.数据规模变得有多大，花的时间也跟着变得有多长，这个程序的时间复杂度就是O(n)，比如找n个数中的最大值；
3.而像冒泡排序、插入排序等，数据扩大2倍，时间变慢4倍的，属于O(n^2)的复杂度。
4.还有一些穷举类的算法，所需时间长度成几何阶数上涨，这就是O(a^n)的指数级复杂度，甚至O(n!)的阶乘级复杂度。
注：不会存在O(2*n^2)的复杂度，因为前面的那个“2”是系数，根本不会影响到整个程序的时间增长。同样地，O (n^3+n^2)的复杂度也就是O(n^3)的复杂度。因此，我们会说，一个O(0.01*n^3)的程序的效率比O(100*n^2)的效率低，尽管在n很小的时候，前者优于后者，但后者时间随数据规模增长得慢，最终O(n^3)的复杂度将远远超过O(n^2)。我们也说，O(n^100)的复杂度小于O(1.01^n)的复杂度。
容易看出，前面的几类复杂度被分为两种级别，其中后者的复杂度无论如何都远远大于前者：
1）O(1),O(log(n)),O(n^a) 等，我们把它叫做多项式级的复杂度，因为它的规模n出现在底数的位置；
2）O(a^n)和O(n!)型复杂度，它是非多项式级的，其复杂度计算机往往不能承受。
当我们在解决一个问题时，我们选择的算法通常都需要是多项式级的复杂度，非多项式级的复杂度需要的时间太多，往往会超时，除非是数据规模非常小。
自然地，人们会想到一个问题：
会不会所有的问题都可以找到复杂度为多项式级的算法呢？
答案是否定的。
有些问题甚至根本不可能找到一个正确的算法来，这称之为“不可解问题”(Undecidable Decision Problem)。
例如：Hamilton回路。
问题是这样的：给你一个图，问你能否找到一条经过每个顶点一次且恰好一次（不遗漏也不重复）最后又走回来的路（满足这个条件的路径叫做Hamilton回路）。
这个问题现在还没有找到多项式级的算法。事实上，这个问题就是我们后面要说的NPC问题。
定义：如果一个问题可以找到一个能在多项式的时间里解决它的算法，那么这个问题就属于P问题。
NP问题不是非P类问题。
NP问题是指可以在多项式的时间里验证一个解的问题。
NP问题的另一个定义是，可以在多项式的时间里猜出一个解的问题。
比方说，我人品很好，在程序中需要枚举时，我可以一猜一个准。
现在某人拿到了一个求最短路径的问题，问从起点到终点是否有一条小于100个单位长度的路线。它根据数据画好了图，但怎么也算不出来，于是来问我：你看怎么选条路走得最少？
我说，我人品很好，肯定能随便给你指条很短的路出来。然后我就胡乱画了几条线，说就这条吧。那人按我指的这条把权值加起来一看，嘿，神了，路径长度98，比100小。于是答案出来了，存在比100小的路径。
别人会问他这题怎么做出来的，他就可以说，因为我找到了一个比100 小的解。
在这个题中，找一个解很困难，但验证一个解很容易。验证一个解只需要O(n)的时间复杂度，也就是说我可以花O(n)的时间把我猜的路径的长度加出来。
那么，只要我人品好，猜得准，我一定能在多项式的时间里解决这个问题。我猜到的方案总是最优的，不满足题意的方案也不会来骗我去选它。这就是NP问题。
当然有不是NP问题的问题，即你猜到了解但是没用，因为你不能在多项式的时间里去验证它。
一个经典的例子，它指出了一个目前还没有办法在多项式的时间里验证一个解的问题。
很显然，前面所说的Hamilton回路是NP问题，因为验证一条路是否恰好经过了每一个顶点非常容易。但我要把问题换成这样：试问一个图中是否不存在Hamilton回路。这样问题就没法在多项式的时间里进行验证了，因为除非你试过所有的路，否则你不敢断定它“没有Hamilton回路”。
之所以要定义NP问题，是因为通常只有NP问题才可能找到多项式的算法。
我们不会指望一个连多项式地验证一个解都不行的问题存在一个解决它的多项式级的算法。
很显然，所有的P类问题都是NP问题。也就是说，能多项式地解决一个问题，必然能多项式地验证一个问题的解——既然正解都出来了，验证任意给定的解也只需要比较一下就可以了。
关键是，人们想知道，是否所有的NP问题都是P类问题。
目前为止这个问题还没有解决方法。但是，一个总的趋势、一个大方向是有的。人们普遍认为，P=NP不成立，也就是说，多数人相信，存在至少一个不可能有多项式级复杂度的算法的NP问题。
人们如此坚信P≠NP是有原因的，就是在研究NP问题的过程中找出了一类非常特殊的NP问题叫做NP-完全问题，也即所谓的NPC问题。C是英文单词“完全”的第一个字母。正是NPC问题的存在，使人们相信P≠NP。
NP完全问题(NP-C问题)，是世界七大数学难题之一。 NP的英文全称是Non-deterministic Polynomial的问题，即多项式复杂程度的非确定性问题。简单的写法是 NP=P？，问题就在这个问号上，到底是NP等于P，还是NP不等于P。
为了说明NPC问题，我们先引入一个概念——约化(Reducibility，有的资料上叫“归约”)
一个问题A可以约化为问题B的含义即是，可以用问题B的解法解决问题A，或者说，问题A可以“变成”问题B。
“问题A可约化为问题B”有一个重要的直观意义：B的时间复杂度高于或者等于A的时间复杂度。也就是说，问题A不比问题B难。这很容易理解。既然问题A能用问题B来解决，倘若B的时间复杂度比A的时间复杂度还低了，那A的算法就可以改进为B的算法，两者的时间复杂度还是相同。
约化具有一项重要的性质：约化具有传递性。如果问题A可约化为问题B，问题B可约化为问题C，则问题A一定可约化为问题C。
约化的标准概念：如果能找到这样一个变化法则，对任意一个程序A的输入，都能按这个法则变换成程序B的输入，使两程序的输出相同，那么我们说，问题A可约化为问题B。
我们所说的“可约化”是指的可“多项式地”约化(Polynomial-time Reducible)，即变换输入的方法是能在多项式的时间里完成的。约化的过程只有用多项式的时间完成才有意义。
NPC问题的定义非常简单。同时满足下面两个条件的问题就是NPC问题。
它得是一个NP问题；所有的NP问题都可以约化到它。
证明一个问题是 NPC问题也很简单。
先证明它至少是一个NP问题，再证明其中一个已知的NPC问题能约化到它（由约化的传递性，则NPC问题定义的第二条也得以满足。至于第一个NPC问题是怎么来的，下文将介绍），这样就可以说它是NPC问题了。
既然所有的NP问题都能约化成NPC问题，那么只要任意一个NPC问题找到了一个多项式的算法，那么所有的NP问题都能用这个算法解决了，NP也就等于P 了。
因此前文才说，“正是NPC问题的存在，使人们相信P≠NP”。我们可以就此直观地理解，NPC问题目前没有多项式的有效算法，只能用指数级甚至阶乘级复杂度的搜索。
NP-Hard问题是这样一种问题，它满足NPC问题定义的第二条但不一定要满足第一条，也就是NP-Hard问题要比NPC问题的范围广。
NPC问题是存在的。确实有这么一个非常具体的问题属于NPC问题——-逻辑电路问题是NPC类问题的“鼻祖”。是第一个NPC问题。其它的NPC问题都是由这个问题约化而来的。
逻辑电路问题是指的这样一个问题：给定一个逻辑电路，问是否存在一种输入使输出为True。
逻辑电路问题属于NPC问题。这是有严格证明的。证明过程相当复杂，其大概意思是说任意一个NP问题的输入和输出都可以转换成逻辑电路的输入和输出（想想计算机内部也不过是一些0和1的运算），因此对于一个NP问题来说，问题转化为了求出满足结果为True的一个输入（即一个可行解）。
有了第一个NPC 问题后，一大堆NPC问题就出现了，因为再证明一个新的NPC问题只需要将一个已知的NPC问题约化到它就行了。后来，Hamilton 回路成了NPC问题，TSP问题也成了NPC问题。
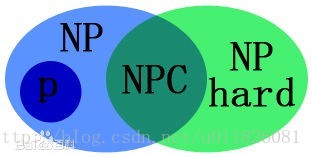
以下为范围示意图：