1、排序
对数组进行排序,然后前K个元素就是需要查找的元素,排序的方法可以采用快速排序,但是我们知道在快速排序中如果已经是有序的数组,采用快速排序的时间复杂度是O(N^2),为了解决这种问题,通常选择随机选择一个数组值pivot作为基准,将数组分为S1 =< pivot和S2 > pivot,这样就能避免快速排序中存在的问题,或者采用随机选择三个元素,然后取中间值作为基准就能避免快速算法的最差时间复杂度,这种方法的前K个数字是有序的。
2、利用快排中的pivot特性
既然是选择前K个对象,那么就没必要对所有的对象进行排序,可以采用快速选择的思想获得前K个对象,比如首先采用快速排序的集合划分方法划分集合:S1,pivot,S2,然后比较K是否小于S1的个数,如何小于,则直接对S1进行快速排序,如果K的个数超过S1,那么对S2进行快速排序,排序完成之后,取数组的前K个元素就是数组的前K个最小值。这种实现方法肯定比第一种的全快速排序要更快速。
3、将数组转换为最小堆的情况
根据最小堆的特性,第一个元素肯定就是数组中的最小值,这时候我们可以将元素保存起来,然后将最后一个元素提升到第一个元素,重新构建最小堆,这样进行K次的最小堆创建,就找到了前K个最小值,这是运用了最小堆的特性,实质上是最小堆的删除实现方法。这种算法的好处是实现了数组的原地排序,并不需要额外的内存空间。
4、接下来的这种思想有点类似桶排序
首先给定一个K个大小的数组b,然后复制数组a中的前K个数到数组b中,将这K个数当成数组a的前K个最小值,对数组b创建最大堆,这时候再次比较数组a中的其他元素,如果其他元素小于数组b的最大值(堆顶),则将堆顶的值进行替换,并重新创建最大堆。这样遍历一次数组就找到了前K个最小元素。这种方法运用了额外的内存空间,特别当选择的K值比较大时,这种方法有待于权衡一下。 这种方法对于海量数据来说是有较好的作用,对于海量数据不能全部存放在内存中,这时候创建一个较小的
数组空间,然后创建最大堆,从硬盘中读取其他的数据,进而实现前K个数据的查找。
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<assert.h>
#include<time.h>
#define LEN 500000
#define K 100
/*堆的性质*/
#define LEFTSON(i) (2*(i)+1)
#define RIGHTSON(i) (2*((i)+1))
#define PARENT(i) (((i)-1)/2)
void swap(int *a, int *b)
{
assert(a != NULL && b != NULL);
if(a != b)
{
*a = *a ^ *b;
*b = *a ^ *b;
*a = *a ^ *b;
}
}
int partition(int *a, int left, int right)
{
int pivot = a[right];
int i = left;
int j = left - 1;
assert(a != NULL);
for(i = left; i < right; ++ i)
{
if(a[i] < pivot)
{
++ j;
swap(&a[i],&a[j]);
}
}
swap(&a[j + 1],&a[right]);
return (j + 1);
}
void quicksort(int *a, int left, int right)
{
int i = 0;
assert(a != NULL);
if(left < right)
{
i = partition(a,left,right);
quicksort(a, left, i - 1);
quicksort(a, i + 1, right);
}
}
int QuickSort(int *a, int size)
{
assert(a != NULL);
quicksort(a,0,size-1);
}
void quickselect(int *a, int left, int right, int k)
{
int i = 0;
assert(a != NULL && left <= k
&& left <= right && k <= right);
if(left < right)
{
i = partition(a, left, right);
if(i + 1 <= k)
quickselect(a, i + 1 , right, k);
else if(i > k)
quickselect(a, left, i - 1, k);
}
}
void QuickSelect(int *a, int size, int k)
{
assert(a != NULL);
quickselect(a, 0, size - 1, k);
}
/*最大堆*/
void max_heapify(int *a, int left, int right)
{
int tmp = 0;
int child = left;
int parent = left;
assert(a != NULL);
for(tmp = a[parent]; LEFTSON(parent) <= right;parent = child)
{
child = LEFTSON(parent);
if(child != right && a[child] < a[child + 1])
child ++;
if(tmp < a[child])
a[parent] = a[child];
else /*满足最大堆的特性,直接退出*/
break;
}
a[parent] = tmp;
}
/*创建最大堆*/
void build_maxheap(int *a, int size)
{
int i = 0;
assert(a != NULL);
for(i = PARENT(size); i >= 0 ; -- i)
max_heapify(a,i,size - 1);
}
/*最小堆的实现*/
void min_heapify(int *a, int left, int right)
{
int child = 0;
int tmp = 0;
int parent = left;
assert(a != NULL);
for(tmp = a[parent]; LEFTSON(parent) <= right; parent = child)
{
child = LEFTSON(parent);
if(child != parent && a[child] > a[child + 1])
child ++;
if(a[child] < tmp)
a[parent] = a[child];
else /*满足最小堆的特性,直接退出*/
break;
}
a[parent] = tmp;
}
/*创建最小堆*/
void build_minheap(int *a, int size)
{
int i = PARENT(size);
assert(a != NULL);
for(; i >= 0; -- i)
min_heapify(a, i, size - 1);
}
/*采用快速排序查找*/
void find_Kmin_num_1(int *a , int size, int k)
{
int i = 0;
assert(a != NULL);
QuickSort(a, size);
#if 0
for(i = 0; i < k ; ++ i)
printf("%d\t",a[i]);
printf("\n");
#endif
}
/*采用快速选择实现*/
void find_Kmin_num_2(int *a, int size, int k)
{
int i = 0;
assert(a != NULL);
QuickSelect(a, size, k);
#if 0
for(i = 0; i < k ; ++ i)
printf("%d\t",a[i]);
printf("\n");
#endif
}
/*采用最大堆实现*/
void find_Kmin_num_3(int *a, int size, int k)
{
int i = 0;
int *b =(int *) malloc(sizeof(int)*k);
assert(a != NULL && b != NULL);
for(i = 0; i < k; ++ i)
b[i] = a[i];
build_maxheap(b,k);
for(; i < size; ++ i)
{
if(a[i] < b[0])
{
b[0] = a[i];
// build_maxheap(b , k);
max_heapify(b,0,k - 1);
}
}
#if 0
for(i = 0; i < k ; ++ i)
printf("%d\t",b[i]);
printf("\n");
#endif
}
/*采用最小堆删除元素的方式实现*/
void find_Kmin_num_4(int *a ,int size, int k)
{
int i = 0;
assert(a != NULL);
build_minheap(a, size - 1);
for(i = 0; i < k; ++ i)
{
// printf("%d\t",a[0]);
/*删除a[0],释放a[size - 1 - i]*/
a[0] = a[size -1 - i];
min_heapify(a, 0, size - 2 - i);
}
// printf("\n");
}
int main()
{
int a[LEN];
int b[LEN];
int c[LEN];
int d[LEN];
int i = 0,j = 0;
clock_t _start;
double times = 0;
srand((int)time(NULL));
for(i = 0; i < LEN; ++ i)
{
a[i] = rand()%(LEN);
b[i] = a[i];
c[i] = a[i];
d[i] = a[i];
// printf("%d\t",a[i]);
}
// printf("\n");
_start = clock();
find_Kmin_num_1(a,LEN,K);
times = (double)(clock() - _start)/CLOCKS_PER_SEC;
printf("快速排序的查找需要:%f\n",times);
_start = clock();
find_Kmin_num_2(b,LEN,K);
times = (double)(clock() - _start)/CLOCKS_PER_SEC;
printf("快速选择的查找需要:%f\n",times);
_start = clock();
find_Kmin_num_3(c,LEN,K);
times = (double)(clock() - _start)/CLOCKS_PER_SEC;
printf("最大堆的查找需要:%f\n",times);
_start = clock();
find_Kmin_num_4(d,LEN,K);
times = (double)(clock() - _start)/CLOCKS_PER_SEC;
printf("最小堆的查找需要:%f\n",times);
return 0;
}
5、SELECT算法,它能在时间复杂度为O(N)的情况下找出第K大的数
第一步:把数组分成n/5这么多子数组,每个子数组里包含5个数,因为会有无法整出的可能,所以最后一个子数组会小于5.
第二步:用insertionsorting把这5个数排序,然后找出中位数,也就是第3个。
第三步:把获得的中位数又排序,找出中位数的中位数。如果中位数的个数是偶数,那么取排好序的第m/2个数,m指的是中位数的个数。
第四步:然后呢,把原来的数组分成两个部分,一部分比那个“中位数的中位数”大,一部分比那个“中位数的中位数”小。我们可以假设左边的数大,右边的数小。然后我们可以得到“中位数的中位数”的位置i.
第五步:如果i = k,那么那个“中位数的中位数”就是第k大的数。如果 i < k,不用说,第k大的在“中位数的中位数”的右边,否则就在左边。我们一直recursely这么做,那么就一定能够找到第K大的值了。
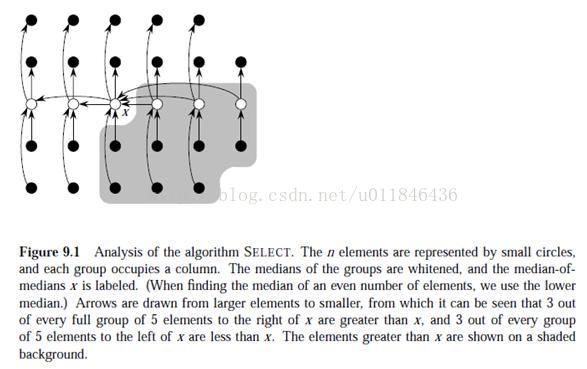
其实,算法还是比较容易懂得,关键的关键,是复杂度的分析。如果能够知道复杂度如何求出来的,那么,对算法本身就了解得更清楚。要讲复杂度,首先看一个图。
图中的X 就是“中位数的中位数”, 而且箭头的方向是从大数指到小数。所以,我们可以知道,至少灰色区域的都比X大,这是整个复杂度分析的关键,而,其它点能否说它比X大,我们不能保证。而灰色区域里最多有多少个数呢?因为X是中位数的中位数,所以,比X大的中位数最少有 [(n/5l)* (1/2) - 2] 个(这个值也是关键),这里减2是因为要去除X本身,第二呢,还要去除一个中位数---这个中位数所在的子数组个数小于5. 所以,最坏最坏的情况,第K大的值不在灰色区域里,那么我们就要对剩下部分进行不断的SELECT。剩余部分就是n -3 [(\lfloor n/5 \rfool) * (1/2) - 2] = O(7n/10) .
整个过程中,第1,2,4步所需时间为O(n), 注意第2步的复杂度不为O(n^2),第3步的复杂度为 T(n/5),第五步的复杂度为 T(7n/10)。
所以,复杂度的递归公式为: T(n)= T(n/5) + T(7n/10) + O(n), 算出来以后T(n) =O(n).
























 840
840











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








