3401 - Colored Cubes

Colored Cubes

Time limit: 3.000 seconds

There are several colored cubes. All of them are of the same size but they may be colored differently. Each

face of these cubes has a single color. Colors of distinct faces of a cube may or may not be the same.

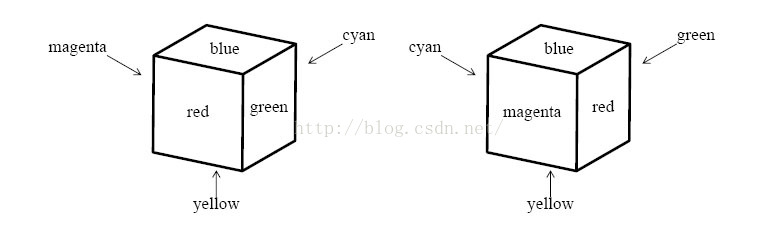
Two cubes are said to beidentically colored if some suitable rotations of one of the cubes give identical

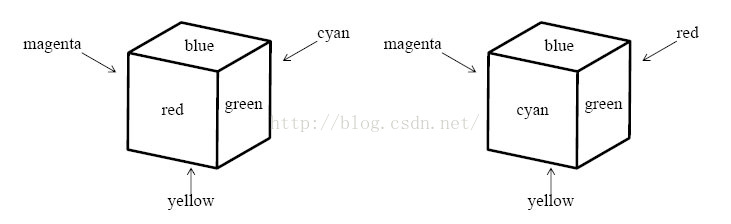
looks to both of the cubes. For example, two cubes shown in Figure 2 are identically colored. A set of cubes is said to be identically colored if every pair of them are identically colored.

A cube and its mirror image are not necessarily identically colored. For example, two cubes shown in Figure 3

are not identically colored.

You can make a given set of cubes identically colored by repainting some of the faces, whatever colors the

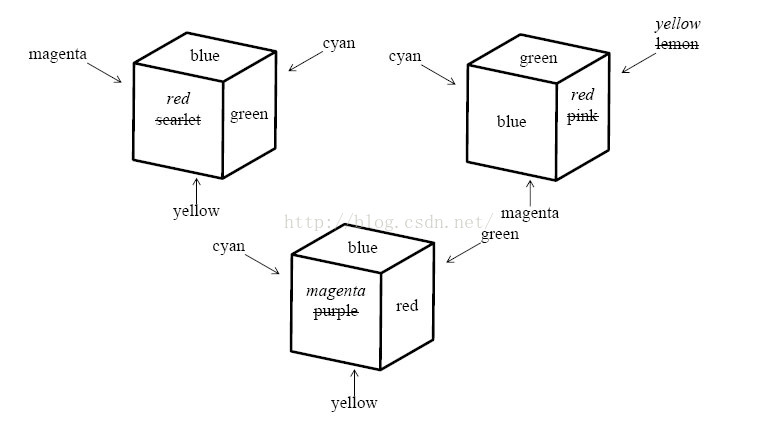
faces may have. In Figure 4, repainting four faces makes the three cubes identically colored and repainting fewer faces will never do.

Your task is to write a program to calculate the minimum number of faces that needs to be repainted for a

given set of cubes to become identically colored.

Input：

The input is a sequence of datasets. A dataset consists of a header and a body appearing in this order. A

header is a line containing one positive integernand the body following it consists of n lines. You can assume that1n4 . Each line in a body contains six color names separated by a space. A color name consists of a word or words connected with a hyphen (-). A word consists of one or more lowercase letters. You can assume that a color name is at most 24-characters long including hyphens.

A dataset corresponds to a set of colored cubes. The integern corresponds to the number of cubes. Each line

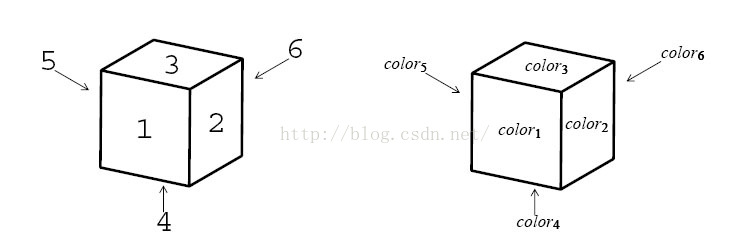
of the body corresponds to a cube and describes the colors of its faces. Color names in a line is ordered in accordance with the numbering of faces shown in Figure 5. A line color₁color₂color₃color₄color₅color₆

corresponds to a cube colored as shown in Figure 6.

The end of the input is indicated by a line containing a single zero. It is not a dataset nor a part of a

dataset. 

Figure 2: Identically colored cubes

Figure 3: cubes that are not identically colored

Figure 4: An example of recoloring 

Figure 5: Numbering of faces Figure 6: Coloring

Output：

For each dataset, output a line containing the minimum number of faces that need to be repainted to make the

set of cub es identically colored. 

Sample Input：

3 
scarlet green blue yellow magenta cyan 
blue pink green magenta cyan lemon 
purple red blue yellow cyan green 
2 
red green blue yellow magenta cyan 
cyan green blue yellow magenta red 
2 
red green gray gray magenta cyan 
cyan green gray gray magenta red 
2 
red green blue yellow magenta cyan 
magenta red blue yellow cyan green 
3 
red green blue yellow magenta cyan 
cyan green blue yellow magenta red 
magenta red blue yellow cyan green 
3 
blue green green green green blue 
green blue blue green green green 
green green green green green sea-green 
3 
red yellow red yellow red yellow 
red red yellow yellow red yellow 
red red red red red red 
4 
violet violet salmon salmon salmon salmon 
violet salmon salmon salmon salmon violet 
violet violet salmon salmon violet violet 
violet violet violet violet salmon salmon 
1 
red green blue yellow magenta cyan 
4 
magenta pink red scarlet vermilion wine-red 
aquamarine blue cyan indigo sky-blue turquoise-blue 
blond cream chrome-yellow lemon olive yellow 
chrome-green emerald-green green olive vilidian sky-blue 
0

Sample Output：
4 
2 
0 
0 
2 
3 
4 
4 
0 
16

    题目意思是有n个带颜色的立方体，立方体的每个面都涂有一种颜色。要求重新涂尽量少的颜色使得所有立方体完全相同。也就是说将一个立方体旋转后，使得立方体对 应面的颜色相同。由于给你的立方体最多只有4个，暴力枚举的方法可行。枚举则可以通过枚举每个正方体的姿态（将标准姿态定为正面为1、右面为2、顶面为3、底面为4、左面为5、右面为6）即通过旋转来改变姿态，然后对于6个面，选出一个出现次数最多的颜色作为“标准”，将和其颜色不相同的进行重新涂色。当选择一个面朝上时，朝正面的情况有4种，因此每个立方体拥有24种姿态。（立方体的各面顺序：正，右，底，左，后）

当1朝向正面时，立方体的其他面的情况为：{0,2,4,1,3,5}, {0,1,2,3,4,5}, {0,3,1,4,2,5}, {0,4,3,2,1,5}；

当2朝向正面时，立方体的其他面的情况为：{1,2,0,5,3,4}, {1,5,2,3,0,4}, {1,3,5,0,2,4}, {1,0,3,2,5,4}；
当4朝向正面时，立方体的其他面的情况为：{2,1,5,0,4,3}, {2,0,1,4,5,3}, {2,4,0,5,1,3}, {2,5,4,1,0,3}；
当4朝向正面时，立方体的其他面的情况为：{3,4,5,0,1,2}, {3,5,1,4,0,2}, {3,1,0,5,4,2}, {3,0,4,1,5,2}；
当5朝向正面时，立方体的其他面的情况为：{4,0,2,3,5,1}, {4,2,5,0,3,1}, {4,5,3,2,0,1}, {4,3,0,5,2,1}；
当6朝向正面时，立方体的其他面的情况为：{5,2,1,4,3,0}, {5,4,2,3,1,0}, {5,1,3,2,4,0}, {5,3,4,1,2,0}；
然后将读入的颜色不变，将面的正面朝向情况取匹配颜色（第一组数据：1朝上时，scarlet面为1，二朝上时，scarlet面为2；）

#include <stdio.h>
#include <math.h>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;

#define fors(i,n) for(int i = 0; i < n; ++i)///将for循环进行宏定义，减少for语句的出现使得代码更加简洁
char maps[4][6][50];///用来存储每个立方体的6个面的颜色数据
int cases[24][6] = {
{1,2,0,5,3,4}, {1,5,2,3,0,4}, {1,3,5,0,2,4}, {1,0,3,2,5,4},
{2,1,5,0,4,3}, {2,0,1,4,5,3}, {2,4,0,5,1,3}, {2,5,4,1,0,3},
{3,4,5,0,1,2}, {3,5,1,4,0,2}, {3,1,0,5,4,2}, {3,0,4,1,5,2},
{4,0,2,3,5,1}, {4,2,5,0,3,1}, {4,5,3,2,0,1}, {4,3,0,5,2,1},
{5,2,1,4,3,0}, {5,4,2,3,1,0}, {5,1,3,2,4,0}, {5,3,4,1,2,0},
{0,2,4,1,3,5}, {0,1,2,3,4,5}, {0,3,1,4,2,5}, {0,4,3,2,1,5}
};///枚举出一个立方体的24种姿态

const int MAX = 1000000;
int Min = MAX, n, data[4];

int color(char ch[5][50])///判断ch的4个面需要涂色的个数
{
    int counts[5] = {0};
    fors(i,n) fors(j,n) ///对两个立方体进行旋转并统计颜色相同的面的数目
        if(!strcmp(ch[i],ch[j]))
            counts[i]++;
    int Max = 0;
    fors(c,n)
        if(counts[c] > counts[Max])///找出一个面使得其与另外一个正方体颜色相同的面的数目最多
            Max = c;
    int flag = 0;
    fors(i,n)
        if(strcmp(ch[i],ch[Max]))///与出现次数最多的颜色进行比较，不同则对重新涂色
            flag++;
    return flag;
}

void mem()///统计所需涂色的最少次数
{
    int sum  = 0;
    fors(i,6)
    {
        char bj[5][50];
        fors(j,n)///将正方体的24种姿态与给出的颜色进行匹配
            strcpy(bj[j],maps[j][cases[data[j]][i]]);
        sum += color(bj);///统计出需要涂色的数目
    }
    if(sum < Min)
        Min = sum;
}

void dfs(int deep)
{
    if(deep == n - 1)
        mem();
    else
    {
        fors(i,24)
        {
            data[deep] = i;
            dfs(deep+1);
        }
    }
}

int main()
{
    while(scanf("%d",&n)&&n!=0)
    {
        fors(i,n) fors(j,6)
            scanf("%s",maps[i][j]);
        Min= MAX;
        dfs(0);
        printf("%d\n",Min);
    }
    return 0;
}