xmu 1016 Magic Square

Description

    In recreational mathematics, a magic square of order n is an arrangement of n² numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n². The term "magic square" is also sometimes used to refer to any of various types of word square.

    Normal magic squares exist for all orders n ≥ 1 except n = 2, although the case n = 1 is trivial—it consists of a single cell containing the number 1. The smallest nontrivial case, shown below, is of order 3.(Lo Shu Square)

    The constant sum in every row, column and diagonal is called the magic constant or magic sum, M. The magic constant of a normal magic square depends only on n and has the value

    For normal magic squares of order n = 3, 4, 5, …, the magic constants are: 15, 34, 65, 111, 175, 260, …

--From Wikipedia, the free encyclopedia

    TheBeet is fond of Magic Square. He can make up a Magic Square as a piece of cake if n is small. But when n becomes larger, he gives up. Can you help the poor guy?

Input

Each input file contains only one integer N (3 <= N <= 500).

 

Output

Output an N*N matrix. Each element should range in [1..N*N]. If there are multiple solutions,any of them will getAccepted.

 

Sample Input

3

Sample Output

2 7 6

9 5 1

4 3 8

 

Hint

This is a SPJ.

Source

xmu

 

题目就是让你构造一个N阶的幻方。简单说下幻方的构造

1 奇数阶幻方构造法

(1) 将1放在第一行中间一列;

(2) 从2开始直到n×n止各数依次按下列规则存放：向右上方向摆放

(3) 如果行或者列中只有一个超出了范围即大于n或者小于1

(4) 如果按上面规则确定的位置上已有数，或上一个数是第1行第n列时，则把下一个数放在上一个数的下面。

 

 

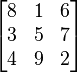2 双偶数阶幻方构造

 4m阶的幻方

(1) 把数1到n×n按从上至下，从左到右顺序填入矩阵

(2) 平均分成4部分将左上角坐标相加为偶数和左下角坐标相加为奇数的点分别于右下角和右上角交换，具体参考代码就更懂了

3 单偶数阶幻方构造

 4m+2阶幻方构造

(1)把这个4m+2的幻方平均分成4部分记为A,B,C,D 对应位置如下

   A C

   D B

将1到(4m+2)^2 这些数由小到大平均分成4部分，分配给ABCD按照上面的奇数构造法则构造4个(2m+1)阶的幻方

(2)选中A中部分数字，包括：m+1行从左向右前（m-1）个数字，其他行前m个数字。与D中对应的数字交换

(3)选中C中部分数字，包括：每一行从右向左前（M-1）个数字。与B中对应的部分交换

构造完毕

 

下面是对应实现的代码

#include<stdio.h>
#define N 500
int a[N][N],n,line,row,sp,i,j;
void ji(int an)
{
	int hehe=an*an;
	row=an>>1;
	line=0;	
	for(i=0;i<an;i++)
		for(j=0;j<an;j++)
			a[i][j]=0;
		a[line][row]=1;
		for(i=2;i<=hehe;i++)
		{
			if(a[(line-1+an)%an][(row+1)%an]==0)
			{
				line=(line-1+an)%an;
				row=(row+1)%an;
				a[line][row]=i;
			}
			else
			{
				line=(line+1)%an;
				a[line][row]=i;
			}
		}
}
void si()
{
	int temp=1,m,flag,nn;
	for(i=0;i<n;i++)
		for(j=0;j<n;j++)
		{
			a[i][j]=temp;
			temp++;
		}
		m=n>>1;
		nn=n-1;
		for(i=0;i<m;i++)
		{
			for(j=0;j<m;j++)
			{
				if(((i+j)&1)==0)
				{
					temp=a[nn-i][nn-j];
					a[nn-i][nn-j]=a[i][j];
					a[i][j]=temp;
				}
			}
		}
		for(i=m;i<n;i++)
		{
			for(j=0;j<m;j++)
			{
				if((i+j)&1)
				{
					temp=a[nn-i][nn-j];
					a[nn-i][nn-j]=a[i][j];
					a[i][j]=temp;
				
				}		
			}
		}
}		
void sijia()
{
	int temp;
	int k=(n-2)/4,b,c,d;
	int s=k+k+1;
	ji(s);
	b=s*s;
	c=b+b;
	d=b+c;
	for(i=0;i<s;i++)
		for(j=s;j<n;j++)
			a[i][j]=a[i][j-s]+c;
	for(i=s;i<n;i++)
		for(j=0;j<s;j++)
			a[i][j]=a[i-s][j]+d;
	for(i=s;i<n;i++)
		for(j=s;j<n;j++)
			a[i][j]=a[i-s][j-s]+b;
	for(i=0;i<s;i++)
		for(j=0;j<k;j++)
		{
			temp=a[i+s][j];
			a[i+s][j]=a[i][j];
			a[i][j]=temp;
		}
	temp=a[k+s][k];
	a[k+s][j]=a[k][k];
	a[k][k]=temp;
	temp=a[k+s][0];
	a[k+s][0]=a[k][0];
	a[k][0]=temp;
	for(i=0;i<s;i++)
		for(j=n-k+1;j<n;j++)
		{
			temp=a[i+s][j];
			a[i+s][j]=a[i][j];
			a[i][j]=temp;
		}

}
int main()
{
	scanf("%d",&n);
	if(n&1)
		ji(n);
	else if (n%4==0)
		si();
	else
		sijia();
	for(i=0;i<n;i++)
	{
		for(j=0;j<n-1;j++)
		{
			printf("%d ",a[i][j]);
		}
		printf("%d\n",a[i][j]);
	}	
	
	return 0;
}

至于为什么这么构造可以我有空再补上