算法导论第十一(11)章散列(Hash)表知识点梳理及详细课后答案

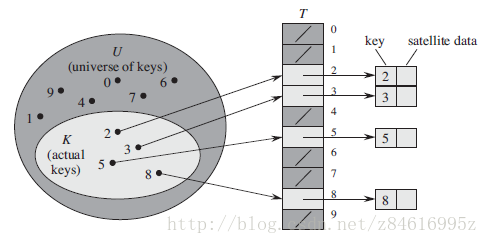
11.1直接寻址表

关键字集合U = { 0, 1, ..., m - 1 }，实际的关键字集合K。

用一个数组T[0..m - 1]，其中每个位置对应U中的一个关键字k。

把关键字k映射到槽T(k)上的过程称为散列。

散表表仅支持INSERT、SEARCH、DELETE操作。

11.1-1假设一动态集合S用一个长度为m的直接寻址表T表示。请给出一个查找S中最大元素的过程。你所给的过程在最坏情况下的运行时间是多少？

查找指定元素所用时间为O(1),如果找表中最大值，那么最坏情况下需要循环遍历散列表中所有有效值以确定最大值。运行时间为O(m).

[cpp]  view plain  copy

1. struct Hash* direct_address_search(struct Hash *T[], int key)  
2. {  
3.     int Max=0;  
4.     while (key!=MAX)//MAX表示散列表容量最大值  
5.     {  
6.         if (T[key]!=NULL&&Max<T[key]->key)  
7.         {  
8.              Max=T[key]->key;          
9.         }  
10.         key++;//key既可以表示直接寻址表T的下标，也可以表示关键字  
11.     }  
12. }  

11.1-2位向量是一个仅包含0和1的数组。长度为m的位向量所占空间要比包含m个指针的数组少得多，请说明如何用一个位向量表示一个包含不同元素(无卫星数据)的动态集合。字典操作的运行时间应为O(1).

核心思想：如果插入元素x,那么把位向量的第x位设置为1，否则为0.  如果删除元素x,那么把位向量的第x位设置为0。

[cpp]  view plain  copy

1. #include <stdio.h>    
2. #include <stdlib.h>   
3. #define INT_BIT 32    
4. typedef struct {    
5.     unsigned int *table;    
6.     int size;    
7. } BitMap;    
8.   
9. BitMap * bitmap_create(int max)    
10. {    
11.     BitMap *bitmap = (BitMap *)malloc(sizeof(BitMap));    
12.     bitmap->size = max / INT_BIT + 1;   
13.     bitmap->table =(unsigned int *) calloc(sizeof(int), bitmap->size);    
14.     return bitmap;    
15. }    
16.   
17. void bitmap_insert(BitMap *bitmap, int key)    
18. {    
19.     bitmap->table[key / INT_BIT] = bitmap->table[key / INT_BIT] |(1 << (key % INT_BIT));    
20. }    
21.   
22. void bitmap_delete(BitMap *bitmap, int key)    
23. {    
24.     bitmap->table[key / INT_BIT] &= ~(1 << (key % INT_BIT));    
25. }    
26.   
27. int bitmap_search(BitMap *bitmap, int key)    
28. {    
29.     return bitmap->table[key / INT_BIT] & (1 << (key % INT_BIT));    
30. }    
31.   
32. void bitmap_print(BitMap *bitmap)    
33. {    
34.     printf("-----\n");    
35.     int i;    
36.     for (i = 0; i < bitmap->size; i++)    
37.         if (bitmap->table[i] != 0)    
38.             printf("%d: %d\n ", i, bitmap->table[i]);    
39.         printf("-----\n");    
40. }    
41.   
42. int main(void)    
43. {    
44.     BitMap *bitmap = bitmap_create(1024);    
45.     bitmap_insert(bitmap, 15);    
46.     bitmap_insert(bitmap, 10);  
47.     bitmap_insert(bitmap, 520);    
48.     bitmap_insert(bitmap, 900);  
49.     bitmap_delete(bitmap, 10);  
50.     bitmap_print(bitmap);     
51.     printf("%d\n", bitmap_search(bitmap, 68));    
52.     printf("%d\n", bitmap_search(bitmap, 520));    
53.     return 1;    
54. }  

参考资料来自：
直接寻址表的位向量表示

11.1-3试说明如何实现一个直接寻址表，表中各元素的关键字不必都不相同，且各元素可以有卫星数据。所有三种字典操作(INSERT,DELETE和SEARCH)的运行时间应为O(1)

(不要忘记DELETE要处理的是被删除对象的指针变量，而不是关键字)。

[cpp]  view plain  copy

1. #include <stdio.h>  
2. #include <stdlib.h>  
3. #define LEN sizeof(struct Hash)  
4. #define MAX 6  
5.    
6.   struct Hash{  
7.      int key;  
8.      int satellite;  
9.  }Data;                               //元素结构体，有关键字和卫星数据  
10.    
11.  struct Hash* direct_address_search(struct Hash *T[], int key);        //散列表查找操作  
12.    
13.  void direct_address_insert(struct Hash *T[], struct Hash *x);         //散列表插入操作  
14.    
15.  void direct_address_delete(struct Hash *T[], struct Hash *x);         //散列表删除操作  
16.    
17.  void print_table(struct Hash *T[]);                            //打印散列表（为了方便查看删除操作后，散列表的变化）  
18.    
19.  int main(){  
20.      int i, key, satellite;  
21.      struct Hash *data[MAX];  
22.      struct Hash *d;  
23.      for(i = 0; i < MAX; i++){  
24.          data[i] =new struct Hash [LEN];  
25.          data[i] = NULL;  
26.      }  
27.        
28.      for(i = 0; i <= 3; i++){  
29.          d = new struct Hash[LEN];  
30.         printf("Input the key_value:\n");  
31.          scanf("%d", &key);  
32.          printf("Input the satellite:\n");  
33.          scanf("%d", &satellite);  
34.          d->key = key;  
35.          d->satellite = satellite;  
36.          direct_address_insert(data, d);  
37.      }  
38.      print_table(data);  
39.      printf("请输入待查找的元素\n");  
40.      scanf("%d", &key);  
41.      d = direct_address_search(data, key);  
42.      if (d)  
43.      {  
44.          printf("the key is %d, and its satellite is %d\n", d->key, d->satellite);  
45.      }   
46.      else  
47.      {  
48.          printf("没有找到\n");  
49.      }  
50.      if (d)  
51.      {  
52.          direct_address_delete(data, d);  
53.      }  
54.       print_table(data);  
55.      delete d;  
56.     for(i = 0; i < MAX; i++)  
57.          delete data[i];  
58.     print_table(data);  
59.      return 0;  
60.  }  
61.    
62.  //直接返回下标为key的元素  
63.  struct Hash* direct_address_search(struct Hash *T[], int key){  
64.      return T[key];  
65.  }  
66.    
67.   
68.  //直接将元素插入下标key的位置里  
69.    
70.  void direct_address_insert(struct Hash *T[], struct Hash *x){  
71.      T[x->key] = x;  
72.  }  
73.    
74.   
75.   // 将要删除的元素所在的位置指向空指针  
76.    
77.  void direct_address_delete(struct Hash *T[], struct Hash *x){  
78.      T[x->key] = NULL;  
79.  }  
80.    
81.   
82.  //打印直接寻址表  
83.   
84.  void print_table(struct Hash *T[]){  
85.      int i;   
86.      for(i = 0; i < MAX; i++){  
87.         if(T[i] != NULL){  
88.              printf("key is %d, and its satellite is %d\n", T[i]->key, T[i]->satellite);  
89.          }  
90.      }  
91.  }  

参考资料来自： 直接寻址表的字典操作

11.1-4我们希望在一个非常大的数组上，通过利用直接寻址的方式来实现一个字典。开始时，该数组中可能包含一些无用信息，但要对整个数组进行初始化是不太实际的，因为该数组的规模太大。请给出在大数组上实现直接寻址字典的方案。每个存储对象占用O(1)空间；SEARCH,INSERT和DELETE操作的时间均为O(1);并且对数据结构初始化的时间为O(1).(提示：可以利用一个附加数组，处理方式类似于栈，其大小等于实际存储在字典中的关键字数目，以帮助确定大数组中某个给定的项是否有效)

思路：我们用T表示大数组，用S表示含有所有有效数据的数组作为辅助栈。T的关键字作为下标，而数组T的值为数组S的下标，相反地，数组S的值为关键字，同时也是数组T的下标。这是一种循环形式 。设有关键字x，如果T[x]=y，那么S[y]=x.

[cpp]  view plain  copy

1. #include <iostream>  
2. using namespace std;  
3. #define MAX 100  
4. #define LEN sizeof(struct hash)  
5. struct hash{  
6.     int key;  
7. };  
8. struct Stack  
9. {  
10.     int STack[MAX];  
11.     int top;  
12. };   
13. void Init(struct Stack&s)  
14. {  
15.     s.top=-1;  
16. }  
17. struct hash * search(struct hash Hash[],struct Stack&s,int k)  
18. {  
19.     if (Hash[k].key>=0&&Hash[k].key<=s.top&&s.STack[Hash[k].key]==k)  
20.     {  
21.         cout<<"已经找到"<<endl;  
22.         return Hash+k;  
23.     }  
24.     else  
25.     {  
26.         cout<<"没有找到"<<endl;  
27.         return NULL;  
28.     }  
29. }  
30. void insert(struct hash Hash[],struct Stack&s,struct hash *x)  
31. {  
32.    int k=x->key;  
33.    if (search(Hash,s,k))  
34.    {  
35.        cout<<"待插入的数据已经在散列表中！"<<endl;  
36.        return ;  
37.    }  
38.    else  
39.    {  
40.        s.top++;  
41.        s.STack[s.top]=k;  
42.        Hash[k].key=s.top;  
43.    }  
44. }  
45. void Delete(struct hash Hash[],struct Stack&s,int k)  
46. {  
47.     struct hash *p=search(Hash,s,k);  
48.     if (!p)  
49.     {  
50.         cout<<"待删除的数据不在散列表中，无法删除"<<endl;  
51.         return;  
52.     }  
53.      s.STack[p->key]=s.STack[s.top];  
54.      Hash[s.STack[p->key]].key=p->key;  
55.      p->key=0;  
56.      s.top--;  
57. }  
58. void Print(struct Stack&s)    
59. {    
60.     int i;    
61.     if (s.top==-1)  
62.     {  
63.         cout<<"无数据可打印！"<<endl;  
64.         return ;  
65.     }  
66.     for(i = 0; i <= s.top; i++)    
67.         cout<<s.STack[i]<<' ';    
68.     cout<<endl;    
69. }   
70. void main()  
71. {  
72.     struct Stack s;  
73.     struct hash Hash[10000],*y;  
74.     Init(s);  
75.     char str;  
76.     int k=0;  
77.     while (1)  
78.     {  
79.         cout<<"A是插入B是删除C是查找D是打印E是退出"<<endl;  
80.         cin>>str;  
81.         if (str=='A')  
82.         {  
83.             y=new struct hash[LEN];  
84.             cin>>y->key;  
85.             insert(Hash,s,y);  
86.         }  
87.         if (str=='B')  
88.         {  
89.             cin>>k;  
90.             Delete(Hash,s,k);  
91.         }  
92.         if (str=='C')  
93.         {  
94.             cin>>k;  
95.             search(Hash,s,k);  
96.         }  
97.         if (str=='D')  
98.         {  
99.             Print(s);  
100.         }  
101.         if (str=='E')  
102.         {  
103.             break;  
104.         }  
105.     }  
106. }  

11.2散列表

多个关键字映射到同一个数组下标位置称为碰撞。

好的散列函数应使每个关键字都等可能地散列到m个槽位中。

链接法散列一次查找时间为O(1+a)  a=n/m.删除和插入的时间在下面练习中。

11.2-1假设用一个散列函数h将n个不同的关键字散列到一个长度为m的数组T中。假设采用的是简单均匀散列，那么期望的冲突数是多少？更准确地，集合{{k,l}:k≠l,且h(k)=h(l)}基的期望值是多少？

书中已经给出分析：E[X(kl)]=1/m

那么总的期望应该是E[∑∑E[X(kl)]]=∑∑1/m=n(n-1)/2m

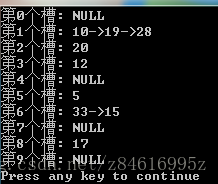
11.2-2 对于一个用链接法解决冲突的散列表，说明将关键字5,28,19,15,20,33,12,17,10,插入到该表中的过程。设该表中有9个槽位，并设其散列函数为h(k)=k mod 9.

[cpp]  view plain  copy

1. //11.2-2  
2. #include <iostream>  
3. using namespace std;  
4. #define MAX 10  //槽的个数  
5. #define LEN sizeof(struct list)  
6. struct list*head=NULL;  
7. struct list  
8. {  
9.     int key;  
10.     struct list*next;  
11.     struct list*prev;  
12. }slot[MAX];  
13. int hash(int y)  
14. {  
15.     int i=y%(MAX-1);  
16.     return i;  
17. }  
18. void Init(struct list *slot[])//初始化结构体数组  
19. {  
20.     for (int i=0;i<MAX;i++)  
21.     {  
22.         slot[i]=NULL;  
23.     }  
24. }  
25. //插入数据  
26. struct list*insert(struct list *slot[],struct list*x,int a[],int j)  
27. {  
28.     x=new struct list[LEN];  
29.     x->key=a[j];  
30.     int i=hash(x->key);  
31.     x->next=slot[i];  
32.     if (slot[i]!=NULL)  
33.     {  
34.         slot[i]->prev=x;  
35.     }  
36.     slot[i]=x;  
37.     x->prev=NULL;  
38.     return slot[i];  
39. }  
40. void Print(struct list *slot[])  
41. {  
42.     int i=0;  
43.     while (i!=MAX)  
44.     {  
45.         cout<<"第"<<i<<"个槽:"<<" ";  
46.         if (!slot[i])  
47.         {  
48.             cout<<"NULL";  
49.         }  
50.         while (slot[i])  
51.         {  
52.             cout<<slot[i]->key;  
53.             slot[i]=slot[i]->next;  
54.             if (slot[i])  
55.             {  
56.                 cout<<"->";  
57.             }  
58.         }  
59.         cout<<endl;  
60.         i++;  
61.     }  
62. }  
63. void main()  
64. {  
65.     struct list *slot[10*MAX],*x;  
66.     int a[9]={5,28,19,15,20,33,12,17,10};  
67.     Init(slot);  
68.     int i=0;  
69.     while (i!=9)  
70.     {  
71.         insert(slot,x,a,i);  
72.         i++;  
73.     }  
74.     Print(slot);  
75. }  

11.2-3 Marley教授做了这样一个假设，即如果将链模式改动一下，使得每个链表都能保持已排好序的顺序，散列的性能就可以有较大的提高。 Marley教授的改动对成功查找，不成功查找，插入和删除操作的运行时间有何影响？

对于一个总共有n个元素，m个槽的散列表来说，平均存储元素数为a=n/m。设Marley教授方法的所有排列都是非降序的。
查找操作：普通链接模式：由于插入时是无序的，所以查找时，成功的查找需要O(1+a1)时间(a1<a)。不成功查找也需要O(1+a)时间,因为遍历链表的时间是不稳定的。
                  有序链接模式：由于插入时是有序的，所以一次成功的查找时，一次成功查找平均需要O(1+a/2)时间。一次不成功的查找，平均时间也是O(1+a/2)。因为在查找过程中，都仅仅需要找到第一个大于等于k的元素为止，不需要遍历整个链表。假设链表中有序元素从1,2,....a依次排列，那么查找链表k元素平均时间就是O((1+a)/2)=O(a/2).所以总的时间为O(1+a/2)。所以查找时间减半了。
插入操作：普通链接模式：由于插入是不按照顺序的。所以只需要在表头插入即可。需要时间为O(1).
                  有序链接模式：由于插入是需要按照顺序的。所以要先找到插入位置。那么需要时间为O(1+a/2)。因为首先找到小于k的结点A，并且A的下一个结点大于k,然后插入到A的后面。所以插入操作的时间增加了。
删除操作：普通链接模式：利用双向链表仅用O(1)时间删除。但是删除前做一个元素是否存在的判断，那么就需要调用查找函数了。这样就需要O(1+a)时间了。
                 有序链接模式：利用双向链表仅用O(1)时间删除。如果同上一样要做判断，那么总时间就是O(1+a/2).所以删除操作时间减半了。
总结:查找与删除操作时间减半，插入操作时间增加了。



11.2-4 说明在散列表内部，如何通过将所有未占用的槽位链接成一个自由链表，来分配和释放元素所占的存储空间。假定一个槽位可以存储一个标志，一个元素加上一个或两个指针。所有的字典和自由链表操作均应具有O(1)的期望运行时间。该自由链表需要是双向链表吗？或者，是不是单链表就足够了呢？

        首先初始化一个自由表，该表能容纳散列表所有元素。然后和第十章链表的释放和分配内存类似，只不过由于要解决碰撞问题，散列需要一个指针数组来表示。对于这个自由链表需要用双向链表来提高插入，删除操作速度。

代码如下：

[cpp]  view plain  copy

1. //11.2-4 有自由表的散列表，自由表用来分配和释放内存的。  
2. #include <iostream>  
3. using namespace std;  
4. #define MAX 13  //槽的个数m  
5. #define max 100 //整个散列表的元素个数n  
6. #define LEN sizeof(struct list)  
7. struct list*Free=NULL;  
8. struct list * Allocate_object(struct list *x);//数组next为自由数组表  
9. void free_object(struct list *x);  
10. struct list  
11. {  
12.     int key;  
13.     int flag;  
14.     struct list*next;  
15.     struct list*prev;  
16. };  
17. int hash(int y)  
18. {  
19.     return y%MAX;  
20. }  
21. void Init(struct list *slot[])  
22. {  
23.     struct list *p,*p1;  
24.     for (int i=0;i<MAX;i++)//指针数组初始化  
25.     {  
26.         slot[i]=NULL;  
27.     }  
28.     for ( i=0;i<max;i++)//初始化自由表，该自由表也是一个双向链表。  
29.     {//自由表每个结点都是一个槽位，一个槽位包含1个key,1个flag和2个指针  
30.         p=new struct list[LEN];  
31.         p->flag=0;//0表示该结点无数据  
32.         if (Free==NULL)  
33.         {  
34.             p1=Free=p;  
35.         }  
36.         else  
37.         {  
38.             p1->next=p;  
39.             p->prev=p1;  
40.             p1=p;  
41.         }  
42.     }  
43.     p->next=NULL;  
44. }  
45. //查找数据  
46. struct list*search(struct list *slot[],int k)  
47. {//O(1+n/m)  
48.     int i=hash(k);//O(1)  
49.     struct list*x;  
50.     x=slot[i];  
51.     while (x!=NULL&&x->key!=k)//O(n/m) 如果散列表中槽和表中元素数成正比,有n=O(m)。那么运行时间就为O(1)。  
52.     {  
53.         x=x->next;  
54.     }  
55.     return x;  
56. }  
57. //插入数据  
58. struct list*insert(struct list *slot[],struct list*x)  
59. {  
60.     x=Allocate_object(x);  
61.     if (!x)  
62.     {  
63.         return NULL;  
64.     }  
65.     x->flag=1;//1表示有数据  
66.     x->key=rand()%max;  
67.     int i=hash(x->key);  
68.     x->next=slot[i];  
69.     if (slot[i]!=NULL)  
70.     {  
71.         slot[i]->prev=x;  
72.     }  
73.     slot[i]=x;  
74.     x->prev=NULL;  
75.     return slot[i];  
76. }  
77. //删除数据  
78. struct list*Delete(struct list *slot[],int k)  
79. {  
80.     int i=hash(k);  
81.     struct list *x=search(slot, k);  
82.     if (!x)  
83.     {  
84.         cout<<"待删除数据不存在！"<<endl;  
85.         return NULL;  
86.     }  
87.     if (x->prev!=NULL)  
88.     {  
89.         x->prev->next=x->next;  
90.     }   
91.     else  
92.     {  
93.         slot[i]=x->next;  
94.     }  
95.     if (x->next!=NULL)  
96.     {  
97.         x->next->prev=x->prev;  
98.     }  
99.     free_object(x);  
100.     cout<<"删除成功！"<<endl;  
101.     return slot[i];  
102. }  
103. //分配空间  
104. struct list * Allocate_object(struct list *x)//数组next为自由数组表  
105. {  
106.     if (Free==NULL)//表示未占用的槽  
107.     {  
108.         cerr<<"out of space"<<endl;  
109.         return NULL;  
110.     }  
111.     else  
112.     {  
113.         x=Free;  
114.         Free=Free->next;  
115.         return x;  
116.     }  
117. }  
118. //释放空间    
119. void free_object(struct list *x)  
120. {  
121.     x->flag=0;  
122.     x->next=Free;  
123.     Free=x;  
124. }  
125. void Print(struct list *slot[])  
126. {  
127.     int i=0;  
128.     while (i!=MAX)  
129.     {  
130.         cout<<"第"<<i<<"个槽:"<<" ";  
131.         if (!slot[i])  
132.         {  
133.             cout<<"NULL";  
134.         }  
135.         struct list *p=slot[i];  
136.         while (p)  
137.         {  
138.             cout<<p->key;  
139.             p=p->next;  
140.             if (p)  
141.             {  
142.                 cout<<"->";  
143.             }  
144.         }  
145.         cout<<endl;  
146.         i++;  
147.     }  
148. }  
149. void main()  
150. {  
151.     struct list *slot[10*MAX],*x;  
152.     Init(slot);  
153.     int i=0;  
154.     while (i!=max)  
155.     {  
156.         insert(slot,x);  
157.         i++;  
158.     }  
159.     Print(slot);  
160.     if(search(slot,0))  
161.     {  
162.         cout<<"已经找到"<<endl;  
163.     }  
164.     else  
165.     {  
166.         cout<<"没有找到"<<endl;  
167.     }  
168.     Delete(slot,89);  
169.     Delete(slot,26);  
170.     insert(slot,x);  
171.     insert(slot,x);  
172.     Print(slot);  
173. }  

11.2-5假设将一个具有n个关键字的集合存储到一个大小为m的散列表中。试说明如果这些关键字均源于全域U，且|U|>mn,则U中还有一个大小为n的子集，其由散列到同一槽位中的所有关键字构成，使得链接法散列的查找时间最坏情况下位θ(n).

       对于全域|U|>mn映射到m个槽中，若想U>mn,那么至少有一个槽位中的关键字大于n,其查找最坏时间为O(n)

11.2-6假设将n个关键字存储到一个大小为m且通过链接法解决冲突的散列表中，同时已知每条链的长度，包括其中最长链的长度L，请描述从散列表的所有关键字中均匀随机地选择某一元素并在O(L(1+1/a))的期望时间内返回该关键字的过程。

        如果整个哈希表有m行L列，每一行存储一条链。该数组有mL个位置存储这n个元素，并且有mL-n个空值。该程序随机选择数组中任意关键字，直到找到一个关键字并返回。成功的选择一个关键字的概率为n/mL,所以根据伯努利的几何分布知，需要经过mL/n=L/a次选择才能成功找到一个关键字。每次选择需要的时间是O(1)，所以成功选择一个关键字需要O(L/a),由于各链表的长度是已知的。这个最长链表L找到期望元素需要O(L)时间，所以从选择元素到找到元素需要O(L(1+1/a)).

11.3散列函数

（1）除法散列法：h(k) = k mod m

（2）乘法散列法：h(k) = m * (k * A mod 1) (0<A<1)

（3）全域散列：从一组散列函数中随机地选择一个,这样平均情况运行时间比较好。

11.3-1 假设我们希望查找一个长度为n的链表，其中每一个元素都包含一个关键字k并具有散列值h(k).每一个关键字都是长字符串。那么在表中查找具有给定关键字的元素时，如何利用各元素的散列值呢？

通过k的散列值h(k)对应的链表找到k.

11.3-2假设将一个长度为r的字符串散列到m个槽中，并将其视为一个以128为基数的数，要求应用除法散列法。我们可以很容易地把数m表示为一个32位的机器字，但对长度为r的字符串，由于它被当做以128为基数的数来处理，就要占用若干个机器字。假设应用散列法计算一个字符串的散列值，那么如何才能在除了该串本身占用的空间外，只利用常数个机器字。

对于每个字母分别取模然后求∑在取模 这一过程利用了模运算的性质，(a+b)%m=(a%m+b%m)%m

11.3-3考虑除法散列法的另一种，其中h(k)=k mod m,m=2^p-1,k为按基数2^p表示字符串。试证明，如果串x可由串y通过其自身的字符置换排列导出，则x和y具有相同的散列值。给出一个应用的例子，其中这一特性在散列函数中是不希望出现的。



比如录入英语单词时，mary是人名，而army是军队，两个单词如果都被用这种方式散列到同一个槽中，那么就会出现歧义。

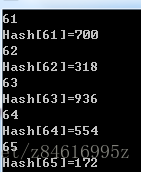
11.3-4 考虑一个大小为m=1000的散列表和一个对应的散列函数h(k)=m(kAmod1),其中A=(√5-1)/2,试计算关键字61,62,63,64和65被映射到位置。

[cpp]  view plain  copy

1. #include <iostream>  
2. #include <math.h>  
3. using namespace std;  
4. const double A=(sqrt(5)-1)/2.0;  
5. int hash(int k,int m)  
6. {  
7.     double x=(A*k-(int)(A*k))*m;  
8.     return x;  
9. }  
10. void main()  
11. {  
12.    int k;  
13.    while (cin>>k)  
14.    {  
15.        cout<<"Hash["<<k<<"]="<<hash(k,1000)<<endl;  
16.    }  
17. }  

11.3-5定义一个从有限集合U到有限集合B上的散列函数簇H为ε全域的。如果对U中所有的不同元素对k和l，都有 Pr{h(k)=h(l)}≤ε，其中概率是相对从函数簇H中随机抽取的散列函数h而言的。试证明：一个ε全域的散列函数簇必定满足：ε≥1/|B|-1/|U|

设b为|B|的槽个数，u为全域|U|的元素个数。

第j个槽中的元素数uj,其中发生冲突的元素对数为C(uj,2)=uj(uj-1)/2

第j个槽中最少有uj=u/b个元素在同一槽中。（《教师手册》里面有证明，这里略过）

所以总的冲突对数至少为∑uj(uj-1)/2=b(u/b)(u/b-1)/2。。。。(1)

而集合U中的元素对数总数是u(u-1)/2.....(2)

所以冲突对数概率ε≥(1)/(2)=(u/b-1)/(u-1)>(u/b-1)/u=1/b-1/u

所以一个ε全域的散列函数簇必定满足：ε≥1/b-1/u=1/|B|-1/|U|

11.3-6 设U为由取自Zp中的值构成的n元组集合，并设B=Zp,其中p为质数。当输入为一个取自U的输入n元组<a0, a1, …, an-1>时，定义其上的散列函数hb:U→B(b∈Zp)为：hb(<a0, a1, …, an-1>) = ∑(j=0~n-1, aj*b^j) 并且，设ℋ={hb:b∈Zp}.根据练习11.3-5中 ε全域的定义，证明 ℋ是((n-1)/p)全域的。(提示：见练习31.4-4)

      对于集合U上的两个互异的n元组 k=<k0, k1, …, kn-1> ϵ U, l=<l0, l1, …, ln-1> ϵ U, 其中ki != li, b ϵ Zp.U散列到B上发生碰撞的概率： Pr{hb(k) = hb(l)}= Pr{hb(k) – hb(l) = 0}= Pr{∑(j=0~n-1, (kj-lj)*b^j) = 0}.其中 ∑(j=0~n-1, (kj-lj)*b^j) = 0)是一个 n-1次的多项式方程，这个方程在Zp上的解b有至多n-1个根。所以Pr{∑(j=0~n-1, (kj-lj)*b^j) = 0} <= (n-1)/p, b ϵ Zp.Pr{hb(k) = hb(l)} <= (n-1)/p, b ϵ Zp.  ℋ 是((n – 1)/p)全域的。得证！参考资料： Rip's Infernal Majesty的博客

11.4开放寻址法

三种探查技术来计算探查序列：1)线性探查：h(k,i)=(h'(k)+i)mod m                i=0,1,1...,m-1

                                                   2)二次探查：h(k,i)=(h'(k)+c1i+c2i²) mod m   i同上

                                                   3)双重探查：h(k,i)=(h1(k)+ih2(k))mod m      i同上

开放寻址散列的分析：定理11.6 给定一个装载因子a=n/m<1的开放寻址散列表，在一次不成功的查找中，期望的探查数之多为1/(1-a).假设散列是均匀的。

推论11.7 平均情况，项一个装载因子为a的开放寻址散列表中插入一个元素时，至多需要做1/(1-a)次探查。假设采用的是均匀散列。

定理11.8 给定一个装载因子为a<1的开放寻址散列表，一次成功查找中的期望探查数之多为(1/a)ln(1/(1-a)).

在开放寻址法中，删除操作比较困难，但也有解决办法，不过在必须删除关键字的应用中，往往采用链接法解决碰撞。

以下是11.3-11.4节代码：

[cpp]  view plain  copy

1. //除法，乘法，全域散列。与 线性，二次，双重探查。  
2. #include <iostream>  
3. #include <math.h>  
4. #include <time.h>  
5. using namespace std;  
6. #define Null -1  
7. #define DELETED -2  
8. //除法散列  
9. int hash_div1(int k,int m)//选m的值常常是不接近2的幂的质数。  
10. {  
11.     return k%m;  
12. }  
13. //除法散列  
14. int hash_div2(int k,int m)//选m的值常常是不接近2的幂的质数。  
15. {  
16.     return k%m;  
17. }  
18. //乘法散列  
19. int hash_mul(int k)  
20. {  
21.    double A=(sqrt(5)-1)/2.0;  
22.    int m=100;//对于m没有特别要求。m一般选择为2的某个幂。  
23.    return (A*k-(int)(A*k))*m;  
24. }  
25. //全域散列 P为质数  
26. int hash_Universal(int k,int p)  
27. {  
28.     static int a=0,b=0,flag=0;  
29.     int m=6;//m不一定非是质数。  
30.     if (flag==0)  
31.     {  
32.         a=rand()%(p-1)+1;  
33.         b=rand()%p;  
34.         flag=1;  
35.     }  
36.     return ((a*k+b)%p)%m;  
37. }  
38. //线性探查  
39. int LineProbe(int k,int m,int i)  
40. {  
41.     return (hash_div1(k,m)+i)%m; //选m的值常常是不接近2的幂的质数。  
42. }  
43. //二次探查    
44. int QuadraticProbing(int k,int m,int i)    
45. {    
46.     int c1=1,c2=3;      
47.     return (hash_div1(k,m)+c1*i+c2*i*i)%m; //其中常数c1,c2,m的值的选择是受限制的   
48. }    
49. //双重探查    
50. int DoublefunProbing(int k,int m,int i)    
51. {    
52.     return (hash_div1(k,m)+i*(1+hash_div2(k,m-1)))%m; //其中m为质数，还可以选择m为2的幂,并设置一个总产生奇数的hash_div2  
53. }    
54. int hash_insert1(int T[],int m,int k)  
55. {  
56.     int i=0;  
57.     do   
58.     {  
59.         int j=LineProbe(k,m,i);//这里可以替换成二次，双重探查。插入，查找，删除函数同时被替换  
60.         if (T[j]==Null||T[j]==DELETED)  
61.         {  
62.             T[j]=k;  
63.             return j;  
64.         }  
65.         else i++;  
66.     } while (i!=m);  
67.     cerr<<"hash table overflow"<<endl;  
68. }  
69. int hash_insert2(int T[],int m,int k)  
70. {  
71.     int i=0;  
72.     do   
73.     {  
74.         int j=QuadraticProbing(k,m,i);//这里可以替换成二次，双重探查。插入，查找，删除函数同时被替换  
75.         if (T[j]==Null||T[j]==DELETED)  
76.         {  
77.             T[j]=k;  
78.             return j;  
79.         }  
80.         else i++;  
81.     } while (i!=m);  
82.     cerr<<"hash table overflow"<<endl;  
83. }  
84. int hash_insert3(int T[],int m,int k)  
85. {  
86.     int i=0;  
87.     do   
88.     {  
89.         int j=DoublefunProbing(k,m,i);//这里可以替换成二次，双重探查。插入，查找，删除函数同时被替换  
90.         if (T[j]==Null||T[j]==DELETED)  
91.         {  
92.             T[j]=k;  
93.             return j;  
94.         }  
95.         else i++;  
96.     } while (i!=m);  
97.     cerr<<"hash table overflow"<<endl;  
98. }  
99. int hash_search(int T[],int m,int k)  
100. {  
101.     int i=0,j=0;  
102.     do   
103.     {  
104.         j=LineProbe(k,m,i);//这里可以替换成二次，双重探查。插入，查找，删除函数同时被替换  
105.         if (T[j]==k)  
106.         {  
107.             return j;  
108.         }  
109.         else i++;  
110.     } while (T[j]!=Null||i!=m);  
111.     return Null;  
112. }  
113. void hash_delete(int T[],int m,int k)  
114. {  
115.     int j=hash_search(T,m,k);//首先先找到该关键字k  
116.     if (j!=Null)  
117.     {  
118.        T[j]=DELETED;//如果找到了，那么设置其为空。  
119.        cout<<"删除成功！"<<endl;  
120.     }  
121.     else cout<<"待删除的数据不在表中！"<<endl;  
122. }  
123. int main()    
124. {    
125.     srand( (unsigned)time( NULL ) );  
126.     int a[9]={10,22,31,4,15,28,17,88,59};    
127.     int T[11]={0};   
128.     cout<<"线性散列="<<endl;  
129.     for (int i=0;i<11;i++)  
130.     {  
131.         T[i]=Null;  
132.     }  
133.     for( i=0;i<9;i++)    
134.     {    
135.         hash_insert1(T,11,a[i]);    
136.     }    
137.     for(i=0;i<11;i++)    
138.     {     
139.         cout<<T[i]<<" ";     
140.     }   
141.     cout<<endl;  
142.     cout<<"二次散列="<<endl;  
143.     for (i=0;i<11;i++)  
144.     {  
145.         T[i]=Null;  
146.     }  
147.     for( i=0;i<9;i++)    
148.     {    
149.         hash_insert2(T,11,a[i]);    
150.     }    
151.     for(i=0;i<11;i++)    
152.     {     
153.         cout<<T[i]<<" ";     
154.     }   
155.     cout<<endl;  
156.     cout<<"双重散列="<<endl;  
157.     for (i=0;i<11;i++)  
158.     {  
159.         T[i]=Null;  
160.     }  
161.     for( i=0;i<9;i++)    
162.     {    
163.         hash_insert3(T,11,a[i]);    
164.     }    
165.     for(i=0;i<11;i++)    
166.     {    
167.          cout<<T[i]<<" ";     
168.     }    
169.     cout<<endl;    
170.     cout<<hash_search(T,11,31)<<endl;    
171.     hash_delete(T,11,31);    
172.     cout<<hash_search(T,11,31)<<endl;    
173.     return 0;  
174. }    

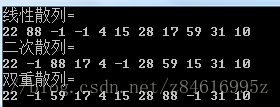
11.4-1 考虑将关键字10,22,31,4,15,28,17,88,59用开放寻址法插入到一个长度为m=11的散列表中，主散列函数为h'(k)=k mod m.说明用线性探查，二次探查(c1=1,c2=3)以及双重散列h2(k)=1+(k mod (m-1))将这些关键字插入散列表的结果。

用11.3-11.4节代码可得：

11.4-2请写出HASH-DELETE的伪代码；修改HASH-INSERT,使之能处理特殊值DELETED。



见11.3-11.4节代码。

11.4-3 假设采用双重散列来解决碰撞；亦即，所用的散列函数为h(k,i)=(h1(k)+h2(k))mod m.证明：如果对某个关键字k,m和h2(k)有最大公约数d≥1，则在对关键字k的一次不成功的查找中，在回到槽h1(k)之前，要检查散列表的1/d.于是，当d=1时，m与h2(k)互质，查找操作可能要检查整个散列表。(提示：见第31章)

      设经过s次查找后，回到槽h1(k)。那么就有(h1(k)+sh2(k))mod m=h1(k)mod m 。此时sh2(k)是m的倍数=> m|sh2(k) 由于gcd(m,h2(k))=d => (m/d) | s(h2(k)/d) 由于gcd(m/d,h2(k)/d)=1 => m/d | s =>s≥m/d=>所以在回到槽h1(k)之前，必检查散列表总元素数的1/d.(更具体地讲应该是至少1/d个) 。当d=1时，1/d=1,所以可能要检查整个散列表。

11.4-4考虑一个采用了均匀散列的开放寻址散列表。给出当装载因子为3/4和7/8时，在一次不成功查找中期望探查数的上界，以及一次成功查找中期望探查数的上界。

 不成功的探查上界为1/(1-a):  1/(1-3/4)=4次      1/(1-7/8)=8次                              成功的探查上界为(1/a)ln(1/(1-a)):  1/(3/4)ln(1/(1-3/4))=1.848次   1/(7/8)ln(1/(1-7/8))=2.377次

11.4-5 考虑一个装载因子为a的开放寻址散列表。找出一个非0的值a，使得在一次不成功的查找中，期望的探查数等于成功查找中期望探查数的两倍。此处的两个期望探查数上界可以根据定理11.6和定理11.8得到。

        不成功探查：1/(1-a)   成功探查：(1/a)ln(1/(1-a))   1/(1-a)=2(1/a)ln(1/(1-a)) 关于a的解为：a≈0.715

11.5完全散列

      定义：在使用链接法的1级散列产生冲突后，在每个冲突的槽再次用较小的2级散列，经过随机多次的2级散列筛选后，从而达到2级散列表不发生冲突的目的。

11.5-1 假设要将n个关键字插入到一个大小为m,采用了开放寻址法和均匀散列基数的散列表中。设p(n,m)为没有碰撞发生的概率。证明：p(n,m)≤e^[-n(n-1)/2m].(提示：见公式3.11)论证当n超过√m时，不发生碰撞的概率迅速趋于0.

     对于这n个关键字，有C(n,2)对关键字可能发生碰撞，而每一对关键字对于m个槽发生碰撞的概率是1/m。所以对于n个关键字总共有C(n,2)/m概率发生碰撞，那么p(n,m)=1-C(n,2)/m=1-n(n-1)/2m≤e^[-n(n-1)/2m].(根据1+x≤e^x).后面那个问题不清楚，网上也没有相关答案。

11-1最长探查的界

      用一个大小为m的散列表来存储n个数据项目，并且有n≤m/2。采用开放寻址法来解决碰撞问题。

      a)假设采用了均匀散列，证明对于i=1,2,....n,第i次插入需要严格多于k次探查的概率至多为2^(-k).

        p(x>k)=p(x≥k+1)=(n/m)((n-1)/(m-1)).....(n-k+1)/(m-k+1)≤(n/m)^k≤2^(-k)  利用的是定理11.5分析方法。

          b) 证明：对于i=1,2...n,第i次插入需要多于2lgn次探查的概率至多是1/n^2.

        当k=2lgn时，带入a式便得到p(x>2lgn)≤1/n^2

设随机变量Xi表示第i次插入所需的探查数。在上面b中已经证明Pr{Xi>2lgn}≤1/n^2.设随机变量X=maxXi表示n次插入中所需探查数的最大值。

      c)证明：Pr{X>2lgn}≤1/n

       设事件Xi发生的概率为P{Ai},那么事件X1或事件X2或。。。。时间Xn发生的概率为P{X1∪X2...∪Xn}≤P{X1}+P{X2}+......P{Xn}

由于事件X为探查数最大值，所以事件Xi中成为事件X=X1∪X2...∪Xn,根据b式有P{Xi}≤1/n^2,所以P{X1∪X2...∪Xn}≤n*(1/n^2)=1/n

         d)证明：最长探查序列的期望长度为E[x]=O(lgn)

        根据期望的定义：E[x]=∑(k=1~n)kPr{X=k}

                                           =∑(k=1~2lgn)kPr{X=k}+∑(k=2lgn+1,n)kPr{X=k}

                                           =∑(k≤2lgn)kPr{X=k}+∑(k≥2lgn+1)kPr{X=k}

                                           ≤∑2lgnPr{X=k}+∑nPr{X=k}

                                           =2lgnPr{X≤2lgn}+nPr{X>2lgn} 其中Pr{X≤2lgn}≤1，根据b式Pr{X>2lgn}≤1/n^2 E[x]≤2lgn*1+n*(1/n^2)≤2lgn*1+n*(1/n)=O(lgn) d式参照《教师手册》

11-2 链接法中槽大小的界

             假设有一个含n个槽的散列表，并用链接法来解决碰撞问题。另假设向表中插入n个关键字。每个关键字被等可能地散列到每个槽中。设在所有关键字被插入后，M是各槽中所含关键字数的最大值。读者的任务是证明M的期望值E[M]的一个上界为O(lgn/lglgn).

             a)论证k个关键字被散列到某一特定槽中的概率Qk为：Qk=(1/n)^k(1-1/n)^(n-k)C(n,k)

                这个概率可以抽象成：有C(n,k)种方法选出n次试验中哪k次成功。被散列到特定槽X0视为成功，其成功率是1/n，相反则视为失败概率为1-1/n. 那么根据伯努利的二项分布就是a的答案。

        b)设Pk为M=k的概率，也就是包含最多关键字的槽中k个关键字的概率。证明：Pk≤nQk.

               同思考题11-1c式被散列到槽中最多的关键字数视为一个事件X=X1∪X2∪....∪Xn，其中Xi为被散列到槽i的事件。所以根据布尔不等式Pr{X}≤Pr{X1}+Pr{X2}+....+Pr{Xn}=nQk

             c)应用斯特林近似公式，证明Qk<e^k/k^k 

                Qk=(1/n)^k(1-1/n)^(n-k)C(n,k)<n!/(n^k)k!(n-k)!   (根据(1-1/n)^(n-k)<1)

                                                               <1/k!                     (根据n!/(n-k)!<n^k)

                                                               <e^k/k^k               (根据斯特林近似式k!>(k/e)^k)

             d) 没看懂《教师手册》证明！

              e)论证：E[M]≤Pr{M>clgn/lglgn}*n+Pr{M≤clgn/lglgn}*clgn/lglgn并总结：E[M]=O(lgn/lglgn)

             这个和思考题11-1d证明完全一样，方法往上看11-1d。

11-3 二次探查

            假设要在一个散列表(表中的各个位置为0,1.。。m-1)中查找关键字k,并假设有一个散列函数h将关键字空间映射到集合{0,1,...,m-1}上，查找方法如下：

1) 计算值i←h(k),置j←0。

2)探查位置i,如果找到了所需的关键字k,或如果这个位置是空的，则结束查找。

3)置j←(j+1)mod m,i←(i+j) mod m,返回步2).

            设m是2的幂。

             a)通过给出等式(11.5)中c1和c2的适当值，来证明这个方案是一般的“二次探查”法的一个实例。

               由j=0~m-1得每次循环j就自加1，于是有j=1~m, 初始时，i=h(k),所以第j次循环i=h(k)+1+2..+j=h(k)+j²/2+j/2. 其中当c1=1/2, c2=1/2.

        b)证明：在最坏情况下，这个算法要检查表中的每一个位置。

                哎~ 这个比较坑爹！因为涉及了数论知识。不懂数论的可以略过了。

              在这个算法中，从j=0到m循环中，假设有第i次循环与第j次循环所得散列值h(k,i)=h(k,j)的情况( 且0<i<j<m.) h(k,i)=(h(k)+i²/2+i/2)mod m  h(k,j)=(h(k)+j²/2+j/2)mod m。所以h(k,i)与h(k,j)同余。同余式可表示为(h(k)+i²/2+i/2)≡(h(k)+j²/2+j/2)mod m  <=>(j²/2+j/2-i²/2-i/2)≡0(mod m)  <=>(j-i)(j+i+1)/2≡0(mod m) <=>(j-i)(j+i+1)/2=mk <=>由于m为2的幂。所以设m=2^t.   (j-i)(j+i+1)=k*2^(t+1).........①

              现在论证j-i与j+i+1若一个为奇数，则另一个必为偶数....②  若i=2k1,j=2k2,则j-i=2(k2-k1)为偶数，i+j+1=2(k1+k2)+1为奇数，类似地：i与j都为奇数或i与j一奇一偶都可以证明②式。

              现在假设j-i为奇数，那么j+i+1为偶数，gcd(2^(t+1),j-i)=1.由①式知：2^(t+1) | (j-i)(j+i+1)  所以根据推论31.5：2^(t+1) | (j+i+1).由于j+i+1≤m-1+m-2+1=2(m-1)<2m=2^(t+1) 所以2^(t+1) 不能整除(j+i+1)，同理j-i为偶数与j+i+1为奇数时，2^(t+1) 不能整除(j-i).所以①式不成立。所以h(k,i)≠h(k,j),在循环0~m中，任意i与j的hash值都不相等，那么这m次循环得到的hash值各不相等，所以共有m个不同的hash值对应表中m个关键字，覆盖了整个散列表。

11-4 题目没读懂，不知从何下手！