一位原码乘法的计算

(1)数学原理：   

                两个原码数相乘,其乘积的符号为相乘两数符号的异或值,数值等于两数绝对值之积。  

                 假设 [X]原=X0.X1X2..Xn ，           

                 [Y]原=Y0.Y1Y2..Yn，

          则有：   [X·Y]原= (X0⊕Y0).[(X1X2..Xn)·(Y1Y2..Yn)]

(2)算法：

         假设 X=0.X1X2..Xn ，Y=0.Y1Y2..Yn，

          即均为正纯小数   X·Y= X·0.Y1Y2..Yn     

                          = X·（2-1Y1+2-2Y2+...+2-n+1Yn-1+2-nYn）     

                          = X·（2-nYn+2-n+1Yn-1+...+2-2Y2+2-1Y1）      

                          = (..((0+ Yn X)2-1+Yn-1X)2-1)+...)+Y2X)2-1)+Y1X)2--1)  

                  根据上述计算过程，

             

                 可得算法如下：      

                    A0=0      

                   A1=（A0+YnX)2-1      

                   A2=（A1+Yn-1X)2-1    

                              ...     

                   An-1=（An-2+Y2X)2-1      

                   An  =（An-1+Y1X)2-1    

                 积X·Y=An

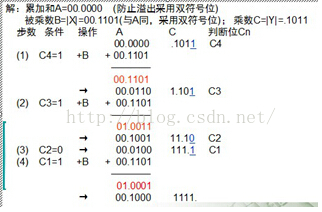
例如1：

      X =0.1101 ， Y = -0.1011求 Y * Y

   如图计算过程：

例如2：

      X = -0.1011, Y = -0.0110 求（Y * Y）的原码

计算过程如下：