支持向量机是与统计机器理论相关的机器学习算法,在1992年首次引入。SVM之所以流行,源于其对手写数字识别的错误率达到1.1%,与一个精确构建的神经网络的错误率相当。SVM现在被认为是kernel methods里面的一个经典例子。
一、 分类问题
1. 问题的提出
问题:给定训练集,其中
;
目标:学习一个分类函数g(x),使得f(x) = sign(g(x))能对新输入的x进行分类
线性分类器:
对于一个线性可分的二分类问题,我们可以找到很多的分类界面,如下图所示:
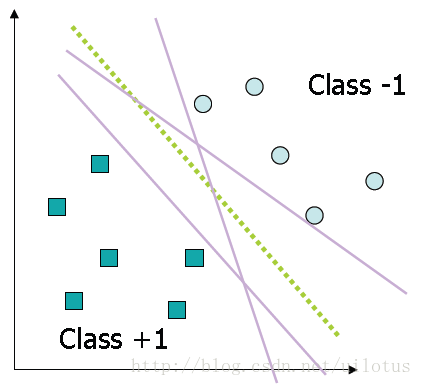
很多人提出了不同的算法寻找分类界面,Perceptron算法只能找到一个这样的分类界面,但是不同的判别界面是否一样好呢?答案是显然的。
2. 基于平分线的决策界面(Bisector based Decision Boundary)
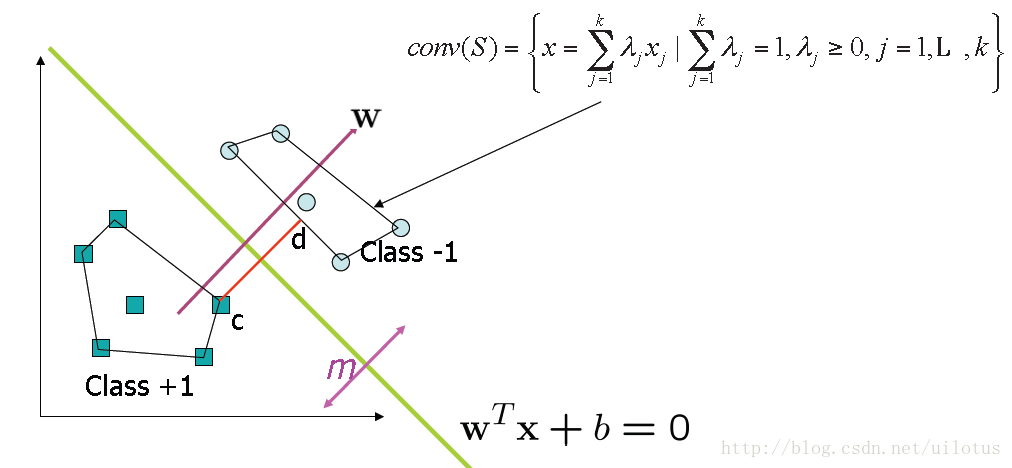
对于线性可分的二分类问题,我们将每一类的全部点构成一个凸集,
如上图所示,我们的目标是找到两个凸集之间距离最近的两个点c和d,在这个两个点之间连一条直线cd,然后以这条线段cd的垂直平分线做为判别界面。
Formalization:
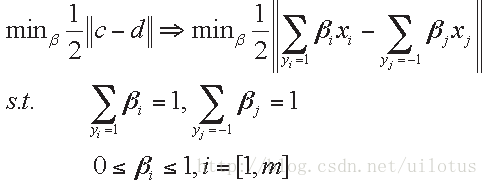
我们的目标是求得使上式最小的β,这样我们就能得到c和d:
然后求得c和d连线的中垂线:
其中:
这样我们就可以通过来对样本点进行分类。
二、 最大间隔界Maximal Margin
1. 线性可分的情况:
1) 最大间隔界
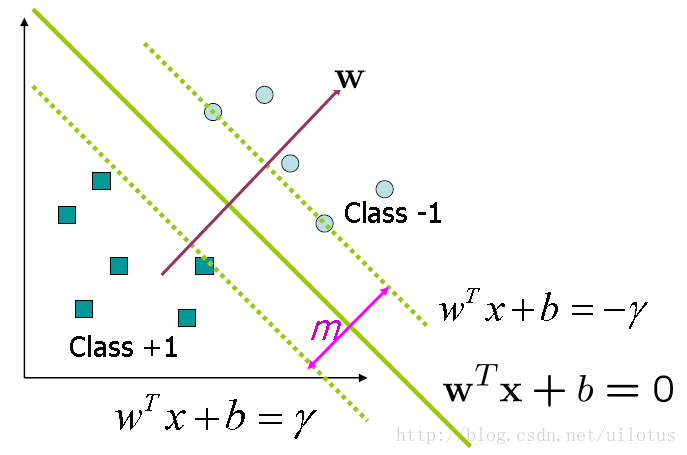
直观上来讲,分类界面应该离两类点的距离尽量远,这样的话,我们需要找到两类点之间的最大间隔,以此为基础选择分类界面。
如图所示,依据原点到直线的距离公式,我们可以得到两类点之间间隔的表达式
我们希望最大化这个间隔
约束条件:
由于我们可以同时放大和缩小w和b的值而不改变,我们可以调整w和b的值,使得γ = 1,那么问题可以做如下转换:
于是我们得到一个优化目标:
2)求解:
对于上面的优化问题,我们可以写出等价的拉格朗日形式:
首先我们先看一下对于一般的拉格朗日函数的求解:
我们先定义一个函数
如果约束条件不被满足的话,我们得到
当约束条件被满足的时候,我们可以得到
于是我们得出:
这样原优化问题就等价于:
他的对偶问题是:
我们可以推导出原问题和对偶问题有如下的关系:
那么在什么样的条件下我们可以得到d = p 呢?
这就需要用到KKT条件(Karush-Kuhn-Tucher):
回到我们的问题:
其拉格朗日形式为:
我们的问题就可以转化为求解:
其对偶问题是:
通过求解里面的最小化问题得到:
于是我们有:
带回L化简之后得到:
这样对偶问题就变成了求解如下优化问题:
这是一个二次优化问题,我们总能找到最优解 α, 然后可以得到:
以及
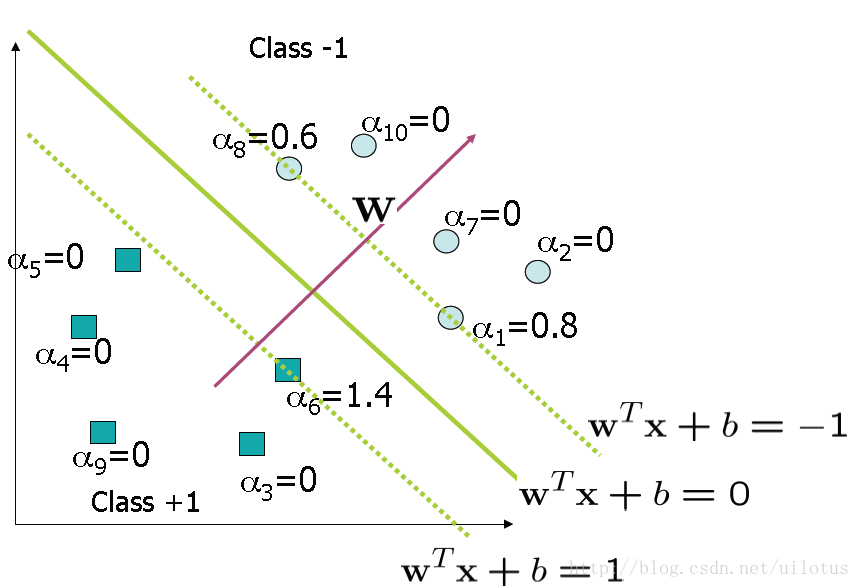
3)说明:
a、由于许多的α 值都为0, 由上面w的表达式可以知道,w是少量数据样本的线性组合,这种稀疏的表示方法可以看做一种数据压缩。
b、对于α 值非0 的点,我们称其为支持向量,分类的决策面就是由支持向量决定的。
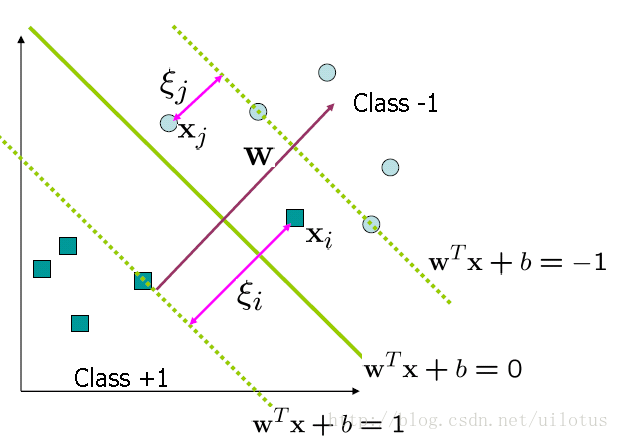
2. 线性不可分的情况:
之前的讨论仅仅适用于线性可分的情况。样本线性不可分的情况下,我们引入了松弛变量
这里,我们允许间隔小于1,对于小于1的间隔1-ε,我们在目标函数中增加一个cost,C*ε, C控制着w和ε之间的权重比例。
对应的拉格朗日形式为:
得到min max问题的对偶问题max min问题,我们对于min L求解之后得到
这是个二次优化问题,求解同上。
最后按照 α 值的不同范围,我们得到如下结论:
当 α = 0时, 为正确分类的样本;
当 α = C 时,为可能误分的样本点;
当 0 < α < C时, 为支持向量.








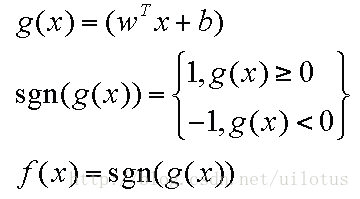
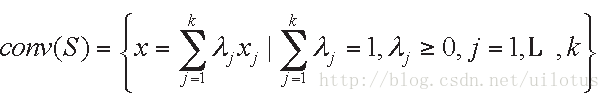


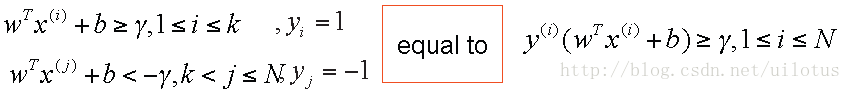
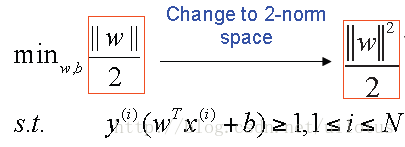
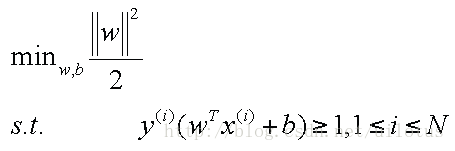
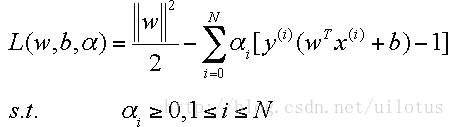
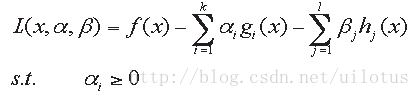
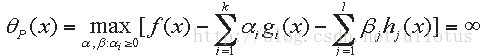
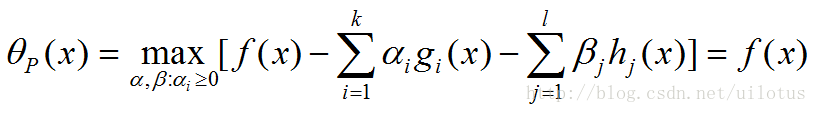

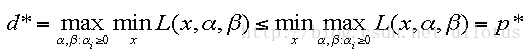
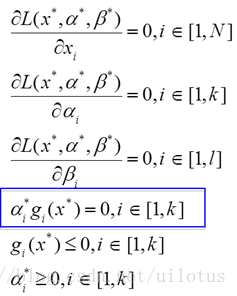
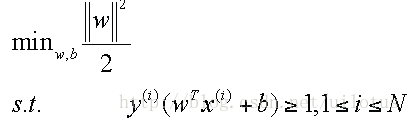
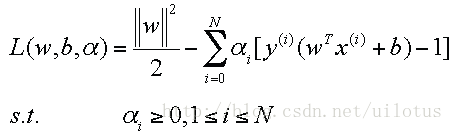
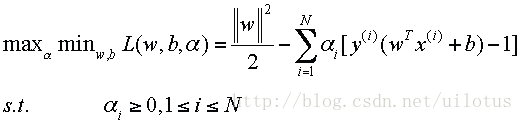
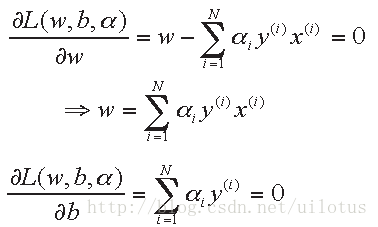
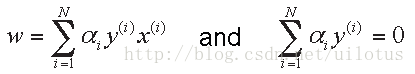
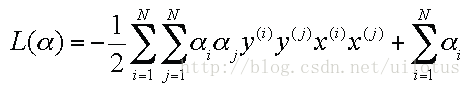
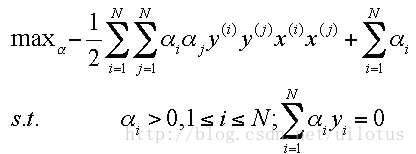
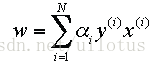
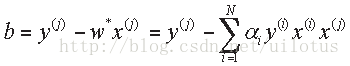
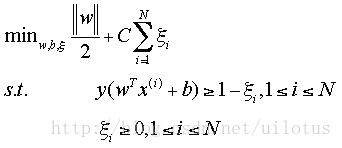
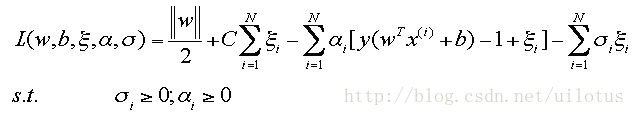
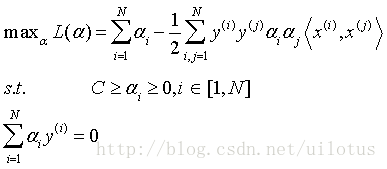
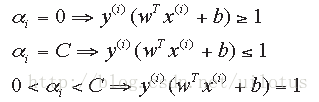













 3534
3534











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








