一、 雇佣问题
问题:雇用一名新的办公室助理,雇用代理每天给你推荐一个应聘者,面试和雇用都需要费用,但雇用的费用更高,预测费用。
策略:假设应聘者编号为1到n面试完应聘者i之后,如果i是到目前为止你见过的最适当人选,则雇用i。
Hire-Assistant(n)
1 best<--0
2 for i<--1 to n
3 if candidate i is better than candidate best
4 then best<--i
5 hire candidate ia. 最坏情况分析:应聘者以资质递增的顺序出现,则m = n。
b . 概率分析:不知道出现的顺序也无法控制;假设以随机的顺序出现,每种出现顺序是等可能的, 然后分析算法计算一个期望运行时间;实际上是将所有可能数据的运行时间平均, n!种可能等可能出现。
随机算法:如果一个算法的行为不仅仅是由输入决定的,同时也由随机数生成器所产生的数值决定,则称这个算法是随机的。
二、 指示器随机变量:
1. 定义: 给定一个样本空间S和事件A,那么事件A所对应的指示器随机变量I{A}定义为
2. 引理:给定样本空间S和S中的事件A,令XA = I{A},则E[XA]= Pr{A}。
即:事件A对应的指示器随机变量的期望值等于事件A发生的概率。
3. 利用指示器随机变量分析雇用问题:
假设应聘者以随机的顺序出现, X为雇佣次数,令Xi为第i个应聘者被雇佣的指示器随机变量,
由于假设随机的顺序,所以前i个任何一个都等可能是目前最有资格的,因此E[Xi]=1/i。
E(X) = E(X1 + X2 + ... + Xn) = 1 + 1/2 + 1/3 + ... + 1/n = ln n + O(1).
因此,由调和级数,大约只雇佣了ln n个人。
引理: 假设应聘者以随机的次序出现,算法HIRE-ASSISTANT总的雇佣费用为O(Ch*ln n)
三、 随机算法
引入:很多时候无法知道输入的有关信息,有一种做法是对输入进行控制,增加随机性:
a、 并不改变期望值;
b、 依赖于随机的选择;
c、 对所有的输入都是同样的期望值。
随机性发生在算法上,而不是发生自输入的分布上。
Randomized-Hire-Assistant(n)
1 randomly permute the list of candidates
2 best<--0
3 for i<--1 to n
4 if candidate i is better than candidate best
5 then best<--i
6 hire candidate i1. 随机排列数组:算法一
输入:一个数组A,它包含元素1到n
输出:数组的一个随机排列
算法一:给每个元素A[i]赋一个随机的优先级P[i],然后依据优先级对数组A中的元素进行排序。
Permute-by-Sorting(A)
1 n<--length[A]
2 for i <- 1 to n
3 do P[i] = Random(1, n^3)
4 sort A using P as sort keys
5 return A引理:假设所有优先级唯一,上述算法可以产生一个均匀随机排列。
[注意]每个元素A[i]处于位置j的概率是1/n并不能推出排列是均匀随机排列。
2. 随机排列数组:算法二 将A[i~n]中的值随机选一个置于A[i]
Randomize-In-Place(A)
1 n<--length[A]
2 for i <-- 1 to n
3 do swap A[i]<-->A[Random(i, n)]证明:定义循环不变式,算法每次迭代之前,对于每个可能的i-1排列,数组包含这个i-1排列的概率是(n-i+1)!/n!
此循环不变式成立,终止时,i = n + 1,可知对于任何排列,出现的概率是 1/n!.
四、 应用
1. 生日悖论
一个房间里的人数必须要达到多少,才能使有两个人生日相同的概率达到50%,假设每年n(365)天。
解法一:概率分析,假设人数为n,我们来计算每个人的生日都不同的概率
p = n*(n-1)*(n-2)*...*(n-m+1) / n^m = 1 * (1-1/n) * (1-2/n) * (1-3/n) * ... * (1-(m-1)/n)
由于 1+ x <= e^x
p = 1 * e^(-1/n) * e^(-2/n) * ... * e^(-(m-1)/n) = e^(-1/n - 2/n - 3/n -... - (m-1)/n) = e^(-m*(m-1)/2n) <= 0.5 = e^ln2
即: - m * (m - 1)/2n <= ln2
由此可解得m的值。
当n = 365, k ≥ 23.
解法二: 利用指示器随机变量来分析
定义指示器随机变量
两个人生日相同的概率为n*(1/n)*(1/n)=1/n
所以E(Xij) = 1/n
令X表示具有相同生日的两人对数目,则
对n = 365,k = 28时,X期望值为1
注: 与前一种准确数目不等,但渐近意义上是相等的,都是Θ(sqrt(n)),渐进分析对n很大时才有意义。
2. 球与盒子
问题:把相同的球随机投到b个盒子里,在每个盒子都有球之前,要投多少个球(每次投都会到一个盒子里!)
解答:定义“击中”为球落在空盒子里面,定义第 i 阶段为从第 (i-1) 次击中到i次击中之间的投球。第 i 阶段,投球击中的概率为 (b-i+1)/b, 因此投球数 ni 的期望为E[ni] = b/(b-i+1),所以,总的投球数期望为
因此在我们期望每个盒子里都有一个球之前,大约要投blnb次 。
注:a、盒子问题也成为赠卷收集者问题:一个人要想集齐b种不同赠卷中的每一种,大约要有blnb张随机得到的赠卷才能成功。
b、在给定的盒子里至少有一个球之前,平均至少要投多少个球?要投的个数服从几何分布,概率为1/b,成功的期望个数是1/(1/b)=b。
c、有多少球落在给定的盒子里?落在给定盒子里的球数服从几何分布,如果投n个球,落在给定盒子中的球数的期望值是n/b。
3. 序列
问题:抛一枚均匀硬币n次,期望看到连续正面的最长序列有多长?
解法一:定义Aik为长度至少为k的正面序列开始于第i次抛掷,即第i,i+1,…,i+k-1次硬币是正面,所以有Pr{Aik} = 1/ 2^k
对于k = 2ceil(log n)
因此, 长度至少为2ceil(log n)的一个起始于位置i的正面序列概率是很小的
而长度至少为2ceil(log n)的起始于任意位置的正面序列的概率是:
定义Lj:最长正面序列长度正好是j的事件(不相交)
假设最长序列的长度是L
对于r >= 1, 由长度为r*ceil(logn)的正面组成的序列开始于位置i的概率为:
因此,最长序列>=r*ceil(logn)的概率最多为n/n^r = 1/ n^(r-1)
即最长序列长度小于r*ceil(logn)的概率至少为1-1/ n^(r-1)。
我们令len = floor((log n)/2),将连续的n次投掷分成至少 floor(n / len)组,每组len次投掷
那么,从位置i开始的整个组都是正面的概率为
则整个组不是全正面的概率为 <= 1- 1/sqrt(n);
一共有floor(n / len)个组,每个组是相互独立的,所以每个组都不是全正面的概率至多为
至少有一个全正面的情况,即最长序列超过len的概率为
解法二:利用指示器随机变量来分析
设Xik = I{Aik}:序列长度至少为k的序列开始于第i次抛硬币的指示器随机变量,
定义X = ΣXik,也即最长序列长度 > k
设 k = c logn,于是有
说明:a、如果c比较大,长为clgn的序列期望就很少
b、如果c<1/2, E(x) = Θ(1/sqrt(n))
c、 于是可以粗略的估计:最长序列期望长度是Θ(logn)
4. 在线雇用问题
问题: 假设现在不想面试所有的人而且只想雇佣一次,于是给每个面试者i打不相同的分score(i),并采用如下策略:
选择一个正整数k<n,面试前k个应聘者并拒绝他们,再雇佣其后比前面所有应聘者分数更高的第一个应聘者,如果没有这样的人,雇佣第n个应聘者。
解答:算法如下
Online-Maxium(k, n)
1 bestScore <-- -INF
2 for i <-- 1 to k
3<span style="white-space:pre"> </span>do if bestScore < score(i)
4<span style="white-space:pre"> </span> then bestScore <-- score(i)
5 for i <-- k+1 to n
6 do if bestScore < score(i)
7 <span style="white-space:pre"> </span>then return i
8 return n b、 概率最高的k值可以用来最好的实现这个策略;
c、 K太小太大雇用到最好应聘者的概率都不高。
设S是我们成功选择的是最好应聘者的事件,Si表示最好的应聘者是第i个面试者时成功的事件,则
设Bi表示最好的应聘者在第i个位置上的事件,Pr{Bi}=1/n
注:Bi != Si,因为Si表示的是我们在位置i成功选择了最好应聘者,Bi表示的是真正最好的应聘者在第i个位置,在第K+1到i-1中可能有比第1到k个中最好的还好的应聘者,这样仅发生Bi未必Si也发生,所以两者不等。
设Oi表示k+1到i-1中没有应聘者被选取的事件,即当k+1≤j≤i-1时,score(j)<bestscore,此事件仅取决于1到i-1的排列情况,与Bi是独立事件。
前i-1个应聘者分数最高的可以是前K个中的任意一个位置,所以Pr{Oi}=k/(i-1)
要想雇用到第i个应聘者(Si)且为最佳应聘者,必须同时有发生Bi和Oi:
我们希望最大化成功概率,因而主要关注如何选取k的值,使其能最大化Pr{S}的下界:
上式左侧当k = n/e时取最大值1/e,即如果用k=n/e来实现我们的策略,则可以以至少1/e的概率成功雇用到最有资格的应聘者。









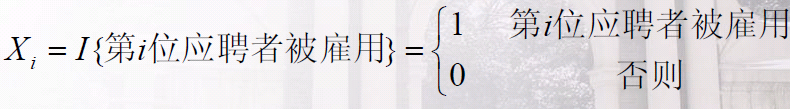
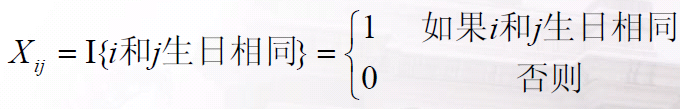
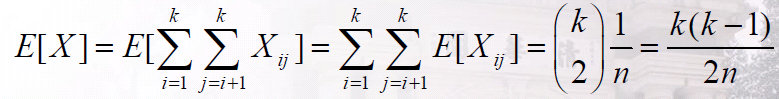
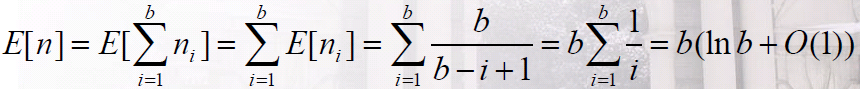
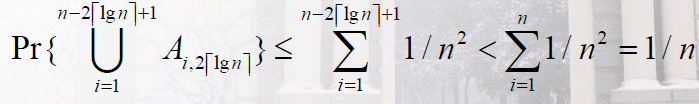
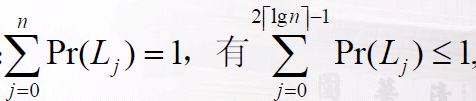
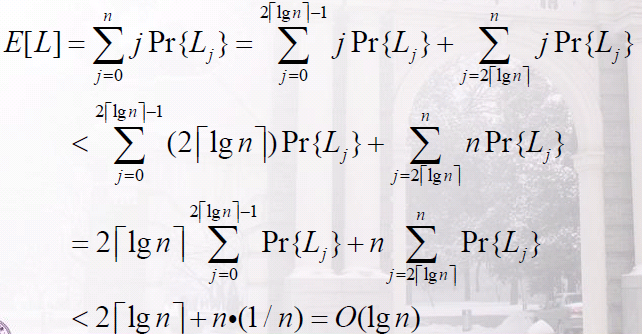
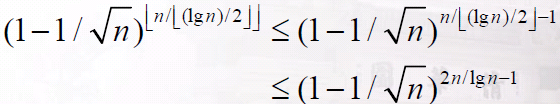
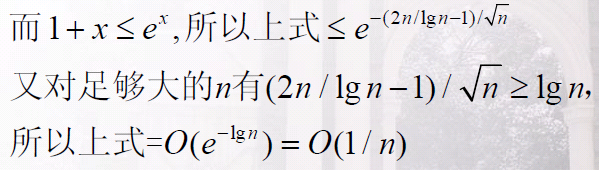
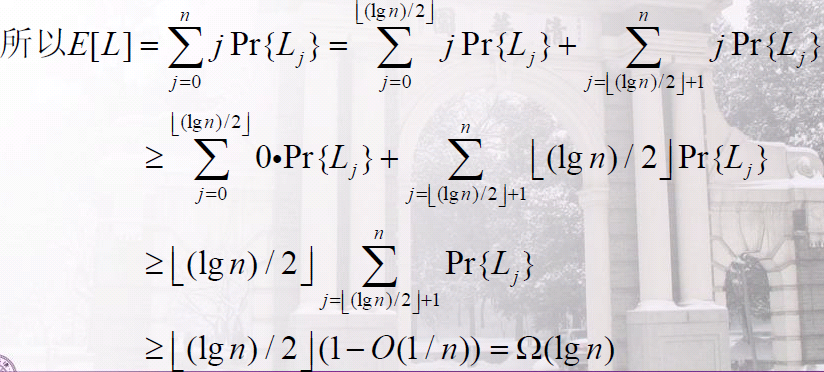
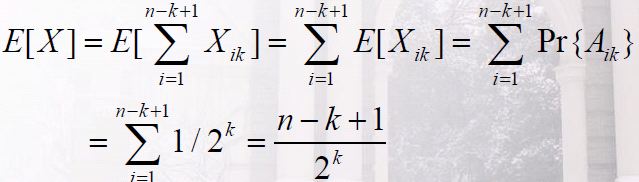
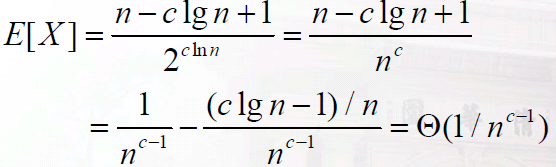
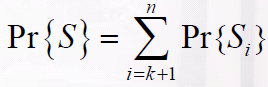

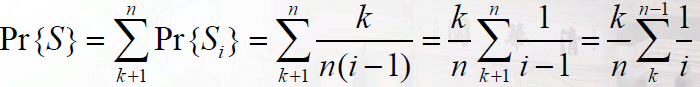
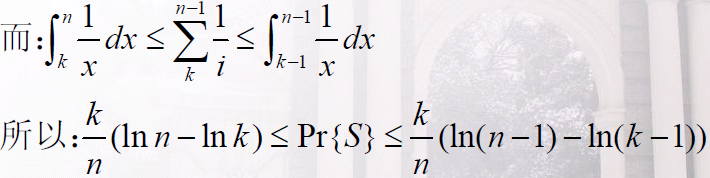













 911
911











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








