划分树基础 —— HDU 2665 Kth number

对应 HDU 题目 ：点击打开链接

Kth number

Time Limit: 15000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 7186    Accepted Submission(s): 2298

Problem Description

Give you a sequence and ask you the kth big number of a inteval.

 

Input

The first line is the number of the test cases. 
For each test case, the first line contain two integer n and m (n, m <= 100000), indicates the number of integers in the sequence and the number of the quaere. 
The second line contains n integers, describe the sequence. 
Each of following m lines contains three integers s, t, k. 
[s, t] indicates the interval and k indicates the kth big number in interval [s, t]

 

Output

For each test case, output m lines. Each line contains the kth big number.

 

Sample Input

  
  

   
   1 
10 1 
1 4 2 3 5 6 7 8 9 0 
1 3 2 
  
  

 

Sample Output

  
  

   
   2
  
  

 

题意：

      T组数据， 每组数据第一行有两个数 n，m。接下来一行有 n 个数， 接下来 m 行每行有3个数 l， r， k ，表示求区间[l，r] 内第 k 小的数。

思路：

      可以做为划分树的入门题：

      建树过程：

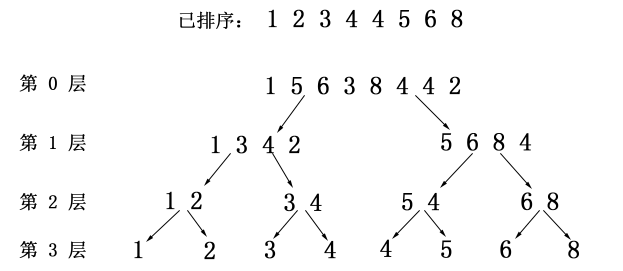
      先将原数组 a[] （数组下标从 1 开始）的副本 sort_a[] 升序排序，以第 0 层为例：

      mid = left + (right - left) / 2；然后按快速排序的思路对数组按原顺序进行划分，即比 sort_a[mid] 小的数放到下一层的左边；比 sort_a[mid] 大的数放到下一层的右边；与 sort_a[mid] 相等的数则根据下一层左边缺多少个数来进行填补。比如第 0 层 sort_a[mid] = 4；1，3，2 比 4 小， 放到下一层左边，而下一层左边长度为 mid - left + 1 = 4，所以要把一个 4 补到下一层左边；剩下的都放到右边。 下面各层递归处理。

      然而并没有这么简单，每一层还要维护一个 num[] 域，num[i] 表示区间 [left, i] 中被分配到下一层左边的数有多少个。比如对于第 0 层，num[5] = 2，因为区间 [1, 5] 中被分配到第 1 层左边的数有 2 个（1 和 3）

      查找过程：

      划分树一般为这样的结构体：

      typedef struct{

             type  a[N]; 

             type  num[N];

      }Layer;

      Layer  lay[M]；// M = 20 层可以满足 n = 2^20 的要求。 

      由此看出划分树的空间复杂度为 M * N，N 很大时可能相当不理想。 

      比如这个例子， 对于 ( l = 3，r = 7，k = 2 ) 这个请求，第 0 层的查询过程为：

      首先计算

      sum = lay[0].a[r] - lay[0].a[l-1] = 2 >= k = 2

      这里要注意如果 left == l，则 sum = lay[0].a[r]；

      所以下一层的查询应该在左边进行，可是下一层的查询区间怎样确定呢？

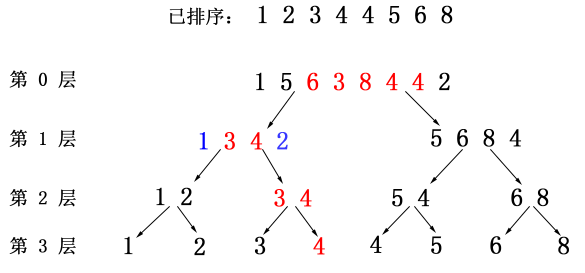
      可以知道，在不断往下的时候区间 [l，r] 是不断缩小的（下图红色部分）。第 1 层左边的蓝色的 1 是缩小的部分，右边的蓝色的 2 也是缩小的部分；仔细分析可以发现第 1 层左边缩小的个数是第 0 层的 num[l-1]；第一层右边缩小的个数是第 0 层的 num[right] - num[r-1]。

      左子树的起始下标为 left，右子树的起始下标为 mid + 1。

      因此如果 sum >= k 说明 [l，r] 区间的第 k 小的数在第一层的左边，进入第一层的左子树；而区间 [l, r] 应改为 [ left + num[l-1]，left + num[r] - 1 ]；

      而 sum < k 则进入第一层的右子树；而区间 [l, r] 应该为 [ mid + 1 + l - left - num[l-1]，mid + 1 + r - left - sum[r] ]

      划分树的基础部分大概就是这样，此题代码把输入改改可以解决 POJ 2104 和 POJ 2761。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define N 100010
int sort_a[N];

typedef struct{
    int a[N];
    int num[N];
}Layer;

Layer lay[25];

int cmp(void const *_a, void const *_b)
{
    int *a = (int *)_a;
    int *b = (int *)_b;
    return *a - *b;
}

void build(int left, int right, int cur)
{
    int i;
    int mid;
    int lson_p;
    int rson_p;
    int put_left;
    if(left == right) 
        return;
    mid = left + (right - left) / 2;
    put_left = mid - left + 1;
    for(i = left; i <= right; i++)
        if(lay[cur].a[i] < sort_a[mid])
            put_left--;
    lson_p = left;
    rson_p = mid + 1;
    for(i = left; i <= right; i++){
        if(i == left)
            lay[cur].num[i] = 0;
        else 
            lay[cur].num[i] = lay[cur].num[i-1];
        if(lay[cur].a[i] < sort_a[mid]){
            lay[cur].num[i]++;
            lay[cur+1].a[lson_p++] = lay[cur].a[i];
        }
        else if(lay[cur].a[i] == sort_a[mid]){
            if(put_left){
                put_left--;
                lay[cur].num[i]++;
                lay[cur+1].a[lson_p++] = lay[cur].a[i];
            }
            else
                lay[cur+1].a[rson_p++] = lay[cur].a[i];
        }
        else
            lay[cur+1].a[rson_p++] = lay[cur].a[i];
    }
    build(left, mid, cur + 1);
    build(mid + 1, right, cur + 1);
}

int Query(int left, int right, int cur, int l, int r, int k)
{
    int mid;
    int s;
    int ss;
    if(left == right)
        return lay[cur].a[left];
    mid = left + (right - left) / 2;
    if(left == l){
        s = 0;
        ss = lay[cur].num[r];
    }
    else{
        s = lay[cur].num[l-1];
        ss = lay[cur].num[r] - s;
    }
    if(ss >= k)
        return Query(left, mid, cur + 1, left + s, left + ss + s - 1, k);
    else 
        return Query(mid + 1, right, cur + 1, mid + 1 + l - left - s, mid + 1 + r - left - ss - s, k - ss);
}

int main()
{
#if 0
    freopen("in.txt","r",stdin);
#endif
    int T;
    scanf("%d", &T);
    while(T--){
        int n, m;
        scanf("%d%d", &n, &m);
        int i, j;
        for(i = 0; i < n; i++){
            scanf("%d", sort_a + i);
            lay[0].a[i] = sort_a[i];
        }
        qsort(sort_a, n, sizeof(int), cmp);
        build(0, n - 1, 0);
        for(i = 0; i < m; i++){
            int l, r, k;
            scanf("%d%d%d", &l, &r, &k);
            printf("%d\n", Query(0, n - 1, 0, l - 1, r - 1, k));
        }
    }
    return 0;
}