排序是计算机内经常进行的一种操作,其目的是将一组“无序”的记录序列调整为“有序”的记录序列,分内部排序和外部排序。若整个排序过程不需要访问外存便能完成,则称此类排序问题为内部排序。反之,若参加排序的记录数量很大,整个序列的排序过程不可能在内存中完成,则称此类排序问题为外部排序。
冒泡排序
对要排序的数据,从上到下依次比较两个相邻的数并加以调整,将最大的数向下移动,较小的数向上冒起。即:每一趟依次比较相邻的两个数据元素,将较小的数放在左边,循环进行同样的操作,直到全部待排序的数据元素排完。平均时间复杂度为o(n²)。
void bubbleSort(int *array,int length)
{
int i,j;
for(i=0;i<length;i++)
for(j=0;j<length-i-1;j++)
{
if(array[j]>array[j+1])
swap(&array[j],&array[j+1]);
}
}
void swap(int *a,int *b)
{
int temp=*a;
*a=*b;
*b=temp;
}
快速排序
快速排序是在实践中最快的已知排序算法,它的平均运行时间是O(NlogN),最坏情形是O(N^2)
设要排序的数组是A[0]……A[N-1],首先任意选取一个数据(通常选用数组的第一个数)作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序。然后再分别对前面后面的序列进行快速排序,值得注意的是,快速排序不是一种稳定的排序算法,也就是说,多个相同的值的相对位置也许会在算法结束时产生变动。
#define Cutoff (3)
//选用三数中值分割法选取枢纽元
int Median3(int array[],int left,int right)
{
int center = (left + right)/2 ;
if(array[left]>array[center])
Swap(&array[left],&array[center]);
if(array[left]>array[right])
Swap(&array[left],&array[right]);
if(array[center]>array[right])
Swap(&array[center],&array[right]);
//array[left]<=array[center]<=array[right]
Swap(&array[center],&array[right-1]);
return array[right-1];
}
void quickSort(int array[], int left,int right)
{
int i,j;
int pivot;
if (left + Cutoff <= right)
{
pivot = Median3(array,left,right);
i = left;
j = right-1;
for ( ; ; )
{
while(array[++i] < pivot){}
while(array[--j] > pivot){}
if( i< j )
Swap(&array[i],&array[j]);
else
break;
}
Swap(&array[i],&array[right-1]);
quickSort(array,left,i-1);
quickSort(array,i+1,right);
}
else
insertSort(array+left,right-left+1);
}
选择排序
将待排序序列分为两部分,一部分为有序序列,另一部分为无序序列。第一趟:从a[0]到a[n-1]中找到最小的数a[i],然后将a[i]与a[0]交换,第二趟:从a[1]到a[n-1]中找到最小的数a[j],然后将a[j]与a[1]交换,第三趟:从a[2]到a[n-1]中找到最小的数a[k],然后将a[k]与a[2]交换 ……
例如:
{13,15,37,89,60,39,12,109,56,72}
第一趟 :12 {15,37,89,60,39,13,109,56,72}
第二趟:12 ,13 {37,89,60,39,15,109,56,72}
第三趟:12 ,13 ,15 {89,60,39,37,109,56,72}
void selectSort(int *array,int length)
{
int i,j,min,minindex=0;
for(i=0;i<length-1;i++)
{
min=array[i];
minindex=i;
for(j=i+1;j<length;j++)
if(array[j]<min)
{
minindex=j;
min=array[j];
}
if(minindex!=i)
swap(&array[minindex],&array[i]);
for(int i=0;i<length;i++)
printf("%3d",array[i]);
printf("\n");
}
}堆排序
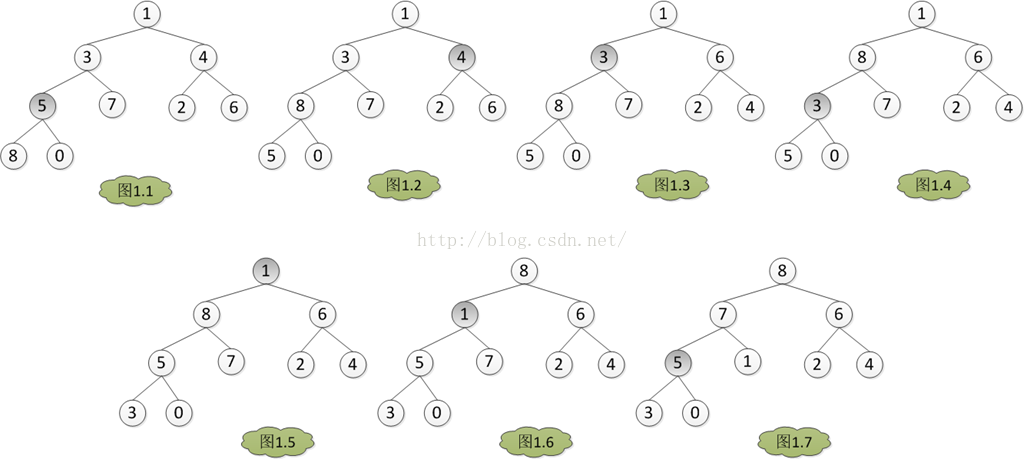
n个关键字序列Kl,K2,…,Kn称为(Heap),当且仅当该序列满足如下性质(简称为堆性质):(1)ki<=k(2i)且ki<=k(2i+1)(1≤i≤ n/2),当然,这是小根堆,大根堆则换成>=号。//k(i)相当于二叉树的非叶子结点,K(2i)则是左子节点,k(2i+1)是右子节点 .
堆是具有如下性质的二叉树:每个结点的值都大于或等于其左右孩子节点的值(称为大顶堆);或每个结点的值都小于或等于其左右孩子结点的值(称为小顶堆)。
堆排序:如果在输出堆顶的最小值之后,使得剩余n-1个元素序列重又建成一个堆,则得到n个元素中的次小值,如此反复执行,便能得到一个有序序列。
//第i个结点的左子结点为2*i+1
#define leftChild(i) (2*(i)+1)//调整第i到第n个元素使之成为大顶堆;
void perDown(int array[],int i,int n)
{
int child;
int tmp;
for( tmp = array[i];leftChild(i)<n;i=child)
{
child = leftChild(i);
if(child != n-1&&array[child+1]>array[child])//比较该结点的左右孩子结点,取最大值;
child++;
if(tmp<array[child])//将第i个节点的值置为最大;
array[i] = array[child];
else
break;
}
array[i] = tmp;
}
void HeapSort(int array[],int n)
{
void perDown(int array[],int i,int n);
int i;
for(i=n/2;i>=0;i--)
perDown(array,i,n);
for(i = n-1;i>0;i--)
{
// swap(&array[0],&array[i]);
int t = array[i];
<span style="white-space:pre"> </span>array[i] = array[0];
<span style="white-space:pre"> </span>array[0] = t;
perDown(array,0,i);
}
}直接插入排序
将一个记录插入到已排序好的有序表中,从而得到一个新的、记录数增1的有序表。(将第N个数插入到前面N-1个已经排列好的序列中时,先检索前N-1个数的序列,确定要插入的位置,然后直接插入)
例如
原有续表{1,2,5,8,10,15,20} 7
找出插入位置{1,2,5 ,8,10,15,20}7
新有序表{1,2,5,7,8,10,15,20}
void insertSort(int *array,int length)
{
int i,j,temp;
for(i=1;i<length;i++)
{
temp=array[i];
flag=i;
for(j=i-1;j>=0;j--)
{
if(temp<array[j])
{
array[j+1]=array[j];
flag=j;
}
}
array[flag]=temp;
printf("\n");
}
}最好情况下为o(n),最坏为o(n²),平均为o(n²),同样是o(n²)直接插入排序法比冒泡和选择排序要好。
希尔排序
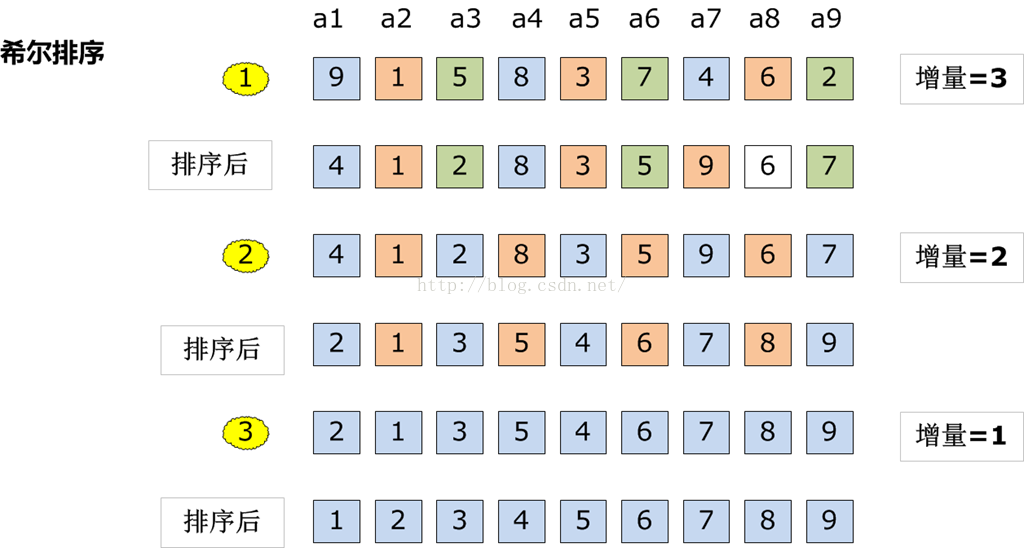
void shellSort(int *array,int length)
{
int i,j,increment,temp;
for(increment=length/2;increment>0;increment/=2)
for(i=increment;i<length;i++)
{
temp=array[i];
for(j=i;j>=increment;j-=increment)
if(temp<array[j-increment])
array[j]=array[j-increment];
else
break;
array[j]=temp;
}
}归并排序
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并过程为:比较a[i]和a[j]的大小,若a[i]≤a[j],则将第一个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1;否则将第二个有序表中的元素a[j]复制到r[k]中,并令j和k分别加上1,如此循环下去,直到其中一个有序表取完,然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现,先把待排序区间[s,t]以中点二分,接着把左边子区间排序,再把右边子区间排序,最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。
归并操作(merge),也叫归并算法,指的是将两个顺序序列合并成一个顺序序列的方法。
设有数列{6,202,100,301,38,8,1}
初始状态:6,202,100,301,38,8,1
第一次归并后:{6,202},{100,301},{8,38},{1},比较次数:3;
第二次归并后:{6,100,202,301},{1,8,38},比较次数:4;
第三次归并后:{1,6,8,38,100,202,301},比较次数:4;
总的比较次数为:3+4+4=11,;
逆序数为14;
void mergeSort(int array[],int n)
{
void Msort(int array[],int tmpArray[],int left,int right);
int *tmpArray;
tmpArray = (int*)malloc(n*sizeof(int));
if(tmpArray != NULL)
{
Msort(array,tmpArray,0,n-1);
free(tmpArray);
}
else
printf("NO SPACE FOR TMP ARRAAY!!");
}
void Msort(int array[],int tmpArray[],int left,int right)
{
void merge(int array[],int tmpArray[],int lops,int rops,int rightEnd);
int center;
if(left < right)
{
center = (left+right)/2 ;
Msort(array,tmpArray,left,center);
Msort(array,tmpArray,center+1,right);
merge(array,tmpArray,left,center+1,right);
}
}
//lops:start of the left half,rops:start of the right half
void merge(int array[],int tmpArray[],int lops,int rops,int rightEnd)
int i,leftEnd,numElements,tmpPos;
leftEnd = rops -1;
tmpPos = lops;
numElements = rightEnd - lops + 1;
while(lops<=leftEnd && rops<=rightEnd)
if(array[lops]<=array[rops])
tmpArray[tmpPos++] = array[lops++];
else
tmpArray[tmpPos++] = array[rops++];
while(lops<=leftEnd)
tmpArray[tmpPos++]=array[lops++];
while(rops<=rightEnd)
tmpArray[tmpPos++]=array[rops++];
for(i=0;i<numElements;i++,rightEnd--)
array[rightEnd] = tmpArray[rightEnd];
}






















 234
234











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








