神经网络之梯度下降与反向传播（下）

最新推荐文章于 2024-02-03 07:30:00 发布

2014wzy

最新推荐文章于 2024-02-03 07:30:00 发布

阅读量8.3k

点赞数 2

分类专栏：深度学习 Python

深度学习同时被 2 个专栏收录

43 篇文章 4 订阅

订阅专栏

Python

22 篇文章 1 订阅

订阅专栏

一、符号与表示

本文介绍全连接人工神经网络的训练算法——反向传播算法（关于人工神经网络可参考“卷积神经网络简介”第二节）。反向传播算法是一种有监督训练算法。它本质上是梯度下降法（参考“上篇”）。人工神经网络的参数多且“深”，梯度计算比较复杂。在人工神经网络模型提出几十年后才有研究者发明了反向传播算法来解决深层参数的训练问题。本文将详细讲解该算法的原理及实现。

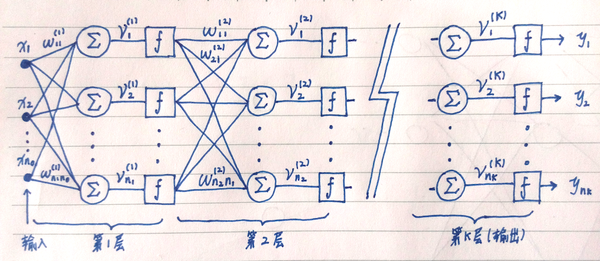
首先把文中用来表示神经网络的各种符号描述清楚。请看图 1.1 。

图 1.1

图 1.1 描绘了一个多层全连接神经网络。该网络共有 K 层。第 k 层包含 $n_k$ 个神经元。最后一层（第 K 层）是输出层。第 K 层的输出 $\textbf{y}=\left(y_1,y_2,\cdots,y_{n_K}\right)^T$ 是神经网络的输出向量（上标 T 表示向量／矩阵转置）。该神经网络接受 $n_0$ 个输入 $\textbf{x}=\left(x_1,x_2,\cdots,x_{n_0}\right)^T$ 。第 k 层（ k < K）是隐藏层，其第 j 个神经元以及它的前后连接如图 1.2 。

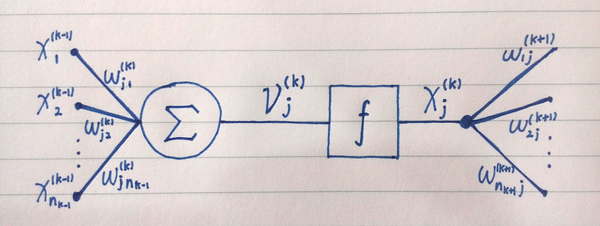
图 1.2

圆圈 $\Sigma$ 是线性加和单元。它连接到第 k-1 层的 $n_{k-1}$ 个神经元的输出 $x_s^{k-1} \left(1\leq s\leq n_{k-1}\right)$ 。 $w_{js}^{(k)}$ 是连接的权重。线性加和单元的计算结果 $v_{j}^{(k)}$ 称作该神经元的“激励水平”，由 [1.1] 计算得到。

$v_{j}^{(k)} = \sum_{s=1}^{n_{k-1}}{w_{js}^{(k)} x_{s}^{(k-1)}} =\left(w_{j1}^{(k)},w_{j2}^{(k)},\dots,w_{jn_{k-1}}^{(k)}\right)\left(\begin{array}{ccc}x_{1}^{(k-1)} \\ x_{2}^{(k-1)} \\ \vdots \\ x_{n_{k-1}}^{(k-1)} \end{array}\right) \quad\left[1.1\right]$

从 [1.1] 可看出，神经元的“激励水平”是其权值向量与输入向量的内积。f 是神经元的激励函数。激励函数的输入是激励水平，输出是神经元的输出：

$x_{j}^{(k)}=f(v_{j}^{(k)})\quad\left[1.2\right]$

$x_{j}^{(k)}$ 提供给下一层（第 k+1 层）的 $n_{k+1}$ 个神经元作为输入之一。例如 $x_{j}^{(k)}$ 乘上权重 $w_{sj}^{(k+1)}$ 送给第 k+1 层第 s 个神经元的线性加和单元。

神经网络的计算过程就是将输入向量提供给网络第 1 层各神经元，经过加权求和得到激励水平，之后对激励水平施加激励函数得到结果。将这些结果输送给下一层神经元。依此类推，直到最后一层（输出层）计算出结果，就是神经网络的输出向量。

二、训练过程

训练集中的样本形如： $\left[\textbf{x},\bar{\textbf{y}}\right]=\left[\left(x_{1},x_{2},\dots,x_{n_0}\right)^T, \ \left(\bar{y}_{1},\bar{y}_{2},\dots,\bar{y}_{n_K}\right)^T\right]$ 。输入包含 $n_0$ 个值，目标值包含 $n_K$ 个值，分别对应神经网络的输入／输出维度。训练这样进行：将训练集中的样本一个接一个提交给神经网络。神经网络对样本输入 $\textbf{x}$ 计算输出 $\textbf{y}$ ，然后计算样本目标值与输出的平方和误差：

$E=\frac{1}{2} \sum_{i=1}^{n_K}{\left(\bar{y}_{i}-y_{i}\right)^2}=\frac{1}{2}\left(\bar{\textbf{y}}-\textbf{y}\right)^T\left(\bar{\textbf{y}}-\textbf{y}\right)\quad\left[2.1\right]$

视输入 $\textbf{x}$ 为固定值，把 $E$ 当作全体权值 $W=\left\{w_{ji}^{(k)}\right\}$ 的函数。求 $E$ 的梯度 $\triangledown E$ ，然后用下式更新全体权值：

$W\left(s+1\right)=W\left(s\right)-\eta \triangledown E \quad\left[2.2\right]$

[2.2] 是梯度下降法的更新式。其中 $\eta$ 是步长，s 是迭代次数。梯度 $\triangledown E$ 向量由 $E$ 对每一个权重 $w_{ji}^{(k)}$ 的偏导数 $\frac{\partial E}{\partial w_{ji}^{(k)}}$ 构成。更新式 [2.2] 等价于对每一个权重进行更新：

$w_{ji}^{(k)}\left(s+1\right)=w_{ji}^{(k)}\left(s\right)-\eta\frac{\partial E}{\partial w_{ji}^{(k)}} \quad\left[2.3\right]$

对每一个提交给神经网络的样本用式 [2.3] 进行一次权值更新，直到对所有样本的平均 $E$ 值 MSE（ mean square error ）小于一个预设的小阈值，此时训练完成。

训练算法还可以有很多变体。例如动态步长、冲量等（参考“上篇”）。也可以将一批样本在同样的权值 $W$ 下计算 $\triangledown E$ ，然后根据这一批 $\triangledown E$ 的平均值更新 $W$ 。这称为批量更新。训练的关键问题是如何计算 $\triangledown E$ ，即如何计算每一个 $\frac{\partial E}{\partial w_{ji}^{(k)}}$ 。

三、反向传播

回顾图 1.1 和图 1.2 。首先对第 k 层第 j 个神经元关注这样一个值 $\delta_{j}^{(k)}$ 。定义：

$-\delta_{j}^{(k)}= \frac{\partial E}{\partial v_{j}^{(k)}} \quad\left[3.1\right]$

将 $\delta_{j}^{(k)}$ 定义为 $E$ 对第 k 层第 j 个神经元的激励水平 $v_{j}^{(k)}$ 的偏导数的相反数。根据求导链式法则，有：

$\frac{\partial E}{\partial w_{ji}^{(k)}} =\frac{\partial E}{\partial v_{j}^{(k)}} \ \frac{\partial v_j^{(k)}}{\partial w_{ji}^{(k)}} \quad\left[3.2\right]$

将 [3.2] 等号右侧的第二项展开：

$\frac{\partial v_j^{(k)}}{\partial w_{ji}^{(k)}} =\frac{\partial}{\partial w_{ji}^{(k)}} \left(\sum_{s=1}^{n_{k-1}}{w_{js}^{(k)} x_{s}^{(k-1)}} \right)=x_{i}^{(k-1)}\quad\left[3.3\right]$

结合定义 [3.1] ，有：

$\frac{\delta E}{\delta w_{ji}^{(k)}} =-\delta_{j}^{(k)}x_{i}^{(k-1)}\quad\left[3.4\right]$

可见有了 $\delta_{j}^{(k)}$ 就能计算 $E$ 对任一权重 $w_{ji}^{(k)}$ 的偏导数。接下来的问题就是如何计算 $\delta_{j}^{(k)}$ 。采用一种类似数学归纳法的方法。首先计算第 K 层（输出层）某个神经元 j 的 $\delta_{j}^{(K)}$ 。

$-\delta_{j}^{(K)}=\frac{\partial E}{\partial v_j^{(K)}} =\frac{\partial E}{\partial y_j}\frac{\partial y_j}{\partial v_j^{(K)}}=\frac{\partial E}{\partial y_j}f^{'} \left(v_j^{(K)}\right)=\frac{\partial}{\partial y_j} \left(\frac{1}{2} \sum_{s=1}^{n_K}{\left(\bar{y}_{s}-y_{s}\right)^2}\right)f^{'} \left(v_j^{(K)}\right)=-\left(\bar{y}_{j}-y_{j}\right)f^{'} \left(v_j^{(K)}\right)\quad\left[3.5\right]$

$f^{'}$ 表示 f 的导函数。[3.5] 展示了推导过程，其结论是：对于输出层（第 K 层）第 j 个神经元来说：

$\delta_{j}^{(K)}=\left(\bar{y}_{j}-y_{j}\right)f^{'} \left(v_j^{(K)}\right)\quad\left[3.6\right]$

$\delta_{j}^{(K)}$ 等于目标值 $\bar{y_j}$ 与输出 $y_j$ 之差乘上 f 在 $v_{j}^{(k)}$ 的偏导数。可以将 $\delta_{j}^{(K)}$ 看成一个经过缩放的误差。这个观点在后面讨论反向传播的意义以及传播的是到底什么时有用。

现在推导某个隐藏层——第 k 层第 j 个神经元的 $\delta_{j}^{(k)}$ 。将第 k+1 层的全体 $v_{j}^{(k+1)}$ 值视作一个向量：

$\textbf{v}^{k+1}=\left(v_1^{k+1},v_2^{k+1},\cdots,v_{n_{k+1}}^{k+1}\right)^T\quad\left[3.7\right]$

再次回顾图 1.1 和图 1.2 。 $v_{j}^{(k)}$ 被施加激励函数 f 得到 $x_{j}^{(k)}$ 。 $x_{j}^{(k)}$ 乘上第 k+1 层各神经元对该输出的各权值，再与第 k 层其他神经元的输出（加权后）相加，得到第 k+1 层各神经元的激励水平 $\textbf{v}^{k+1}$ 。 $\textbf{v}^{k+1}$ 经过后面的网络得到最终输出，最终计算出 $E$ 。将整个过程视作一个三阶段的复合函数，连续使用链式法则，有：

$-\delta_j^{(k)}=\frac{\partial E}{\partial v_j^{(k)}}=\frac{\partial E}{\partial \textbf{v}^{(k+1)}} \ \frac{\partial \textbf{v}^{(k+1)}}{\partial x_j^{(k)}} \ \frac{\partial x_j^{{k}}}{\partial v_j^{(k)}}\quad\left[3.8\right]$

等号右侧第一项是对一个 $R^{n_{k+1}}\rightarrow R^1$ 函数求导。它是 $1\times n_{k+1}$ 元向量。它的第 i 个元素是：

$\frac{\partial E}{\partial v_{i}^{(k+1)}} =-\delta _{i}^{(k+1)}\quad\left[3.9\right]$

第项是对一个 $R^1\rightarrow R^{n_{k+1}}$ 函数求导。它是 $n_{k+1}\times 1$ 元向量。它的第 i 个元素为：

$\frac{\partial v_i^{(k+1)}}{\partial x_j^{(k)}}=\frac{\partial}{x_j^{(k)}}\left(\sum_{s=1}^{n_k}{w_{is}^{(k+1)}} x_s^{(k)}\right)=w_{ij}^{(k+1)}\quad\left[3.10\right]$

最后一项是激励函数 f 在 $v_{j}^{(k)}$ 的偏导数。结合 [3.8]、[3.9] 和 [3.10] 得到：

$-\delta_j^{(k)}=\frac{\partial E}{\partial v_j^{(k)}}=\left(-\delta _{1}^{(k+1)},-\delta _{2}^{(k+1)},\cdots,-\delta _{n_{k+1}}^{(k+1)}\right)\left(\begin{array}{ccc}w_{1j}^{(k+1)}\\w_{2j}^{(k+1)}\\\vdots\\w_{n_{k+1}j}^{(k+1)}\end{array}\right) f^{'}(v_j^{(k)})=-\left(\sum_{s=1}^{n_{k+1}}{\delta _{s}^{(k+1)}w_{sj}^{(k+1)}}\right)f^{'}(v_j^{(k)})\quad\left[3.11\right]$

[3.11] 是推导过程，它的结论是：

$\delta_{j}^{(k)}=\left(\sum_{s=1}^{n_{k+1}}{\delta _{s}^{(k+1)}w_{sj}^{(k+1)}}\right)f^{'}(v_j^{(k)})\quad\left[3.12\right]$

注意 [3.8] 至 [3.10] 的推导过程运用了多元函数的求导链式法则。一个 $R^n\rightarrow R^m$ 函数的导数是一个 $m\times n$ 的矩阵。多元复合函数的求导链式法则是将导矩阵相乘。具体证明请可参考书目 [1] 附录部分或其他微积分教材。至此所有要素齐备。综合 [2.3]、 [3.4]、[3.6] 和 [3.12] 可得反向传播算法权值更新规则如下：

$\begin{equation} \left\{ \begin{aligned} w_{ji}^{(k)}\left(s+1\right)=w_{ji}^{(k)}\left(s\right)-\eta\frac{\delta E}{\delta w_{ji}^{(k)}} =w_{ji}^{(k)}\left(s\right)+\eta\delta_{j}^{(k)}x_{i}^{(k-1)}\\\delta_{j}^{(K)}=\left(\bar{y}_{j}-y_{j}\right)f^{'} \left(v_j^{(K)}\right)\\\delta_{j}^{(k)}=\left(\sum_{s=1}^{n_{k+1}}{\delta _{s}^{(k+1)}w_{sj}^{(k+1)}}\right)f^{'}(v_j^{(k)}), \ k<K \end{aligned} \right. \end{equation} \quad[3.13]$

用更紧凑的矩阵形式表示反向传播算法。由 [3.11] 可以得到：

$\Delta^{(k)}=\left(\delta _{1}^{(k)},\delta _{2}^{(k)},\cdots,\delta _{n_{k}}^{(k)}\right)=\left(-\frac{\partial E}{\partial v_1^{(k)}},-\frac{\partial E}{\partial v_2^{(k)}},\cdots,-\frac{\partial E}{\partial v_{n_{k}}^{(k)}}\right)\\=\left(\delta _{1}^{(k+1)},\delta _{2}^{(k+1)},\cdots,\delta _{n_{k+1}}^{(k+1)}\right)\left(\begin{array}{ccc}w_{11}^{(k+1)}\\w_{21}^{(k+1)}\\\vdots\\w_{n_{k+1}1}^{(k+1)}\end{array}\begin{array}{ccc}w_{12}^{(k+1)}\\w_{22}^{(k+1)}\\\vdots\\w_{n_{k+1}2}^{(k+1)}\end{array}\begin{array}{ccc}\cdots\\\cdots\\\ddots\\\cdots\end{array}\begin{array}{ccc}w_{1n_{k}}^{(k+1)}\\w_{2n_{k}}^{(k+1)}\\\vdots\\w_{n_{k+1}n_{k}}^{(k+1)}\end{array}\right) \left(\begin{array}{ccc}f^{'}(v_1^{(k)})\\0\\\vdots\\0\end{array}\begin{array}{ccc}0\\f^{'}(v_2^{(k)})\\\vdots\\0\end{array}\begin{array}{ccc}\cdots\\\cdots\\\ddots\\\cdots\end{array}\begin{array}{ccc}0\\0\\\vdots\\f^{'}(v_{n_k}^{(k)})\end{array}\right)\\=\Delta^{(k+1)}W^{(k+1)}F^{(k)}$

[3.14]

如 [3.14] 所示，第 k 层全体 $\delta_{j}^{(k)}$ 值组成的向量 $\Delta^{(k)}$ 可由本层的激励函数导数对角阵 $F^{(k)}$ ，第 k+1 层的 $\Delta^{(k+1)}$ 和权值矩阵 $W^{(k+1)}$ 计算得到。输出层（第 K 层）的 $\Delta^{(K)}$ 这么计算：

$\Delta^{(K)}=\left(\bar{y}_{1}-y_{1},\bar{y}_{2}-y_{2},\cdots,\bar{y}_{n_K}-y_{n_K}\right)\left(\begin{array}{ccc}f^{'}(v_1^{(K)})\\0\\\vdots\\0\end{array}\begin{array}{ccc}0\\f^{'}(v_2^{(K)})\\\vdots\\0\end{array}\begin{array}{ccc}\cdots\\\cdots\\\ddots\\\cdots\end{array}\begin{array}{ccc}0\\0\\\vdots\\f^{'}(v_{n_k}^{(K)})\end{array}\right)=\left(\bar{\textbf{y}}-\textbf{y}\right)^TF^{(K)}\quad[3.15]$

[3.14] 和 [3.15] 就构成了反向传播计算。至于权值更新，对第 k 层的权值矩阵 $W^{(k)}$ 按 [3.16] 更新。其中 $X^{(k)}$ 是第 k 层输出（列）向量：

$W^{(k)}\left(s+1\right)=W^{(k)}\left(s\right)+\eta\Delta^{(k)^T}X^{(k)}\quad[3.16]$

综上所述，隐藏层 $\Delta^{(k)}$ 的计算利用了下一层的 $\Delta^{(k+1)}$ 。一个训练样本 $\textbf{x}$ “正向”通过网络计算输出 $\textbf{y}$ 。之后“反向”逐层计算 $\Delta^{(k)}$ 更新权值，并将 $\Delta^{(k)}$ 向前一层传播。所谓“反向”传播就是 $\Delta^{(k)}$ 的传播。以上推导没有包括神经元的偏置。把偏置看成一个连接到常量 1 的连接上的权值即可。

从计算式来看 $\delta_{j}^{(k)}$ 是 $E$ 对第 k 层第 j 个神经元的激励水平 $v_{j}^{(k)}$ 的偏导数的相反数。还存在另一个视角。上文已经谈到，输出层的 $\delta_{j}^{(K)}$ 是经过缩放的误差。隐藏层的 $\delta_{j}^{(k)}$ 以连接权值加权组合了下一层各神经元的 $\delta_{j}^{(k+1)}$ 。可以把 $\delta_{j}^{(k)}$ 定义为某种“局部误差”。于是反向传播算法就是反向传播局部误差——把总误差分摊到各个神经元头上，让它们调整自己。反向传播本质是梯度下降，而局部误差视角为理解算法提供了一种洞见。

四、实现

笔者用 python 实现了一个全连接神经网络。我们尝试拟合正弦函数：

$y=(sin(x)+1.0)/2.0 \quad [4.1]$

正弦函数经过了平移和缩放。构造一个单输入／单输出的 8x8x1 神经网络。两个隐藏层各有 8 个神经元，输出层有 1 个神经元。各层的激励函数都选用 sigmoid 函数：

$\frac{1}{1+e^{-x}} \quad [4.2]$

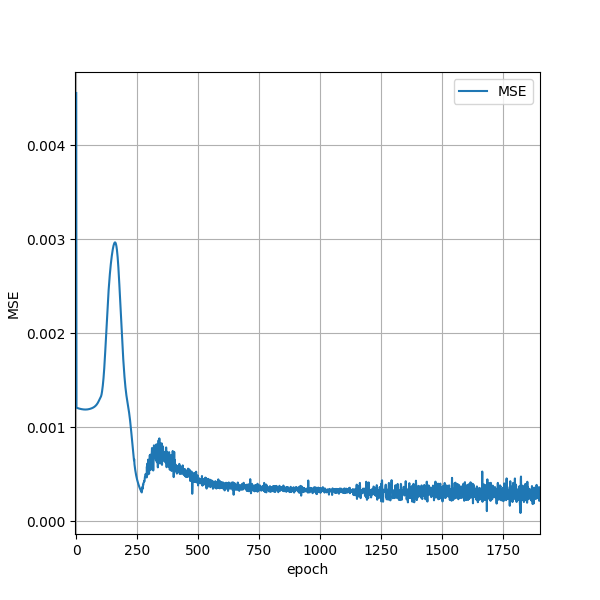
从 0.0 至 $2\pi$ 之间以 0.01 为间隔取样得到训练集。轮流将样本提交给神经网络进行权值更新。步长固定为 0.7 。当全部训练样本依次提交完一遍称为一个 epoch 。一个 epoch 接着一个 epoch 反复进行训练。神经网络对所有样本的 $E$ 的平均值是 MSE（ mean square error ）。限制最大迭代次数为 150,000 。当 MSE 小于阈值 1e-6 或训练达到最大迭代次数时终止训练，这称为一个 batch 。共进行 8 个 batch 。注意文中出现的 epoch 和 batch 都是按照作者个人在此的使用方式。文中 MSE 也并非标准的 MSE 。这几个术语与公认的定义有区别，在此是为了描述这个简单实现的样例神经网络程序。图 4.1 是 MSE 随着训练 epoch 数量变化的情况。

图 4.1

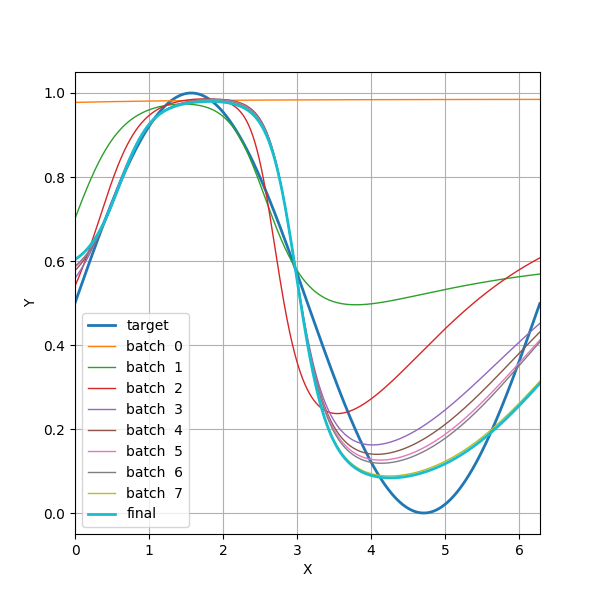
图 4.2 展示了目标正弦曲线。训练开始前（ batch 0 ）、每个 batch 结束时（ batch 1~7 ）、以及整个训练结束后（ final ）神经网络的输出曲线。可见我们的神经网络近似拟合了正弦函数（艰难地拗成了 S 形曲线）。

图 4.2

最后附上代码。test.py 为测试代码。NN.py 为神经网络代码。

test.py

from NN import *
import matplotlib.pyplot as plt

# 创建一个 6x6x1 的神经网络。
network = Network()
network.add_layer(Layer(number_of_neurons=8, input_size=1))
network.add_layer(Layer(number_of_neurons=8))
network.add_layer(Layer(number_of_neurons=1))

# 构造训练数据集：经平移和缩放的正弦曲线。
x = np.arange(0, 2 * np.pi, 0.01)
x = x.reshape((len(x), 1))
y = (np.sin(x) + 1.0) / 2.0

# 绘图。
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)

# 绘制目标曲线。
yt = np.array(y).ravel()
xs = np.array(x).ravel()
ax.plot(xs, yt, label="target", linewidth=2.0)

# 进行 10 个 batch
for i in np.arange(0, 8):
    # 绘制当前网络输出曲线。
    yp = network.predict(x).ravel()
    ax.plot(xs, yp, label="batch {:2d}".format(i))

    print("==================== Batch {:3d} ====================".format(i + 1))

    # 输入 x 为二维数组，形状为 (样本数, 输入向量维度) 。
    # 标准值 y 也是二维数组，形状为 (样本数, 输出向量维度) 。
    network.train(x=x, y=y, eta=0.7, threshold=1e-6, max_iters=150000)

# 训练完成后绘制网络输出曲线。
yp = network.predict(x).ravel()
ax.plot(xs, yp, label="final", linewidth=2.0)


# 目标和输出曲线图。
ax.grid()
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_xlim([0, 2 * np.pi])
ax.legend()
plt.savefig("target.png")
plt.clf()
plt.cla()

# MSE 下降图。
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
ax.plot(network.error_history, label="MSE", linewidth=1.5)
ax.legend()
ax.grid()
ax.set_xlabel("epoch")
ax.set_ylabel("MSE")
ax.set_xlim([-5, len(network.error_history) - 1])
plt.savefig("error.png")
plt.clf()
plt.cla()

NN.py

import numpy as np


class Network:
    def __init__(self):
        self.layers = []
        self.error_history = []

    def add_layer(self, layer):
        if len(self.layers) > 0:
            layer.connect(self.layers[-1])
        else:
            layer.connect()

        self.layers.append(layer)

    def compute(self, x):
        result = np.array(x)
        for layer in self.layers:
            result = layer.compute(result)
        return result

    def predict(self, x):
        result = []
        for xx in x:
            result.append(self.compute(xx))
        return np.array(result)

    def train(self, x, y, eta=0.01, threshold=1e-3, max_iters=None):

        x = np.array(x)
        y = np.array(y)
        train_set_size = len(x)
        index = 0
        count = 0
        error = [100.0] * train_set_size
        batch = 1
        while True:

            input = x[index]
            label = y[index]
            output = self.compute(input)

            d = label - output

            index = (index + 1) % len(x)
            count += 1
            error[index] = 0.5 * np.dot(d, d)
            mean_error = np.mean(error)
            if count % train_set_size == 0:
                self.error_history.append(mean_error)
                print("Training. Batch {:6d}. MSE={:f}".format(batch, mean_error))
                batch += 1

            if mean_error <= threshold or (max_iters is not None and count > max_iters):
                break

            self.back_propagation(d)
            self.update(eta)

    def back_propagation(self, d):
        for layer in self.layers[::-1]:
            layer.back_propagation(d)

    def update(self, eta):
        for layer in self.layers:
            layer.update(eta)


class Layer:
    def __init__(self, number_of_neurons=10, input_size=5, activation="sigmoid"):
        self.number_of_neurons = number_of_neurons
        self.activation = activation
        self.neurons = []
        self.input_size = input_size
        self.next_layer = None

    def set_next_layer(self, layer):
        self.next_layer = layer

    def connect(self, last_layer=None):

        if last_layer is not None:
            self.input_size = last_layer.get_output_size()
            last_layer.set_next_layer(self)

        for i in np.arange(0, self.number_of_neurons):
            self.neurons.append(Neuron(self, i, self.activation))

    def get_output_size(self):
        return len(self.neurons)

    def compute(self, x):
        output = []
        for neuron in self.neurons:
            output.append(neuron.compute(x))
        return output

    def back_propagation(self, d):
        for neuron in self.neurons:
            neuron.back_propagation(d)

    def update(self, eta):
        for neuron in self.neurons:
            neuron.update(eta)


class Neuron:
    def __init__(self, layer, no, activation="sigmoid"):
        self.no = no
        self.layer = layer
        self.weights = np.array(np.random.rand(self.layer.input_size))
        self.activation = activation
        self.delta = 0.0
        self.activation_level = 0.0
        self.input = None

    @staticmethod
    def sigmoid(x):
        return 1.0 / (1.0 + np.power(np.e, -x))

    @staticmethod
    def sigmoid_grad(x):
        return np.power(np.e, -x) / np.power(1 + np.power(np.e, -x), 2)

    def compute(self, x):
        self.input = x
        self.activation_level = np.dot(self.input, self.weights)
        if self.activation == "sigmoid":
            return Neuron.sigmoid(self.activation_level)
        else:
            return self.activation_level

    def back_propagation(self, d):
        if self.layer.next_layer is not None:
            tmp = 0.0
            for neuron in self.layer.next_layer.neurons:
                tmp += neuron.delta * neuron.weights[self.no]
        else:
            tmp = d[self.no]

        if self.activation == "sigmoid":
            self.delta = tmp * Neuron.sigmoid_grad(self.activation_level)
        else:
            self.delta = tmp

    def update(self, eta):
        self.weights += eta * self.delta * np.array(self.input)

五、参考书目

［1］《最优化导论》（美）Edwin K. P. Chong（美） Stanislaw H. Zak

［2］《神经网络设计》（美）Martin T. Hagan（美）Howard B. Demuth（美）Mark Beale

［3］《机器学习》（美）Tom Mitchell

［4］《神经计算原理》（美）Fredric M. Han（美）Ivica Kostanic

2014wzy

关注

2
点赞
踩
21

收藏

觉得还不错? 一键收藏
2
评论
神经网络之梯度下降与反向传播（下）

一、符号与表示本文介绍全连接人工神经网络的训练算法——反向传播算法（关于人工神经网络可参考“卷积神经网络简介”第二节）。反向传播算法是一种有监督训练算法。它本质上是梯度下降法（参考“上篇”）。人工神经网络的参数多且“深”，梯度计算比较复杂。在人工神经网络模型提出几十年后才有研究者发明了反向传播算法来解决深层参数的训练问题。本文将详细讲解该算法的原理及实现。首先把文中用来表示神经网络
复制链接

扫一扫