常用排序算法总结2一一选择排序

定义

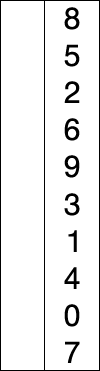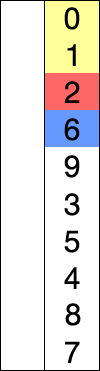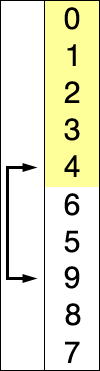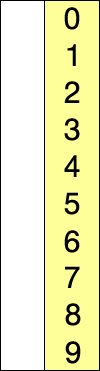
选择排序（英语：Selection sort）是一种简单直观的排序算法。它首先在未排序的序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。

算法步骤

选择排序算法的运作如下：

• 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
• 然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
• 以此类推，直到所有元素均排序完毕。

伪代码如下：

selection_sort(array, length)
{
    var i, j, min, temp;
    for (i = 0; i < length - 1; i++) {
        // 记录当前最小元素的位置
        min = i;
        for (j = i + 1; j < length; j++)
            if (array[min] > array[j])
                min = j;
        temp = array[min];
        array[min] = array[i];
        array[i] = temp;
    }
}

代码实现（java）

一般实现

/**
 *
 * Description: 选择排序的简单实现
 * <p>
 *
 * @param: @param nums
 * @return: void
 */
public static void selectionSort(int[] nums)
{
    int temp;
    for (int currentPlace = 0; currentPlace < nums.length - 1; currentPlace++) {
        int smallest = nums[currentPlace + 1];
        int smallestAt = currentPlace + 1;
        for (int check = currentPlace; check < nums.length; check++) {
            if (nums[check] < smallest) {
                smallestAt = check;
                smallest = nums[check];
            }
        }
        temp = nums[currentPlace];
        nums[currentPlace] = nums[smallestAt];
        nums[smallestAt] = temp;
    }
}

通用实现

/**
 *
 * Title: selectionSort
 * <p>
 * Description: 选择排序的简单实现（支持泛型）
 * <p>
 *
 * @param: @param comparable
 * @return: void
 * @throws
 */
public static <E extends Comparable<? super E>> void selectionSort(
            E[] comparable)
{
    E temp;
    for (int currentPlace = 0; currentPlace < comparable.length - 1; currentPlace++) {
        E smallest = comparable[currentPlace + 1];
        int smallestAt = currentPlace + 1;
        for (int check = currentPlace; check < comparable.length; check++) {
            if (comparable[check].compareTo(smallest) < 0) {
                smallestAt = check;
                smallest = comparable[check];
            }
        }
        temp = comparable[currentPlace];
        comparable[currentPlace] = comparable[smallestAt];
        comparable[smallestAt] = temp;
    }
}

算法复杂度分析

• 选择排序的交换操作介于0和(n-1)次之间。选择排序的比较操作为n(n-1)/2次之间。选择排序的赋值操作介于0和3(n-1)次之间。
• 比较次数O(n^2)，比较次数与关键字的初始状态无关，总的比较次数N=(n-1)+(n-2)+…+1=n(n-1)/2。交换次数O(n)，最好情况是，已经有序，交换0次；最坏情况是，逆序，交换n-1次。交换次数比冒泡排序较少，由于交换所需CPU时间比比较所需的CPU时间多，值较小时，选择排序比冒泡排序快。
• 原地操作几乎是选择排序的唯一优点，当空间复杂度（space complexity）要求较高时，可以考虑选择排序；实际适用的场合非常罕见。

参考文章

• 选择排序