在数学领域里,多项式是由变量以及标量(一般是实数或复数)经乘法及加法构法而成,属于整式的代数式。下列四种都是多项式: 多项式中每一个 x n 皆称之为多项式的项 次数:多项式 x n 中每一项的n为此项的次数 同次项:若有多个多项式,其中每一项的 x k 项称之为同次项 首项:指多项式的项中次数最大者,若多项式首项为n,则称此多项式为n次多项式
非多项式的例子:
这些式子的变量位在分母,称作分式,并非多项式。
 及
及  也是多项式,但若然
也是多项式,但若然 及
及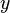 是可置换的变量,即
是可置换的变量,即 ,则这两个多项式是相同的。
,则这两个多项式是相同的。
单项式是指可以纯粹由乘法构法的多项式,如:  、
、 及
及  。单项式其实是不含加法或减法运算的整式.
。单项式其实是不含加法或减法运算的整式.
(注:有说单项式不是多项式,而多项式是由起码两个或以上的单项式相加起来而成。这是最常见单项式及多项式的定义。但多项式相加也可以是单项式,如 ,这个区分令理论研究变得复杂。若然把单项式也归纳为多项式,则多项式相加的和也是多项式,情况比较简单。)
,这个区分令理论研究变得复杂。若然把单项式也归纳为多项式,则多项式相加的和也是多项式,情况比较简单。)
几何学中,多项式是最简单的平滑曲线。简单是指它仅由乘法及加法构法;平滑皆因它类同口语中的平滑——以数学述语来说,它是无限可微,即可以对它的所有高次微分都存在。事实上,多项式的微分也是多项式。
简单及平滑的特点,使它在数值分析,图论,以及电脑绘图等,都发挥极大的作用。
历史
多项式的研究,源于“代数方程求解”, 是最古老数学问题之一。有些代数方程,如x+1=0,在负数被接受前,被认为是无解的。另一些多项式,如f(x)=x² + 1,是没有任何根的——严格来说,是没有任何实数根。若我们容许复数,则实数多项式或复数多项式都是有根的,这就是代数基本定理。
能否用根式求解的方法,表达出多项式的根,曾经是文艺复兴后欧洲数学主要课题。一元二次多项式的根相对容易。三次多项式的根需要引入复数来表示,即使是实数多项式的实数根。四次多项式的情况也是如此。经过多年,数学家仍找不到用根式求解五次多项式的一般方法,终于在1824年阿贝尔证明了这种一般的解法不存在,震掝数坛。数年后,伽罗华引入了群的概念,证明不存在用根式求解五次或以上的多项式的一般方法,其理论被引申为伽罗瓦理论。伽罗瓦理论也证明了古希腊难题三等分角不可能。另一个难题化圆为方的不可能证明,亦与多项式有关,证明的中心是圆周率乃一个超越数,即它不是有理数多项式的根。
正式定义
给一个环 R(可以是实数环,复数环或其他)及一个变量 x,则多项式是以下代数式:
-
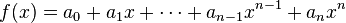 ,
,
当中 a0, …, an 是 R 的元素。用 Σ表达法,有
容易证明,多项式的和或积都是多项式,即多项式组成一个环 R[x],称为 R 上的(一元)多项式环。(注:在最一般的定义,a2x、xa2 及 axa 可以当作是不同的多项式,是不可置换环的例子。)
对于多变量多项式,我们可以类似方式定义。一个有 n 个变量的多项式,称为 n元多项式。通常以 R[x,y,z] 表示 R 为系数环,x,y 及 z 为变量的多项式环。
在 ![R[x_1,\ldots,x_n]](http://upload.wikimedia.org/math/7/f/8/7f8856b9fc884b3410dd6041b6c0d913.png) 中,
中, 称为单项式,其中 a∈ R是系数而
称为单项式,其中 a∈ R是系数而 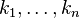 为非负整数,是
为非负整数,是 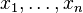 的次数。
的次数。 是这个单项式的次数。
是这个单项式的次数。
多项式的项数
若多项式以最少的单项式之和呈现,则每一个单项式都被称为此多项式的项,而项的数目称为项数。
例如多项式  的项数是四,故称为四项式。当中的
的项数是四,故称为四项式。当中的  、
、 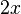 、
、 、
、  、都是此多项式的项。
、都是此多项式的项。
以上例子中的多项式可以写成四个以上单项式的和,如  是五个单项式的和。是以必须强调最少的单项式之和 。
是五个单项式的和。是以必须强调最少的单项式之和 。
另外的例子是  共有二项,此多项式称二项式。
共有二项,此多项式称二项式。
(注:若把  看作成在 R[c][x,y]=(R[c])[x,y] 中的多项式,则它只是三项式,分别是
看作成在 R[c][x,y]=(R[c])[x,y] 中的多项式,则它只是三项式,分别是  、
、 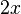 、及
、及  。 )
。 )
若是未知数X、Y、Z等若出现在分母里、根号里或是绝对值中,就不能定义为“多项式”。例如:
 ,因为出现在分母里,所以不是多项式。
,因为出现在分母里,所以不是多项式。 ,因为出现在根号里,所以不是多项式。
,因为出现在根号里,所以不是多项式。 ,因为出现在绝对值里,所以不是多项式。
,因为出现在绝对值里,所以不是多项式。
变项与常数项
多项式中含有变量的项称为变项,祇有数字的项称为常数项。 例如多项式: 中的
中的  、
、 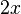 、
、  、 都是此多项式的变项。而
、 都是此多项式的变项。而 是常数项。
是常数项。
(注:若把  看作成在 R[c][x,y]=(R[c])[x,y] 中的多项式,则
看作成在 R[c][x,y]=(R[c])[x,y] 中的多项式,则  才是常数项。 )
才是常数项。 )
多项式的“元”
多项式中的变量种类称为元,各种变量以各字母表达(注:通常是x、y、z),一个多项式有n种变量就称为n元多项式。
例如: 中有
中有 、
、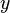 二元,是二元多项式。因有四项,可称二元四项式。
二元,是二元多项式。因有四项,可称二元四项式。
多项式的次数
多项式中次数最高的项的次数,即此多项式的次数。
例如多项式: 中
中  的次数最高,有三次方,故此多项式的次数为三。 因而此多项式可称为三元三次四项式。
的次数最高,有三次方,故此多项式的次数为三。 因而此多项式可称为三元三次四项式。 称为三次项,
称为三次项,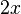 及
及  称为一次项或线性项,而 5 是 0 次项或常数项。
称为一次项或线性项,而 5 是 0 次项或常数项。
又例如多项式 ,
,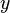 与
与  二项都是一次方,而常数项
二项都是一次方,而常数项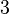 是零次方。故此多项式的次数为一。而此多项式项数为三,可称为一次三项式。
是零次方。故此多项式的次数为一。而此多项式项数为三,可称为一次三项式。
常数项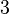 是零次方因为可被视为是
是零次方因为可被视为是  。而任何非零数字零次方都是1,故
。而任何非零数字零次方都是1,故 ,常数项的次数都为0。
,常数项的次数都为0。
又例如  的首项是五次,次项是四次,所以是个三元五次多项式。(注:若把
的首项是五次,次项是四次,所以是个三元五次多项式。(注:若把  看作成在 R[c][x,y]=(R[c])[x,y] 中的多项式,则第一项是三次而系数为 c2 ,第二项是四次,是个二元四次多项式。 )
看作成在 R[c][x,y]=(R[c])[x,y] 中的多项式,则第一项是三次而系数为 c2 ,第二项是四次,是个二元四次多项式。 )
多项式 p 的次数,记作 deg(p),由英语 degree 而来。 ,所以0这一多项式不计次数,故称为零多项式。常数多项式分为零次多项式和零多项式。所谓零次多项式是指每一个项(常数项除外)的系数都是0,而零多项式则指每一项的系数(包括常数项)都是0。1 次多项式又称为 线性多项式。多项式中的一次项又称为线性项。
,所以0这一多项式不计次数,故称为零多项式。常数多项式分为零次多项式和零多项式。所谓零次多项式是指每一个项(常数项除外)的系数都是0,而零多项式则指每一项的系数(包括常数项)都是0。1 次多项式又称为 线性多项式。多项式中的一次项又称为线性项。
多项式的升幂及降幂排列
多项式可依各单项式元的次数排列。
次数从低到高是升幂排列。 例如:以下多项式,从 排到
排到
次数从高到低是降幂排列。 例如:以下多项式,从 排到
排到
若一多项式为多元多项式,可依照其中一元排列。
例如: 是依X的次数排列。
是依X的次数排列。
亦可以y的次数排列。
例如:
一元多项式
一元多项式中次数最高的项,称为首项,其系数称为该多项式的首项系数。如  的首项系数为 3。首项系数为 1 的多项式称为首一多项式,如
的首项系数为 3。首项系数为 1 的多项式称为首一多项式,如  。
。
因式分解
把一多项式分成几个整式的积,称为因式分解。这些整式可称因式。
以下是常用的因式分解公式
多项式的运算
多项式乘法
把两个多项式相乘时,第一个多项式的每一个项都要与第二个多项式的每一个项相乘。例如:
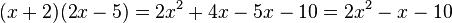
也可以利用矩阵乘法来进行:

多项式除法
多项式的除法与整数的除法类似。
(1)把被除式、除式按某个字母作降幂排列,并把所缺的项用零补齐.
(2)用被除式的第一项去除除式的第一项,得商式的第一项.
(3)用商式的第一项去乘除式,把积写在被除式下面(同类项对齐),消去相等项,把不相等的项结合起来.
(4)把减得的差当作新的被除式,再按照上面的方法继续演算,直到余式为零或余式的次数低于除式的次数时为止.被除式=除式×商式+余式
如果一个多项式除以另一个多项式,余式为零,就说这个多项式能被另一个多项式整除
例如,计算 。
。
因此,商是 ,余式是
,余式是 。 缺项补0
。 缺项补0
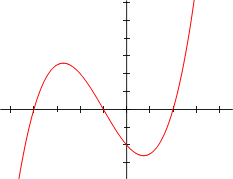
多项式座标图例子
一些低次数的多项式座标图:
|
|
|
|
|
|
多项式函数及多项式的根
给出多项式 f∈R[x1,...,xn] 以及一个 R-代数 A。对 (a1...an)∈An,我们把 f 中的 xj 都换成 aj,得出一个 A 中的元素,记作 f(a1...an)。如此,f 可看作一个由 An 到 A 的函数。
若然 f(a1...an)=0,则 (a1...an) 称作 f 的根或零点。
例如 f=x2+1。若然考虑 x 是实数、复数、或矩阵,则 f 会无根、有两个根、及有无限个根!
例如 f=x-y。若然考虑 x 是实数或复数,则 f 的零点集是所有 (x,x) 的集合,是一个代数曲线。事实上所有代数曲线由此而来。
代数基本定理
代数基本定理是指所有一元 n 次(复数)多项式都有 n 个(复数)根。
多项式的几何特性
多项式是简单的连续函数,它是平滑的,它的微分也必定是多项式。
泰勒多项式的精神便在于以多项式逼近一个平滑函数,此外闭区间上的连续函数都可以写成多项式的均匀极限。















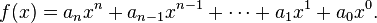



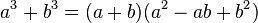
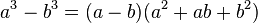



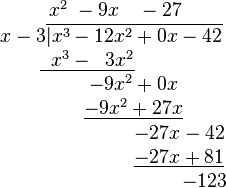

















 826
826

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








