题目:题目链接,给出二叉树的后序、中序,求层序。
首先这里有个知识点,就是二叉树的搜索(遍历)分为几种:
- 前序,pre order
- 中序,in order
- 后序,post order
- 层次遍历,level order
其实前三种都属于二叉树的深搜(DFS),层次遍历就是广搜(BFS)。在这里要注意的是,如果想要唯一确定一棵二叉树,至少要给出“中序”;如果只知道前序、后序,是不能唯一确定一棵树的。
解题思路:根据给出的2个序列,建立起一棵二叉树。然后再对这棵树进行BFS。所以关键是建树的过程。
在这道题中,是根据后序和中序,去确立一颗树。其实算法的过程可以说是在模拟我们在纸上思考的过程。
根据PAT网站给出的测例,说明一下这个过程。
测例:
后序: 2 3 1 5 7 6 4
中序: 1 2 3 4 5 6 7算法过程:
( 从整个序列开始)先看后序,最后一个是4,那么根结点就是4。然后在中序那里找到4,把中序分成3部分:123、4、567,分别对应左子树,根,右子树。然后根据子树的结点数(左子树有3个点,右子树有3个点),后序也相应地分成3部分:231、 576、 4:
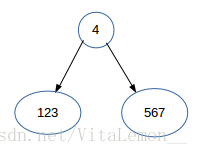
然后对左子树子序列(“123”)和右子树的子序列(“567”)递归地进行上述过程,便构造出一棵树了。
如果看到这里还不是太明白,我们可以把该算法再走一会儿:
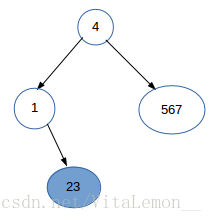
我们先走左子树。中序为:123,后序为:231。同样,在后序中发现“1”是局部根结点,那么只剩下右子树“23”。如图:
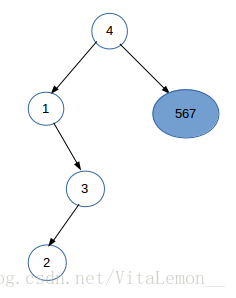
中序的“23”对应后序的“23”,那么“3”就是局部根结点,“2”就是其左结点了:(这里的左子树只剩下一个结点,整棵树的左边的递归终止)
剩下就是整棵树的右边“567”了,相信大家已经会自己演绎了,那剩下的就是代码的事情了。
代码:(代码粗糙,不过我会以注释的形式去说明一些关键的部分):
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
/* 二叉树的结点 */
struct Node {
int element;
Node* left;
Node* right;
Node() {
element = -1;
left = right = NULL;
}
Node(int e, Node* l = NULL, Node* r = NULL) {
this->element = e;
this->left = l;
this->right = r;
}
};
/* 二叉树。在Node层上再抽象出BTree一层是为了方便操作 */
class BTree {
public:
BTree() {
root = NULL;
}
BTree(Node* node) {
root = node;
}
~BTree() {
clear(root);
}
vector<int> bfs() const {
Node* tmp = root;
vector<int> resultList;
queue<Node*> Q;
Q.push(tmp);
while (!Q.empty()) {
Node* curNode = Q.front();
Q.pop();
// current
resultList.push_back(curNode->element);
// next
if (curNode->left != NULL) {
Q.push(curNode->left);
}
if (curNode->right != NULL) {
Q.push(curNode->right);
}
}
return resultList;
}
private:
Node* root; // 存储根结点
/* 注意,释放一棵树的堆内存,需要采取后序的方式 */
void clear(Node* root) {
if (root == NULL) return;
clear(root->left);
clear(root->right);
delete root;
}
};
const int CASE_NUM = 1;
const int MAX_NODE_NUM = 30;
int nodenum;
int postOrder[MAX_NODE_NUM], inOrder[MAX_NODE_NUM];
/* 递归地 建立起一棵二叉树 */
Node* buildTree(int postLeft, int postRight, int inLeft, int inRight) {
if (inRight <= inLeft || postRight <= postLeft) return NULL; // 递归的终止条件
int rootElement = postOrder[postRight - 1]; // 后序子序列中最后一个就是根结点
Node* ret = new Node(rootElement); // 分配内存,建立根结点
int pos;
// 然后在中序子序列中定位根结点的位置
for (int i = inLeft; i < inRight; ++i) {
if (rootElement == inOrder[i]) {
pos = i; // pos就是根结点的位置
break;
}
}
// 因为在中序中,根结点一旦确定,那么它左边的序列就是左子树,右边的序列就是右子树
int leftCount = pos - inLeft; // 左边序列的长度
int rightCount = inRight - pos; // 右边序列的长度
ret->left = buildTree(postLeft, postLeft + leftCount, inLeft, pos); // 递归:对左子树再进行建树的过程
ret->right = buildTree(postLeft + leftCount, postRight - 1, pos + 1, inRight); // 递归:对右子树进行建树
return ret; // 返回当前根结点(局部根结点)
}
int main() {
int casenum = CASE_NUM;
while (casenum--) {
// 处理输入
cin >> nodenum;
for (int i = 0; i < nodenum; ++i) {
cin >> postOrder[i];
}
for (int i = 0; i < nodenum; ++i) {
cin >> inOrder[i];
}
// 建树
Node* root = buildTree(0, nodenum, 0, nodenum);
BTree* bTree = new BTree(root);
// 按照格式输出结果
vector<int> levelOrder = bTree->bfs();
for (int i = 0, len = levelOrder.size(); i < len; ++i) {
cout << levelOrder[i];
if (i == len - 1) {
cout << endl;
} else {
cout << ' ';
}
}
delete bTree; // 记得释放堆内存哦!
}
return 0;
}





















 381
381











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








