排序算法：冒泡排序

冒泡法排序思路：
      先将序列中的第一个记录R1与第二个记录R2比较，若R1>R2,则把R1，R2交换位置，然后处理新的R2，R3，直到Rn-1和Rn也做了上述操作，此时就完成了一趟排序，由上述的操作可知，最大的记录将被交换的第n位上。在执行下一趟排序时，因为前一趟排序已将序列最大值排到最后，所以只需进行n-1次比较，即将第二大的记录交换到第n-1位。依次类推，直到做完n-1趟比较，序列将变为有序序列。
      由于上述的排序过程中，越大的元素会经由交换慢慢“浮”到序列的尾部，因此称其为冒泡法排序。

以长度为6的序列 {6，3，5，4，1，2} 的冒泡排序过程做示范：
第一趟排序：3 5 4 1 2 [6] （6浮到尾部）
第二趟排序：3 4 1 2 [5 6] （5浮到尾部）
第三趟排序：3 1 2 [4 5 6] （4浮到尾部）
第四趟排序：1 2 [3 4 5 6] （3浮到尾部）
第五趟排序：1 [2 3 4 5 6] （没有数字可以交换）

由上述排序过程可以看出一个问题，序列在第四趟排序时已经有序，但仍然需要进行第五趟比较。因此可以加上一个标志位，当某一趟排序完成后没有发生交换，则置该标志位为true，代表序列已经有序，无需继续比较。

本文根据上述的冒泡排序思路以及改良的冒泡排序思路给出C++与Java的代码实现，并且使用Java对两种冒泡算法进行性能比较。

C++代码:

//交换两个整数
void swap(int *a, int *b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}
//基本冒泡法
void bubbleSort(int *arr, int length)
{
    if (arr == NULL || length <= 0)return;
    for (int i = 0; i < length - 1; ++i)
    {
        for (int j = 0; j < length - 1 - i; ++j)
        {

            if (arr[j + 1] < arr[j])
            {
                swap(&arr[j], &arr[j + 1]);
            }
        }
    }
}

//改良的冒泡法
void bubbleSort(int *arr, int length)
{
    if (arr == NULL || length <= 0)return;
    bool noswap;
    for (int i = 0; i < length - 1; ++i)
    {
        noswap = true;
        for (int j = 0; j < length - 1 - i; ++j)
        {

            if (arr[j + 1] < arr[j])
            {
                ++::count;
                swap(&arr[j], &arr[j + 1]);
                noswap = false;
            }
        }
        if (noswap)break;
    }
}

Java代码：

private void bubbleSort(List<Integer> list) {
    int length = list.size();
    for (int i = 0; i < length - 1; ++i) {
        for (int j = 1; j <= length - 1 - i; ++j) {
            if (list.get(j - 1) > list.get(j)) {
                swap(list, j, j - 1);
            }
        }

    }

改进后的冒泡排序：

private void improvedBubbleSort(List<Integer> list) {
    int length = list.size();
    boolean noswap = false;
    for (int i = 0; !noswap && i < length - 1; ++i) {
        noswap = true;
        for (int j = 1; j <= length - 1 - i; ++j) {
            if (list.get(j - 1) > list.get(j)) {
                swap(list, j, j - 1);
                noswap = false;
            }
        }

    }
}

使用完全相同的元素为整数的List对两种冒泡排序算法进行性能测试结果如下：

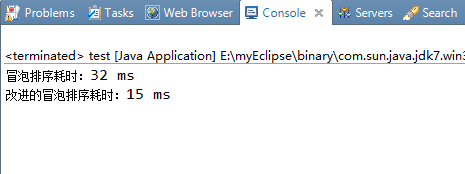
序列元素个数为1000时：

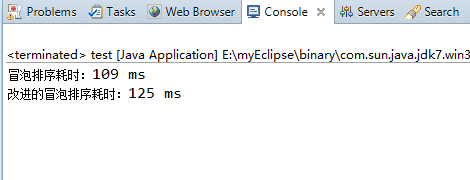
序列元素个数为5000时：

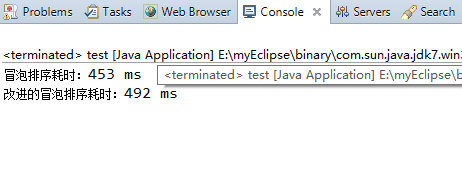
序列元素个数为10000时：

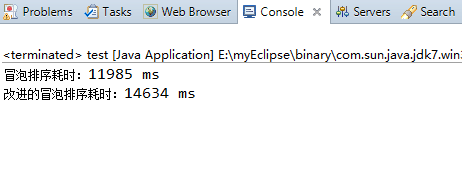
序列元素个数为50000时：

可以发现其实改进的冒泡排序算法在实际中的效率反而不如原来的冒泡法，这其实是因为改进的冒泡排序算法在每一步排序过程中都增加了对布尔变量noswap的开销，包括赋值操作、比较操作，由于冒泡排序算法的时间复杂度是O(n^2)级别的，再细微的开销也会随着n值的递增而逐渐放大。（就像人生一样啊“千里之堤毁于蚁穴”，细节是魔鬼！）

ps：其实这里的性能比较是非常粗糙的，因为程序在实际运行过程中，还要考虑CPU中进程的运行状态，因此本文的测试方法记录的时间仅仅能作为一个参考。如果要更加细致的测试，可以自己写一些更精密的测试方法，例如可以让两种算法使用相同的测试数据，各执行100次，取其平均效率作为评价其排序表现的依据，或者在测试过程中，保证CPU分配的公平性，不要运行其他可能会抢占系统资源的程序等等。

冒泡法暂时就讲到这里了，其实还有很多关于冒泡法的变形，这里就不再一一叙述了。