最长公共子序列(LCS)问题分析

最长公共子序列(LCS)网上的资料很多，而且也可以算是动态规划里面的一个基本问题，它体现了许多动态规划的特性，算法导论这本书也给出了很详细的说明。

要写好动态规划其实还是有些难度，网上也很多相关的资料，这里我也就只是想写一篇自己个人的笔记，整理下自己学的一些东西。

问题描述

输入：对于一个字符串(序列)，将其中若干个字符(元素)去除后剩余的字符串(序列)，我们称之为子序列(注意：子序列与子串是两个不同的概念，子串是原有序列中某个长度的连续元素)，现在给定两个字符串，公共子序列则是指两个字符串的相同的子序列

输出：最长的子序列

问题分析

分解问题

如果要直接开始求解，其实还是有些复杂的，即使我们知道使用动态规划可以解决这个问题，后面的分析我们可以发现，要得到这个答案，我们需要做的事情很多。所以我们将这个过程一步步分解。

我们先试着去求解两个最长子序列的长度，后面再考虑如何去构造这个子序列，这样难度可以得到减少。

当然，为什么我们会先考虑求解两个子序列的长度，这就需要自己想了(其实我自己也想不明白)。

定义状态与解的描述

动态规划，说白了也是一类搜索问题。

使用动态规划技术去分析问题，需要特定的步骤，特定的分析手段，这个在《算法导论》书上有比较详细的分析。

首先，我们需要描述这个问题的最优子结构，也就是常说的状态。

我们使用三元组{a(m), b(n), l(m,n)}来描述，a(m)和b(m)为长度分别为m和n的子序列a、b，l(m,n)表示两者的最长公共子序列的长度。

然后，我们就可以知道，如果我们已经知道a(m)和b(n)的最长公共子序列长度为l(m,n)，a(m+1)和b(n)的最长公共子序列长度为l(m+1,n)，以及a(m)和b(n+1)的最长公共子序列长度为l(m,n+1)。

那对于a(m+1)和b(n+1)的最长公共子序列长度为l(m+1,n+1)的最长公共子序列则有三种情况：

当a[m+1]==b[n+1]时，l(m+1,n+1) = l(m,n)+1 

当a[m+1]!=b[n+1]时，l(m+1,n+1) = max{l(m+1,n), l(m,n+1)}

最后得到的状态转移方程(看成一个递归方程也行)就如下图所示(注：该图取自网络，所使用的字符和下标和上文不同，但是思路相同)

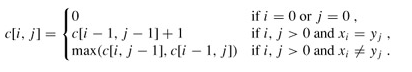
这样我们可以获得一个如下的状态图。

这个状态图有一些很特殊的点，这也是动态规划的一些特点：

(1) 问题的解其实在树的根部

(2) 根部的解需要由其子节点的解进行合并而成

(3) 叶子节点是一个最小子问题，可以理解成我们可以使用肉眼观测出结果的一个问题规模，这很重要，如果使用递归实现，我们很容易发现这就是递归的终止条件。

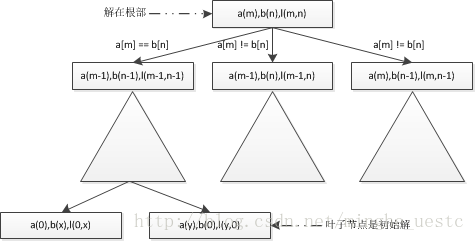
求解过程

通过上述的过程，我们找到了一种描述解的一种方法，那剩下的问题就是，如何去获得这个解。我们知道一个特性，就是解在于整棵树的根部，叶子节点则是我们的初始解。

剩下的问题就是我们的搜索策略问题，对于动态规划，一般存在两种策略——递归、递推。

能够使用递推进行实现的原因在于解在于这个树的根部，而我们却很容易知道叶子节点的解是多少，这样，我们使用“自底向上”的策略，我们就可以一层层的去靠近最终解。如果最终解在叶子节点上，递推这种方法就没办法了。

幸运的是，因为动态规划技术的特性，所有动态规划问题(最少是我遇到的所有动态规划问题)，都符合上述的所说的特点，所以我们都可以使用递推的方式进行实现。

所以我们求解动态规划，一般会选择递推进行实现。

接下来，我们先讨论递归实现时候的分析过程。

递归实现下的剪枝(1)

一种暴力的做法就是，我们将整棵树遍历一遍就可以得到答案，但是这种明显不现实。认真观察上图，我们发现，