对多元函数在某点的各个自变量分别求偏导数,并将各偏导h数作为向量的分量,此向量即为函数在此点的梯度,表示函数因变量(方向导数)变化最快的方向。当梯度前的符号为“+”时,函数值向最大值方向移动,符号为“-”时,函数值向最小值方向移动。
在求解线性回归模型及逻辑回归模型的代价函数最值时,梯度下降法具有广泛的应用性,对θ参数矩阵进行迭代,直至得到关于θ的函数(代价函数)局部最优解,即最值。举个栗子,假如你想下山(其实是进山谷啦),站在高处,你要思考该走哪一个方向,使得你下山的路程最短,每走一步,你便需要思考一次,这样当你到达山谷底部时,所走的路径便是速度最快的路线。
梯度下降的一般公式为:
α为学习率,表示每次迭代的幅度,函数J(θ)为模型的代价函数,减号右边的除去学习率的项为梯度,即代价函数对各个θ的偏导数。当减号右边的项小于预设的δ时,迭代结束。
上述公式的矩阵表示式为:
对于参数矩阵的迭代,可用所有的实例进行,称为批量梯度下降(BGD),但当数据量过大时显然影响速度,或是每次仅对1个实例进行迭代,称为随机梯度下降(SGD),迭代速度快,但准确性堪忧,可能不会很快地得到局部最优解。折中的办法是小批量梯度下降(WBGD),对于所有实例中的一部分进行迭代。
在求解代价函数的过程中,一般会使用最小二乘法或梯度下降法。前者是计算解析解,后者是迭代求解,所以在实例、特征较少,关于实例的逆矩阵存在时,前者速度快、具有较大优势;而在不满足上述条件(大多情况下都不满足)的情况下,梯度下降法就应该是要选择的方法了。PS:牛顿法、拟牛顿法也是迭代求解,并且比梯度下降法收敛到局部最优值要快,但每次迭代的时间较长。







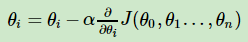














 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








