【经典算法】详解 KMP 算法

KMP算法是通过分析模式字符串，预先计算每个位置发生不匹配的时候，所需GOTO的下一个比较位置，整理出来一个next数组，然后在上面的算法中使用。

简单的说来，原始的字符串匹配算法是将子串中的字符一个一个的同母串进行比较，如果相同则向前推移比较下一位，如果遇到不相同的，则将字串的第一个字符同上次字串与母串比较位置的下一个位置字符进行比较。时间复杂度为O(nm)。

/*
假定字符串在数组中：char S[n]，
模式串在另一数组中：char T[m]
*/
for (int i = 0; S[i] != '\0'; ++i)
{
	for (int j = 0; S[i + j] != '\0' && T[j] != '\0' && S[i + j] == T[j]; ++j);
	if ('\0' == T[j])
		//found a match
}

即失配时，子串要回溯要起点，母串也要回溯与子串相等的长度，然后对下一个位置开始进行匹配。下面这样一种情况
                                    

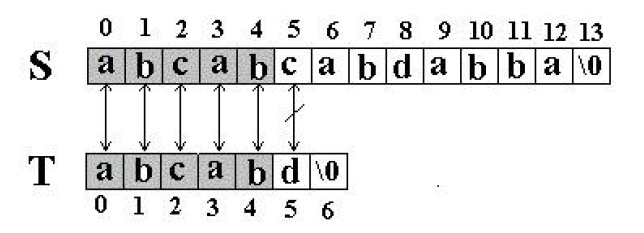
S[5] 与 T[5] 失配，然后下一轮匹配就从 T[0] 与 S[1] 开始。也就是说当这样一个失配发生时，T 下标必须回溯到开始，S 下标回溯的长度与 T 回溯的长度相同，然后 S 下标增 1，然后再次比较。直到最后匹配完毕，或匹配成功。

事实上上面这种情况，对于字串 T，由于 T[5] 的前面两个字符与 T 的开始两个字符相同，并且 T[5] 的字符与开始的两个字符后面的那个字符（开始的第三个字符）不同（后面解释），如下图

                                                       

结合上面，这样下一轮匹配完全可以从，S[5] 和 T[2] 开始匹配。因为 S[5] 前面的几个（视与T匹配的程度）字符都是与 T 匹配过的，也就是 T 失配位置的前面几个（视程度）和 S 失配位置前同样个数的字符相同的，如果 T 开始位置恰巧和 T 失配位置前几个字符相同，就可以跳过这几个字符的匹配。回到前面，为什么必须T[5] 的字符与开始的两个字符后面的那个字符（开始的第三个字符）不同呢？很简单，T[5] 恰好是失配字符，如果与开始的第三个字符相同，那也必然是失配的情况。

上面已经出现了KMP算法的影子了，KMP 算法的核心思想是利用已经得到的部分匹配信息来进行后面的匹配过程。

在本文前面列举的那个原始匹配算法，通过算法里面的内循环我们可以获知许多关于字符串的信息，凡是匹配，就说明母串中的该字符或该段字符与子串相同，这样我们可以转到子串去分析，构造一个 next 数组：next [i] = j；表示字符模式子串 T[0 ~ i-1] 中前缀和后缀字符相同的长度为 j（最大长度），即 T[0 ~ j-1] == T[i-j ~ i-1]。当模式中，子串第 k 个字符与主串中相应字符失配时，在模式中子串需要重新和主串中该字符进行比较的字符的位置为 next[k]。

尤其需要注意的是：上面说的 T[0 ~ i-1] 中前缀和后缀字符相同，指的是以子串 T 的每个子部分为目标的前缀和后缀字符相同，然后慢慢向后移，扩大子部分。就是T[0~1]，T[0~2]，T[0~3]，……T[0~i-1] 的前缀和后缀字符相同的个数记录在next 数组中。

就是说，当子串与母串发生失配时，母串并不需要回溯，依旧将失配位置字符与字串的某个位置的字符进行匹配，至于是与字串的哪个位置的字串进行匹配，就是后面讨论的重点了。从前面的分析可以看出一些端倪，当发生失配时，子串重新匹配的字符位置取决于子串失配位置（假定失配字符为T[i]）前部分 T[0~i-1] 中的前缀与后缀的相等部分的最大长度。因为既然匹配到了 T[i]，表明 T[0 ~ i-1] 与母串是匹配的，如果 T[0 ~ j-1] == T[i-j ~ i-1]，那么完全可以从 T[j] 开始与母串失配位置开始匹配，前面部分肯定是匹配的。

通过上面分析，关键点就落在了求 next 数组上。next 数组记录每次失配时，子串需要重新和主串中该失配字符进行比较的字符的位置。

 这里参照 Knuth-Morris-Pratt 于1996 年发表在ICS上的论文，next 数组的起始位置定为-1，结合上面的分析，我们先来看一个子串模式，这里再次说明是失配字符位置的前面部分字符为目标。得出 next 数组，实质就是得出当 T[i] （第 i 个字符）失配时（i = 1,2,……），下一次将匹配的位置为 next[i]。

示例一：

char *T = "abcabdabcaaacccc";   

next[0] = -1; i = 0，第 1 个字符前面没有字符，所以为-1； 

next[1] = 0; i = 1，第 2 个字符前只有 a，肯定为0；

next[2] = 0; i = 2，第 3 个字符前有 ab，前缀为a，后缀为b，不相等，也为0；

……

next[4] = 1; i = 4，第 5 个字符前面有 abca，前缀与后缀相等的最大长度为1

next[5] = 2; i = 5，第 6 个字符前面有 abcab，前缀与后缀相等的最大长度为 2（ab，abc != cab）

next[6] = 0; i = 6，第 7 个字符前面有 abcabd，虽然有ab == ab，但是 abc != abd，即必须保证第 i-1 个字符是匹配（模式子串本身前后缀匹配）的，否则，呵呵，前面再怎么匹配也白费，照旧为 0。

…… 以此类推，最后得出 next[] = {-1,0,0,0,1,2,0,1,2,3,4,1,1,0,0,0}

去掉 next[0] = -1，后面共有15个元素，恰好是模式子串长度 i 减1。失配字符前面的前后缀最大相等长度。

示例二：

示例一没有给出失配情况下，next 数组的求值，这里为方便演示，修改一下模式子串

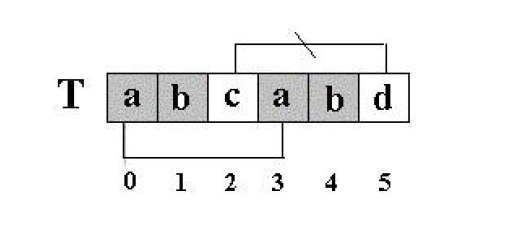
char *T = "abcabac";

next[0 ~ 5] = {-1, 0, 0, 0, 1, 2}; //next[i] = j 表示子串前面 i 个字符构成的字符串前后缀相等的最大长度为 j。abcab最大相等为 2

到了第6个字符就出现失配了，abcaba 中 abc != aba，那么 next[6] 该为多少呢？

根据前面匹配信息来，next[5] = 2，表示前面5个字符前后缀有两个字符相等，即前面5个字符构成的字符串首两个字符与第6个字符的前两个字符是匹配的，那么我们就跳转到首两个字符，去获取首两个字符单独的匹配情况。如果首两个字符匹配（相同字符，next[2] = 1），那么就只需拿第 2 个（T[1]）字符与第 6 个字符匹配，如果不匹配（next[2] = 0），那么第 6 个字符就只能同第 1（T[0]） 个字符比较匹配了。总的说来就是T[6] 与T[next[next[5]]] 去比较匹配。

对于模式子串（求next数组该子串既是母串又是子串），即使起始字符与最后字符不相等，其最大长度也不一定为0，如next[5]，所以求解next数组不能简单的由后往前推求最大相等长度，而需要借助之前结果的递推求解。比如 next[4] = 1，我们就知道前面四个字符最大前后缀相等长度为1，或者 next[i] > 0，我们就知道前面 i 个字符存在前后缀相等（长度为 next[i]）的字符，我们就可以直接去匹配第 i+1 个字符与第 next[i]+1 个字符。比如上面 next[4] = 1，那么下一步就是那第5个字符去匹配第2个字符。这个字符串同数组一样是从0位置开始的。

上面是求 next 数组的大致思路，得到 next 数组只是 KMP 中的一部分，但是是最关键的一部分。下面根据上面分析给出程序实现：

	int index = 0;
	next[0] = -1;
	for (int i = 0; pattern[i] != '\0'; ++i)
	{
		index = next[i] + 1;
		next[i + 1] = index;   //匹配时，next[i+1]递增

		/*在前面存在匹配，但后面出现失配时*/
		while (index > 0 && pattern[i] != pattern[index - 1]) //index-1 == next[i]
		{
			index = next[index - 1] + 1;      //index = next[next[i]] + 1，加1是为了符合循环
			next[i + 1] = index;              //失配时更新next[i+1]
		}
	}

可针对上面进行优化（KMP论文）

	next[0] = -1;
	for (int i = 0; pattern[i] != '\0'; ++i)
	{
		next[i + 1] = next[i] + 1;

		while (next[i + 1] > 0 && pattern[i] != pattern[next[i + 1] - 1] /*patter[next[i]]*/)
			next[i + 1] = next[next[i + 1] - 1]/*next[next[i]]*/ + 1;	
	}

得到 next 数组，子串与母串匹配时，next 数组中的数值意义表示：

• next[i] = -1，表示母串 S[m] 已经和 T[0] 比较过了且不相等，下一轮比较 S[m+1] 和 T[0]
• next[i] = 0，表示比较过程中产生了不相等，下一轮比较 S[m+1] 和 T[0]
• next[i] = j > 0，表示 S[m] 的前 j 个字符与 T 中的开始 j 个字符相等，下一轮比较 S[m] 和 T[j]

下面根据上面分析，给出 KMP 算法完整程序：

int kmp_search(const char *target, const char *pattern)
{
	const int target_len = strlen(target);
	const int pattern_len = strlen(pattern);
	int *next = new int[pattern_len];

	/*Get next array*/
	next[0] = -1;
	for (int i = 0; pattern[i] != '\0'; ++i)
	{
		next[i + 1] = next[i] + 1;

		while (next[i + 1] > 0 && pattern[i] != pattern[next[i + 1] - 1])
			next[i + 1] = next[next[i + 1] - 1] + 1;
	}

	/*search*/
	int target_index = 0;
	int pattern_index = 0;

	while (target_index < target_len && pattern_index < pattern_len)
	{
		if (pattern[pattern_index] == target[target_index])  //匹配
		{
			++pattern_index;
			++target_index;
		}
		else  /*失配时*/
		{
			pattern_index = next[pattern_index];   //更新模式子串待匹配位置
			if (-1 == pattern_index)  //-1表示target[target_index]和pattern[0]已经比较过了
			{                         //只有next[0] == -1
				pattern_index = 0;    //下一轮直接比较pattern[0]和target[target+1]
				++target_index;       
			}
		}
	}

	/*return position*/
	if (pattern_index == pattern_len)
		return target_index - pattern_index;
	else
		return -1;
}

时间复杂度分析：

从上面程序可以看出，KMP 的时间复杂度主要由两部分组成，一个是 next 数组的计算，一个是子串与母串的比较。前一个的时间复杂度为O(m)，后一个的时间复杂度为O(n)，所以KMP 算法总的时间复杂度为O(n+m)。

参考资料：

        Knuth-Morris-Pratt string matching