图及其操作（C语言版）

图及其操作（C语言版）

标签（空格分隔）： 未分类

---

图的定义和性质：

1. 定义: 图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,R)，其中，G表示一个图，V是图G中顶点的集合，R是图G中边的集合。

2. 顶点：在图中的数据元素通常叫做顶点。

3. 弧头/弧尾：若 <v,w>∈VR <script type="math/tex" id="MathJax-Element-1"> \in VR</script>则 <v,w> <script type="math/tex" id="MathJax-Element-2"> </script>表示从 $v$到 $w$的一条弧，且称 $v$为弧尾或初始点，称$w$为弧头或终端点。

4. 有向图：若图中的边是有向的，即 <v,w>∈VR≠<w,v>∈VR <script type="math/tex" id="MathJax-Element-7"> \in VR \neq \in VR</script>此时的图称为有向图。

5. 无向图：若 <v,w>∈VR <script type="math/tex" id="MathJax-Element-8"> \in VR</script> 必有 <w,v>∈VR <script type="math/tex" id="MathJax-Element-9"> \in VR</script>,即 $VR$是对称的，则以无序对 $(v,w)$代替两个有序对，表示v,w之间的一条边，此时的图称为无向图。

6. 完全图：若用n表示图中的顶点数，用e表示图中弧或者边的数目，在下边的讨论中，我们不考虑顶点到其自身的边或者弧。

   • 对于无向图来说：$0\le e \le \frac{1}{2}n(n-1)$,有$\frac{1}{2}n(n-1)$条边的无向图称为完全图
   • 对于有向图来说：$0\le e \le n(n-1)$,有$n(n-1)$条弧的有向图称为有向安完全图。

7. 稀疏图/稠密图：有很多条边或者弧的图称为稠密图，反之称为稀疏图$例如：(e\lt n\log{n})$

8. 权：有时边或者弧有和他相关的数，这种与图的边或者弧相关的数叫做权。这些权可以表示一个顶点到另一个顶点的距离或者消耗。

9. 网：带权的图称为网。

10. 子图：假设有两个图$G=\{V,\{R\} \}$和$G^`=\{ V^`,\{R^`\}\}$，如果$V^` \subseteq V$且$R^` \subseteq R$,则称$G^`$为$G$的子图

11. 邻接点：

    • 对于无向图：$G=\{V,\{R\} \}$,如果边$(v,v^`) \in R$,则称顶点$v$ 和互为邻接点$v^`$，边$(v,v^`)$依附于顶点$v$和$v^`$。或者说边$(v,v^`)$和顶点$v$和$v^`$相关联。

    • 对于有向图：$G=\{V,\{A\} \}$,如果弧 <v,v1>∈A <script type="math/tex" id="MathJax-Element-34"> \in A</script>,则称顶点 $v$邻接到顶点$v^`$，顶点 $v^`$邻接到顶点 $v$,弧$<v,v^`>$和顶点 $v$，$v^`$相关联。

    • 无向图顶点的度：在无向图中，顶点v的度是和顶点v相关联的边的数目，记做$TD(v)$

    • 有向图顶点的度：

      • 入度：在有向图中，顶点v的入度是指以顶点v为头的弧的数目
      • 出度：在有向图中，顶点v的出度是指以顶点v为尾的弧的数目

    • 顶点，边(弧)，度之间的关系：一般的，如果顶点$v_i$的度记为$TD(v_i)$，那么一个有$n$个顶点，$e$条边或者弧的图，满足如下关系：

      $$e=\frac{1}{2} \sum_{i=1}^nTD(v_i)$$

    • 图的路径：无向图$G=\{V,\{E \} \}$中从顶点$V$到顶点$V^`$的路径是一个顶点序列$(v=v_{i,0},v_{i,1},...,v_{i,m}=v^`)$其中$(v_{i,j-1},v_{i,j}) \in E,1 \le j \le m$。如果G是有向图，则路径也是有向的。

    • 路径的长度：路径上边或者弧的数目

    • 回路/环第一个顶点和最后一个顶点相同的路径称为回路或者环。除了第一个和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或者简单环。

    • 连通图：在无向图G中，如果从顶点$v$到顶点$v^`$有路径，则称$v$和$v^`$是连通的。若对于图中任意两个顶点$v_i$、$v_j\in V$，$v_i$和$v_j$都连通，则称G是连通图。

    • 连通分量：无向图中的极大连通子图称为是该图的连通分量。

    • 强连通图：在有向图G中，如果对于每一对$v_i,v_j \in V ,v_i \neq v_j$ ,从对$v_i到v_j$和从$v_j到v_i$都存在路径，则称G是强连通图。

    • 强连通分量：有向图中的极大连通子图称作有向图的强连通分量。

    • 连通图的生成树：一个连通图的生成树是一个极小连通子图，他含有图中的全部顶点，但是只含有构成一颗树的$n-1$条边。

    • 性质：

      • 一颗有n个顶点的生成树有且只有n-1条边
      • 如果一个图有n个顶点和小于n-1条边，则是非连通图。若多于n-1条边，则一定有环。
      • 如果一个有向图恰有一个顶点的入度为0，其余顶点的入度均为1，则是一颗有向树。

图的存储结构：

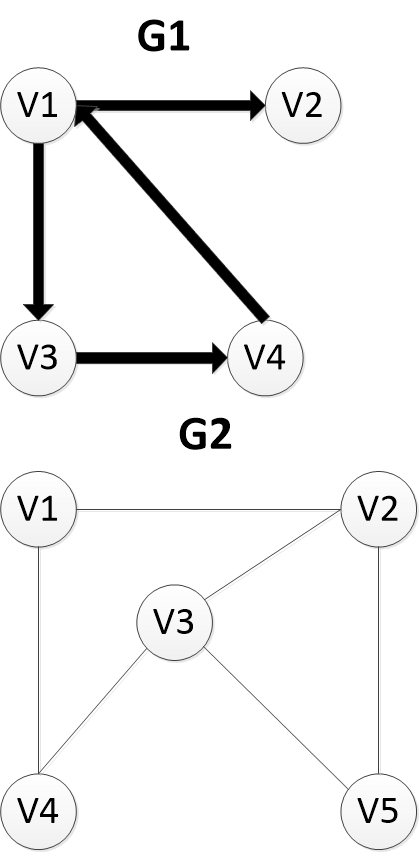
以这两个图为例：

1.数组表示法：

用两个数组分别存储数据元素(顶点)的信息和数据之间的关系(边或弧)的信息。

/**数组表示法（邻接矩阵）**/

#define INFINITY INT_MAX//整数类型最大值
#define MAX_VERTEX_NUM 20//最大顶点个数
typedef enum{ DG,DN,uDG,UDN} GraphKind;//{有向图，有向网，无向图，无向网}

typedef struct ArcCell{
    VRType adj;//弧或者边的类型：对于无权图，用0或者1表示是否相邻
               //对带权图，则为权值类型
    InfoType *inform;//改弧相关的信息指针
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];

typedef struct {
    VertexType vexs[MAX_VERTEX_NUM];//顶点向量
    AdjMatrix arcs;//邻接矩阵
    int vexNum,arcNum;//图的当前顶点数量，边或者弧数量
    GraphKind kind;//图类型
}MGraph;

上边两种图的邻接矩阵表示法的示例：

$$G1.arcs=\begin{bmatrix} 0& 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 &0 & 0 \end{bmatrix}$$

$$G2.arcs=\begin{bmatrix} 0& 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 &1\\ 0 & 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 \end{bmatrix}$$

2.邻接表：

邻接表是图的一种链式存储结构。在邻接表中，对图中的每个顶点建立一个单链表，第$i$个单链表中的结点表示依附于顶点$v_i$的边（对有向图是以顶点$v_i$为尾的弧）。每个结点由3个域组成，其中邻接点域（adjvex）指示指示与顶点$v_i$邻接的点在图中的位置，链域（nextarc）指示下一条边或者弧的结点，数据域（info）存储和边或者弧相关的信息(如权值等)。在表头结点中除了设有链域（firstarc），指向链表中的第一个结点外，还设有存储顶点$v_i$的名或者其他有关信息的数据域（data）。

/**邻接表表示法**/
#define INFINITY INT_MAX//整数类型最大值
typedef struct ArcNode{//弧结点
    int adjvex;//改弧所指向的位置
    struct ArcNode *nextArc;//下一条弧指针
    InfoType *info;//该弧相关信息的指针
}

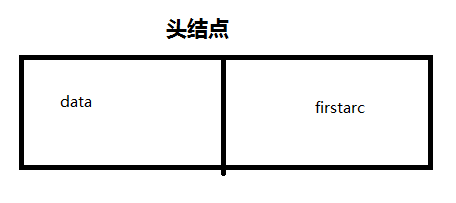
typedef struct VNode{//表头结点
    VertexType data;//顶点信息
    ArcNode *firstArc;//依附该节点的第一条弧结点
}VNode,AdjList[MAX_VERTEX_NUM];

typedef struct {//邻接表
    AdjList vertices;//图的顶点数组
    int verNum,arcNum;//弧的当前顶点数和弧数
    int kind;//图类型
}ALGraph;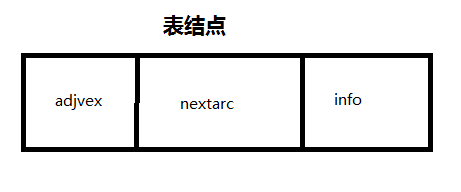

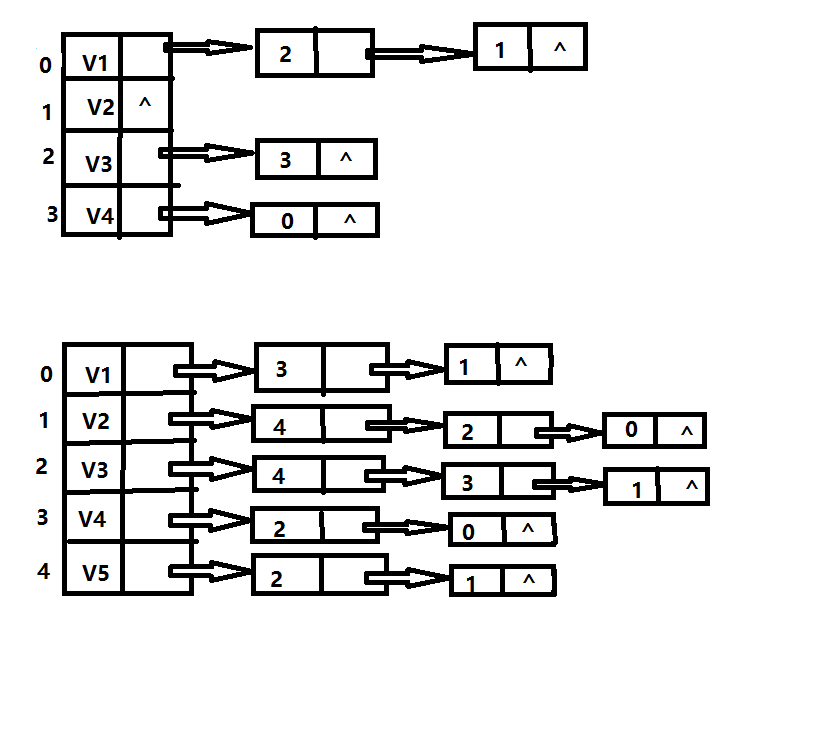
上边两种图的邻接表表示法的示例：

上边的两种存储结构对于无向图和有向图均可适用，而另外的两种存储结构则有所偏向。

3.邻接多重表（无向图）：

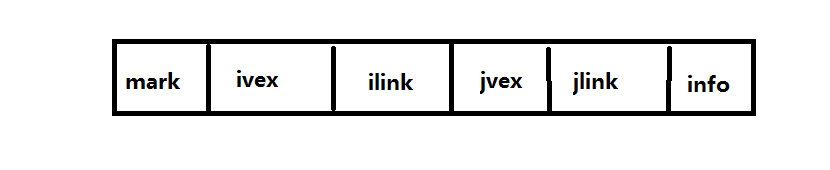
在邻接多重表中，每一条边用一个结点表示，而一个节点由如下所示的六个与组成：

其中mark域为标志域用于标记该边是否被搜索过；ivex和jvex为依附于该边的两个节点在图中的位置；ilink指向于下一条依附于结点ivex的边；jlink指向于下一条依附于结点jvex的边；info为指向该边的信息的指针域。

4.十字链表（有向图）：

在十字链表中，对应于有向图的每一条弧有一个结点，对应每一个顶点也有一个结点。

弧结点：

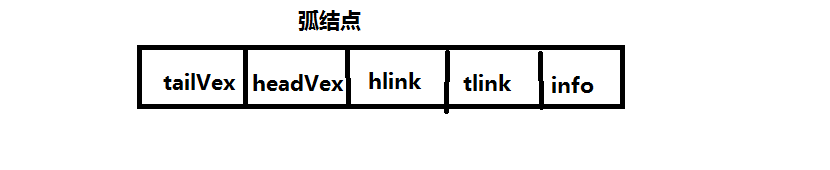
其中tailVex和headVex分别指向弧头和弧尾这两个结点在图中的位置；链域hlink指向弧头相同的下一条弧；tlink指向弧尾相同的下一条弧；info指向该弧的相关信息

顶点结点：

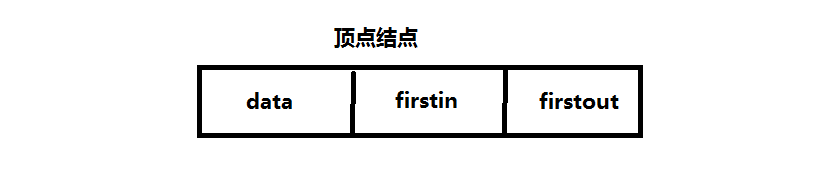
其中data域存储和顶点相关的信息；firstin指向第一个以该顶点为弧头的弧结点；firstout指向第一个以该结点为弧尾的弧结点。

图的遍历：

图的遍历分为两种：深度优先（DFS）和广度优先（BFS）

• 深度优先遍历：

  1. 初始状态是图中的所有顶点都未被访问，则随机选取图中的某一顶点$v$出发，访问该结点；
  2. 然后依次从$v$未被访问的邻接点出发深度优先遍历图（递归），直至图中所有和$v$有路径相通的顶点都被访问到；
  3. 若此时图中仍有未被访问到的结点，则另选一个未被访问到的结点做起点，重复上述步骤，直到图中所有结点都被访问到。

• 广度优先遍历 ：

  1. 初始状态是图中的所有顶点都未被访问，则随机选取图中的某一顶点$v$出发，访问该结点；
  2. 在访问过$v$之后一次访问$v$的各个未被访问的过的邻接点；
  3. 然后从这些邻接点出发依次访问他们的邻接点，并且保证”先被访问的顶点的邻接点先于”后被访问的顶点的邻接点”被访问，直至所有已被访问的顶点的邻接点都被访问。
  4. 若此时图中国仍有顶点未被访问到，则随机选取未被访问的顶点作为起始点，重复上述步骤，直到图中所有的结点都被访问到。

例如：
对于图G（无向图）来说：

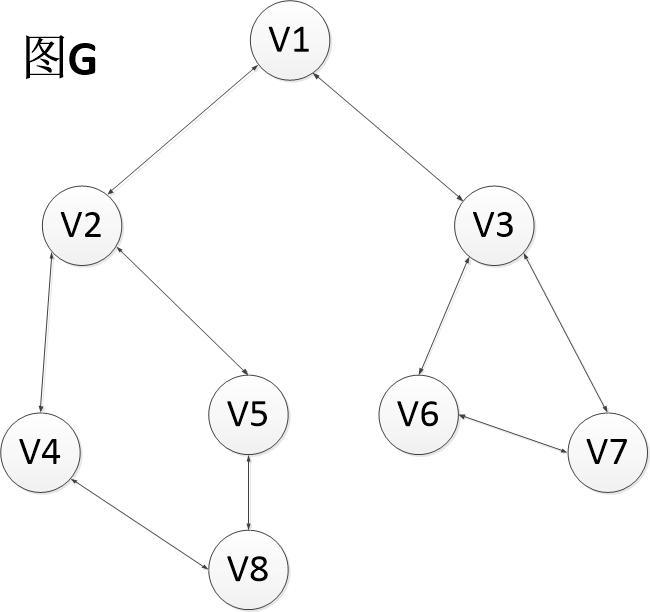
其中一种深度优先遍历序列是：$V_1,V_2,V_4,V_8,V_5,V_3,V_6,V_7$
其中一种广度优先遍历序列是：$V_1,V_2,V_3,V_4,V_5,V_6,V_7,V_8$

注意：因为起始点的不同，所以一个图可能有多种的深度优先和广度优先的遍历序列

图的连通性：

无向图的连通分量和生成树：

• 对于连通图：他的生成树即是他的极小连通子图，只要按照深度优先或者是广度优先的策略进行遍历，即可得到连通图的广度优先生成树或者是深度哟徐爱你生成树。
• 对于非连通图：他的每个连通分量中的顶点集，和深度优先遍历（或者是广度优先）时走过的边一起构成若干颗生成树，这些连通分量的生成树组成非连通图的生成森林。

有向图的强连通分量：

1. 在有向图G上，从某个顶点出发沿以该顶点为尾的弧进行深度优先遍历，并按照其所有邻接点的搜索都完成（即退出DFS函数）的顺序将顶点排列起来。
2. 在有向图G上，从最后完成搜索的顶点出发，沿着以该顶点为头的弧作逆向的深度优先遍历，若此次遍历不能访问到有向图中的所有顶点，则从余下的顶点中最后完成搜索的那个顶点出发，继续做逆向的深度优先遍历，以此类推，直到有向图中所有的顶点都被访问到为止。
3. 此时得到的多个顶点集就是该有向图的多个强连通分量的顶点集。

最小生成树：

构造连通网的最小代价生成树的问题就是图的最小生成树问题。一颗生成树的代价就是树上各边的代价之和。

原理：
构造最小生成树大多都是用了最小生成树的如下性质（MTS）：

假设$N=(V,\{E\})$是一个连通网，$U$是一个顶点集$V$的一个非空子集。若$(u,v)$是一条具有最小权值的边，其中$u \in U,v \in{V-U}$，则必存在一颗包含边$(u,v)$的最小生成树。

常见算法：

• Prim（普里姆）算法：
  假设$N=(V,\{E\})$是连通网，$TE$是$N$上的最小生成树中边的集合。算法从$U=\{u_0\}(u_0 \in V),TE=\{\}$重复执行以下操作：在所有$u \in U,v \in {V-U}$的边$(u,v) \in E$中找出代价最小的一条边$(u_0,v_0)$并入集合$TE$，同时将$v_0$并入$U$,直至$U=V$为止。此时$TE$中必有$n-1$条边，则$T=(V,\{TE\})为N$的最小生成树。

• Kruskal（克鲁斯卡尔）算法：假设$N=(V,\{E\})$是连通网，则令最小生成树的初始状态为只有$n$个顶点而无边的非连通图$T=(V,\{\})$，图中每个顶点自成一个连通分量。在$E$中选择代价最小的边，若该边依附的顶点落在$T$中不同的连通分量上，则将此边加入到$T$中去，否则舍弃此边而寻找下一条代价最小的边。依次类推，直到$T$中所有顶点都在同一个连通分量上为止。

有向无环图的应用：

有向无环图： 一个无环的有向图称为有向无环图（directed acycline graph），简称DAG图。

偏序关系：若集合$X$上的关系$R$是自反的，对称的，传递的，则称$R$是集合$X$上的偏序关系。

全序关系：若$R$是集合$X$上的偏序，如果对于每一个$x,y \in X 必有xRy或yRx$，则称$R$是集合$X$上的全序关系。

拓扑排序：由某个集合上的一个偏序得到该集合上的一个铨叙，这个操作叫做拓扑排序。

AOV-网：用顶点表示事件，用弧表示活动间的优先关系的有向图简称为顶点表示活动的网（Activity On Vertex Network）。

前驱/后继/直接前驱/直接后继在AOV-网中，若从顶点$i$到顶点$j$有一条有向路径，则$i$是$j$的前驱，$j$是$i$的后继。若 <i,j> <script type="math/tex" id="MathJax-Element-122"> </script>是网中的一条弧，则 $i$是$j$的直接前驱， $j$是$i$的直接后继。

AOE-网：与AOV-网相对应的是AOE-网，其中顶点表示事件，弧表示活动，权表示完成活动所需要时间。

拓扑排序算法：

• 在有向图中选择一个没有前驱的顶点直接输出
• 从图中删除该节点和所有以他为尾的弧
• 重复上述两个步骤，直到全部顶点已输出，或者当前图中不存在无前驱的结点为止。
  
  • 若是全部顶点已输出，则完成拓扑排序
  • 若是当前图中不存在无前驱的顶点，则说明有向图中存在环。

最短路径：

从某个顶点到其余各顶点的最短路径：

给定有向带权图G和原点$v$，求从原点$v$到其余各顶点的最短路径。

Dijkstra（迪杰斯特拉）算法（时间复杂度$n^2$）：

• 首先引进一个辅助向量$D$，他的每个分量$D[i]$表示当前所找到的从始点$v$到每个终点$v_i$的最短路径的长度。他的初态为：若从$v到v_i$有弧，则$D[i]$为弧上的权值，否则置$D[i]为\infty$。
  S表示已找到从$v$出发的最短路径的终点的集合，初始状态为空集。
  $arc[i][j]$表示顶点$v_i$到顶点$v_j$的弧的权值。

• 选择$v_j$，使得$D[j] = Min\{ D[i] | v_i \in V-S\}$的路径就是从$v$出发的最短的一条路径，记为$(v,v_j)$

• 若$D[j]+arc[i][j]<D[i]$，则修改$D[i] = D[j]+arc[i][j]$

• 重复操作上述两步$n-1$次，即可得到从顶点$v$到其余各顶点的最短路径。

从某个顶点到其余各顶点的最短路径：

给定有向带权图G，求出每一对顶点之间的最短路径

Dijkstra（迪杰斯特拉）算法（时间复杂度$n^3$）：

每次以一个顶点为原点，重复循环n次Dijkstra算法即可求出每对顶点间的最短路径。

Floyd（弗洛伊德）算法（时间复杂度$n^3$）：

假设求从顶点$v_i$到顶点$v_j$的最短路径。

• 如果从顶点$v_i$到顶点$v_j$存在一条长度为$arc[i][j]$的路径，该路径不一定为最短路径。

• 首先考虑路径$(v_i,v_0,v_j)$是否存在（即判别弧$(v_i,v_0)和(v_0,v_j)$是否存在）。若存在，则比较$(v_i,v_j)和(v_i,v_0,v_j)$的路径长度，选取路径长度小的的路径，作为从$v_i$到$v_j$中间顶点下标序号不大于0的最短路径。

• 如果在路径上再增加一个点$v_1$，也就是说，如果$(v_i,...v_1)和(v_1,...v_j)$分别是当前找到的中间顶点下标序号不大于0的最短路径，那么$(v_i,...,v_1,...v_j)$就有可能是从$v_i$到$v_j$的中间顶点下标序号不大于1的最短路径。

• 将前两步找到的从$v_i$到$v_j$中间顶点下标序号不大于1的最短路径和从 $v_i$到$v_j$中间顶点下标序号不大于0的最短路径进行比较，从中选出$v_i$到$v_j$中间顶点下标序号不大于1的最短路径。

• 再增加一个顶点$v_2$进行试探，以此类推，经过n次之后得到的必是从$v_i到v_j$的最短路径。

参考：《数据结构》（C语言版） 严蔚敏 吴伟民 清华大学出版社