二叉搜索树 C语言实现

1、二叉搜索树基本概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是一棵具有如下特性的非空二叉树：

（1）若它的左子树非空，则左子树上所有结点的关键字均小于根结点的关键字；

（2）若它的右子树非空，则右子树上所有结点的关键字均大于（允许的话，也可大于等于）根结点的关键字；

（3）左右子树本身又各是一个二叉搜索树。

根据二叉搜索树的特点知：对二叉搜索树进行中序遍历得到的结点序列必然是一个有序序列。

2、二叉搜索树的操作

下面通过详细程序展示二叉搜索树的操作

#include<stdio.h>
#include<stdlib.h>
#define QueueMaxSize 20 //定义队列数组长度
#define StackMaxSize 10 //定义栈数组长度
typedef int ElemType;
struct BTreeNode
{
    ElemType data;
    struct BTreeNode* left;
    struct BTreeNode* right;
};

//1、查找等于给定值x的元素，成功返回该结点值域的地址，否则返回NULL
//a、递归方式：（消耗大量时间和空间）
ElemType* Find(struct BTreeNode* BST, ElemType x)
{
    if (BST == NULL)
        return NULL;
    else
    {
        if (x == BST->data) //若结点值等于x则返回结点值域的地址
            return &(BST->data);
        else if (x < BST->data)
            return Find(BST->left, x); //向左子树继续查找并直接返回
        else
            return Find(BST->right, x);//向右子树继续查找并直接返回
    }
}
//b、非递归方式
ElemType* Find1(struct BTreeNode* BST, ElemType x)
{
    while (BST != NULL)
    {
        if (x == BST->data) //若结点值等于x则返回结点值域的地址
            return &(BST->data);
        else if (x < BST->data)
            BST = BST->left;
        else
            BST = BST->right;
    }
    return NULL;
}

//2、更新：与查找算法相同，只需在返回之前先将找到的值替换再返回就行了，在此省略。
//3、向二叉搜索树中插入元素x
//a、递归方式：
void Insert(struct BTreeNode** BST, ElemType x)
{
    if (*BST == NULL) //在为空指针的位置链接新结点
    {
        struct BTreeNode* p = malloc(sizeof(struct BTreeNode));
        p->data = x;
        p->left = p->right = NULL;
        *BST = p;
    }
    else if (x < (*BST)->data) //向左子树中完成插入运算
        Insert(&((*BST)->left), x);
    else
        Insert(&((*BST)->right), x); //向右子树中完成插入运算
}
//b、非递归方式
void Insert1(struct BTreeNode** BST, ElemType x)
{
    struct BTreeNode* p;
    struct BTreeNode* t = *BST, *parent = NULL;
    while (t != NULL) //为插入新元素寻找插入位置
    {
        parent = t;
        if (x < t->data)
            t = t->left;
        else
            t = t->right;
    }//循环之后parent存储的是待插入位置的双亲结点
    p = malloc(sizeof(struct BTreeNode));
    p->data = x;
    p->left = p->right = NULL;
    if (parent == NULL) //若树为空，作为根结点插入
        *BST = p;
    else if (x < parent->data) //链接到左指针域
        parent->left = p;
    else
        parent->right = p; //链接到右指针域
}

//4、删除
//a：删除叶子结点，只要将其双亲结点链接到它的指针置空即可。
//b：删除单支结点，只要将其后继指针链接到它所在的链接位置即可
//c：删除双支结点，一般采用的方法是首先把它的中序前驱结点的值赋给该结点的值域，
//然后再删除它的中序前驱结点，若它的中序前驱结点还是双支结点，继续对其做同样的操作，
//若是叶子结点或单支结点则做对应的操作，若是根结点则结束。
int Delete(struct BTreeNode** BST, ElemType x)
{
    struct BTreeNode* temp;
    temp = *BST;
    if (*BST == NULL)
        return 0;
    if (x < (*BST)->data) //带删除元素小于树根结点值，继续在左子树中删除
        return Delete(&((*BST)->left), x);
    if (x > (*BST)->data) //带删除元素大于树根结点值，继续在右子树中删除
        return Delete(&((*BST)->right), x);
    if ((*BST)->left == NULL)//待删除元素等于树根结点值且左子树为空，将右子树作为整个树并返回1
    {
        *BST = (*BST)->right;
        free(temp);
        return 1;
    }
    else if ((*BST)->right == NULL)//待删除元素等于树根结点值且右子树为空，将左子树作为整个树并返回1
    {
        *BST = (*BST)->left;
        free(temp);
        return 1;
    }
    else//待删除元素等于树根结点值且左右子树均不为空时处理情况
    {
        if ((*BST)->left->right == NULL)//中序前驱结点就是左孩子结点时，把左孩子结点赋值给树根结点
                                        //然后从左子树中删除跟结点
        {
            (*BST)->data = (*BST)->left->data;
            return Delete(&((*BST)->left), (*BST)->data);
        }
        else//查找出中序前驱结点，把该结点值赋给树根结点，然后从中序前驱结点为根结点的树上删除根结点
        {
            struct BTreeNode *p1 = *BST, *p2 = p1->left;
            while (p2->right != NULL)
            {
                p1 = p2;
                p2 = p2->right;
            }
            (*BST)->data = p2->data;
            return Delete(&(p1->right), p2->data);
        }
    }
}

//5、创建二叉搜索树，根据二叉搜索树的插入算法可以很容易实现
void CreateBSTree(struct BTreeNode** BST, ElemType a[], int n)
{
    int i;
    *BST = NULL;
    for (i = 0; i < n; i++)
        Insert1(BST, a[i]);
}

//6、二叉搜索树中可以直接用到二叉树中部分的操作，这里可以用到二叉树的输出、中序遍历和清除函数
//这里只在需要的地方将其元素类型换为int，函数名后加上_int后缀，用来区分
//输出二叉树，可在前序遍历的基础上修改。采用广义表格式，元素类型为int
void PrintBTree_int(struct BTreeNode* BT)
{
    if (BT != NULL)
    {
        printf("%d", BT->data); //输出根结点的值
        if (BT->left != NULL || BT->right != NULL)
        {
            printf("(");
            PrintBTree_int(BT->left); //输出左子树
            if (BT->right != NULL)
                printf(",");
            PrintBTree_int(BT->right); //输出右子树
            printf(")");
        }
    }
}
void Inorder_int(struct BTreeNode* BT)//中序遍历,元素类型为int
{
    if (BT != NULL)
    {
        Inorder_int(BT->left);
        printf("%d,", BT->data);
        Inorder_int(BT->right);
    }
}
void ClearBTree(struct BTreeNode** BT)//清除二叉树，使之变为一棵空树
{
    if (*BT != NULL)
    {
        ClearBTree(&((*BT)->left));//删除左子树
        ClearBTree(&((*BT)->right));//删除右子树
        free(*BT);            //释放根结点
        *BT = NULL;           //置根指针为空
    }
}

//主函数
void main()//其中用到二叉树操作的函数都基本没变，只是元素类型换为int
{
    int x, *px;
    ElemType a[10] = {30,50,20,40,25,70,54,23,80,92};
    struct BTreeNode* bst = NULL;
    CreateBSTree(&bst, a, 10); //利用数组a建立一棵树根指针为bst的二叉搜索树
    printf("建立的二叉搜索树的广义表形式为：\n");
    PrintBTree_int(bst);
    printf("\n");

    printf("中序遍历：\n");
    Inorder_int(bst);
    printf("\n");

    printf("输入待查找元素值：");
    scanf(" %d", &x);//格式串中的空格可以跳过任何空白符
    if (px = Find(bst, x))
        printf("查找成功！得到的x为：%d\n", *px);
    else
        printf("查找失败！\n");

    printf("输入待插入元素值：");
    scanf(" %d", &x);
    Insert(&bst, x);

    printf("输入待插入元素值：");
    scanf(" %d", &x);
    Insert(&bst, x);

    printf("输入待插入元素值：");
    scanf(" %d", &x);
    Insert(&bst, x);

    printf("进行相应操作后的中序遍历为：\n");
    Inorder_int(bst);
    printf("\n");

    printf("输入待删除元素值：");
    scanf(" %d", &x);
    if (Delete(&bst, x))
        printf("1\n");
    else
        printf("0\n");

    printf("进行相应操作后的中序遍历为：\n");
    Inorder_int(bst);
    printf("\n");

    printf("操作后的二叉搜索树的广义表形式为：\n");
    PrintBTree_int(bst);
    printf("\n");

    ClearBTree(&bst);
}

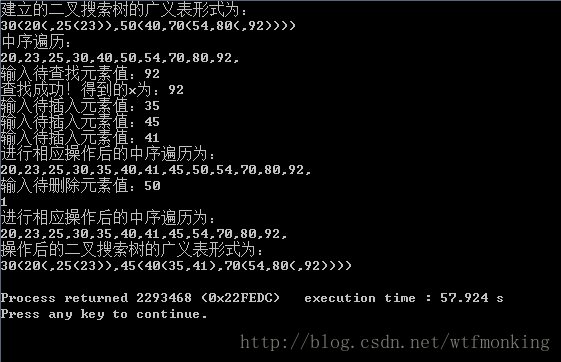
运行结果：

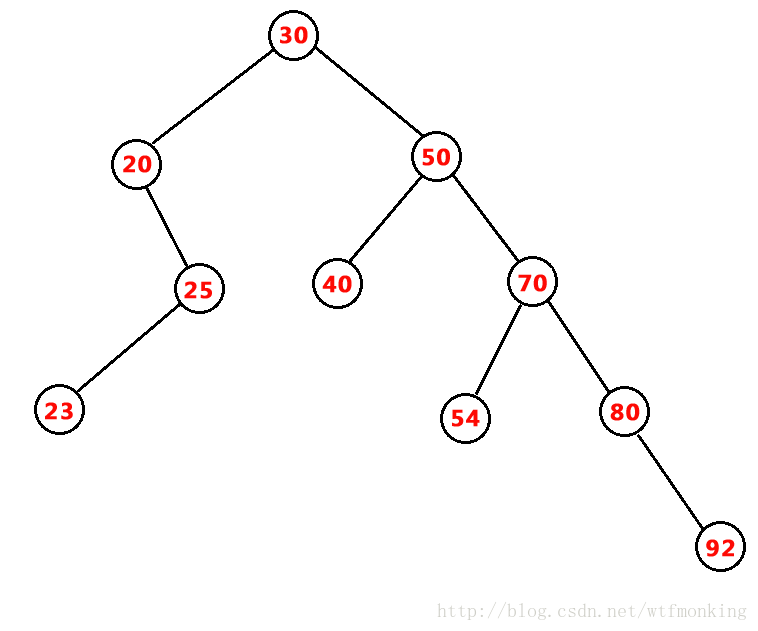
分析：此程序的初始二叉搜索树如下：

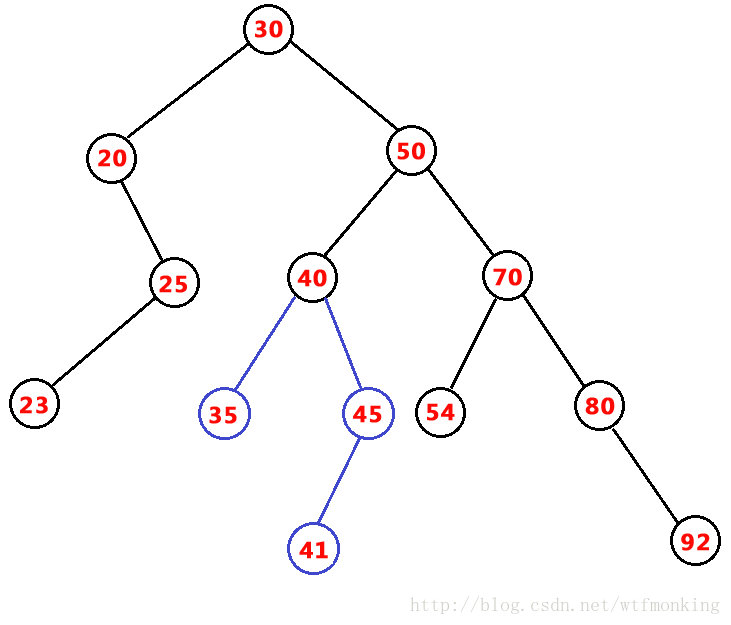
然后依次插入：35,45,41 三个元素，插入后的二叉搜索树如下：

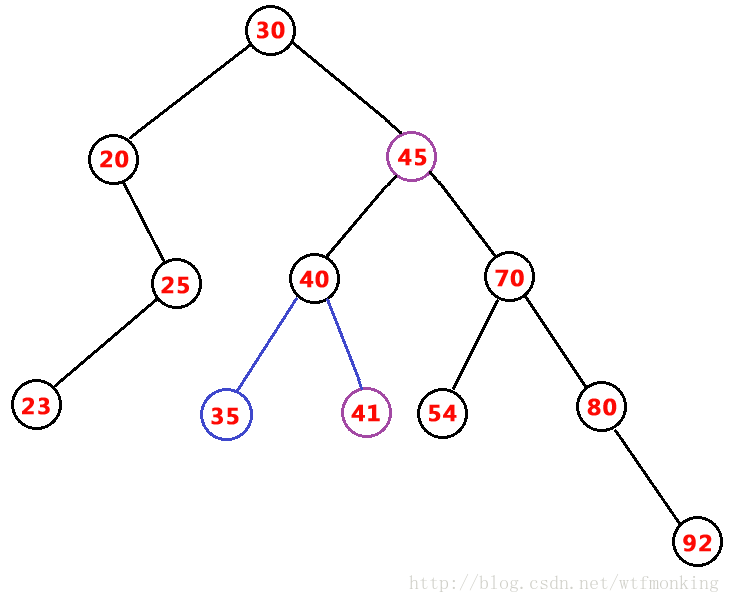
最后删除元素为50的结点，删除结点后的二叉搜索树如下：

删除结点前的中序遍历为：20,23,25,30,35,40,41,45,50,54,70,80,92

删除过程：

   需要删除的结点是：元素为50的结点，此结点为双支结点，我们知道其中序前驱结点（中序序列中处于它前面的一个结点）为45，所以将45替换到50的位置，

   而45结点有一个左孩子，45结点为单支结点，则直接将其后续结点（此处为左孩子41）替换原45结点的位置。删除完成。