hdu5476Explore Track of Point+平面几何

Problem Description
In Geometry, the problem of track is very interesting. Because in some cases, the track of point may be beautiful curve. For example, in polar Coordinate system, ρ=cos3θ is like rose, ρ=1−sinθ is a Cardioid, and so on. Today, there is a simple problem about it which you need to solve.

Give you a triangle ΔABC and AB = AC. M is the midpoint of BC. Point P is in ΔABC and makes min{∠MPB+∠APC,∠MPC+∠APB} maximum. The track of P is Γ. Would you mind calculating the length of Γ?

Given the coordinate of A, B, C, please output the length of Γ.

Input
There are T (1≤T≤104) test cases. For each case, one line includes six integers the coordinate of A, B, C in order. It is guaranteed that AB = AC and three points are not collinear. All coordinates do not exceed 104 by absolute value.

Output
For each case, first please output “Case #k: “, k is the number of test case. See sample output for more detail. Then, please output the length of Γ with exactly 4 digits after the decimal point.

Sample Input

1
0 1 -1 0 1 0

Sample Output

Case #1: 3.2214

Source
2015 ACM/ICPC Asia Regional Shanghai Online
盗了一张图。

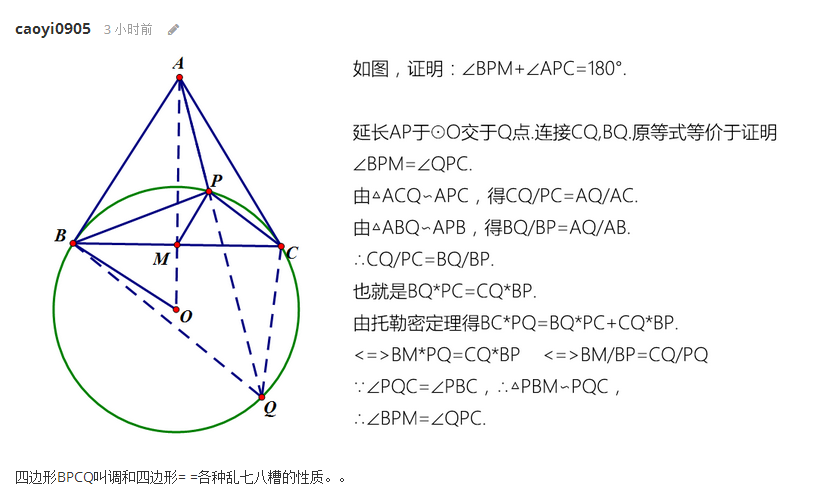
答案就是劣弧BC+AM
由相似的r.

#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<queue>
#include<vector>
#include<map>
#include<stack>
#include<set>
#define pi acos(-1.0)
#define EPS 1e-6    //log(x)
#define e exp(1.0); //2.718281828
#define mod 1000000007
#define INF 0x7fffffff
#define inf 0x3f3f3f3f
typedef long long LL;
using namespace std;
double dis(double x1,double y1,double x2,double y2){
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
int main()
{
    int t;
    scanf("%d",&t);
    double ax,ay,bx,by,cx,cy;
    for(int cas=1;cas<=t;cas++){
        scanf("%lf %lf %lf %lf %lf %lf",&ax,&ay,&bx,&by,&cx,&cy);
        double mx=(bx+cx)/2,my=(by+cy)/2;
        double am=dis(ax,ay,mx,my);
        double bm=dis(bx,by,mx,my);
        double ab=dis(ax,ay,bx,by);
        double r=ab*bm/am;
        //cout<<r<<" "<<bm<<endl;
        //cout<<acos(bm/r)<<endl;
        double ans=(pi/2-acos(bm/r))*2*r;
        printf("Case #%d: %.4f\n",cas,ans+am);
    }

    return 0;
}

/*
                   _ooOoo_
                  o8888888o
                  88" . "88
                  (| -_- |)
                  O\  =  /O
               ____/`---'\____
             .'  \\|     |//  `.
            /  \\|||  :  |||//  \
           /  _||||| -:- |||||-  \
           |   | \\\  -  /// |   |
           | \_|  ''\---/''  |   |
           \  .-\__  `-`  ___/-. /
         ___`. .'  /--.--\  `. . __
      ."" '<  `.___\_<|>_/___.'  >'"".
     | | :  `- \`.;`\ _ /`;.`/ - ` : | |
     \  \ `-.   \_ __\ /__ _/   .-` /  /
======`-.____`-.___\_____/___.-`____.-'======
                   `=---='
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
         I have a dream!A AC deram!!
 orz orz orz orz orz orz orz orz orz orz orz
 orz orz orz orz orz orz orz orz orz orz orz
 orz orz orz orz orz orz orz orz orz orz orz

*/