SAS主成分分析

同事讲主成分分析，举了这么个例子：就像你选女人，有身材、相貌两个指标，如果身材、相貌都很突出，那当然很好选择；但如果两个女人，一个身材突出，一个相貌出众，看着都很喜欢，那可如何是好！这个时候通过主成分分析，汇总出一个指标，这个指标可以一定程度上代替原来的身材、相貌，这时就可以排序做出选择了。

这例子当然有很多缺陷，但至少指出了主成分分析的目的之一：减少决策变量数，也就是降维。主成分分析的另一个目的是防范多重共线性。实际问题往往涉及很多变量，但某些变量之间会有一定的相关性，我们希望构造较少的几个互不相关的新指标来代替原始变量，去除多重共线性，减少所需分析的变量，同时尽可能减少这一过程的信息损失。主成分分析正是基于这样的目的而产生的有效方法。

主成分分析流程

主成分分析包含以下流程：

1、原始数据标准化。

2、计算标准化变量间的相关系数矩阵。

3、计算相关系数矩阵的特征值和特征向量。

4、计算主成分变量值。

5、统计结果分析，提取所需的主成分。

SAS主成分分析示例

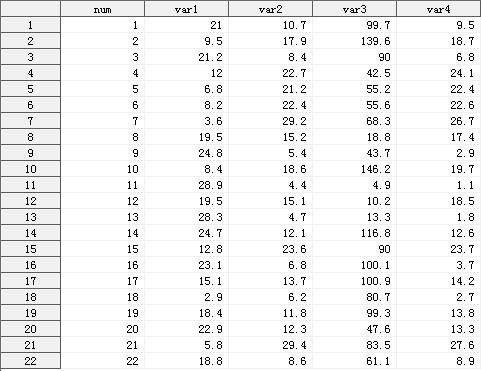
我们从实战入手，先来个简单的例子，完整体验使用SAS进行主成分分析的过程。 准备好图1所示的数据集，该数据集包含5个变量和22个观测。其中变量num用于标识每条观测。

图1

可以直接复制下面的程序完成输入：

data  Practice.PCA_Demo;

            input  num var1 var2 var3 var4;

            cards ;

          1        21      10.7   99.7   9.5

          2        9.5     17.9   139.6  18.7

          3        21.2   8.4     90      6.8

          4        12      22.7   42.5   24.1

          5        6.8     21.2   55.2   22.4

          6        8.2     22.4   55.6   22.6

          7        3.6     29.2   68.3   26.7

          8        19.5   15.2   18.8   17.4

          9        24.8   5.4     43.7   2.9

          10      8.4     18.6   146.2  19.7

          11      28.9   4.4     4.9     1.1

          12      19.5   15.1   10.2   18.5

          13      28.3   4.7     13.3   1.8

          14      24.7   12.1   116.8  12.6

          15      12.8   23.6   90      23.7

          16      23.1   6.8     100.1  3.7

          17      15.1   13.7   100.9  14.2

          18      2.9     6.2     80.7   2.7

          19      18.4   11.8   99.3   13.8

          20      22.9   12.3   47.6   13.3

          21      5.8     29.4   83.5   27.6

          22      18.8   8.6     61.1   8.9

;

run  ;

我们的目的是，化简var1-var4四个变量，找出可以替代这四个变量的若干个彼此独立的新变量，也就是找出主成分。主成分分析代码如下：

proc  princomp

            data  = Practice.PCA_Demo

            out  = Work.PCA_Demo_out

            prefix  = comp

            outstat  = Work.PCA_Demo_stat

          ;

            var  var1 var2 var3 var4;

run  ;

这段代码翻译过来的意思是：对源数据Practice.PCA_Demo的四个变量var1、var2、var3和var4（以下简称原始变量）做主成分分析，输出结果（包含源数据的所有变量及新增的主成分变量）放在Work.PCA_Demo_out数据集，主成分变量名的前缀使用comp。相关变量的统计结果（均值、方差、特征值、特征向量等）输出到Work.PCA_Demo_stat。

程序运行后，输出界面显示如图2。

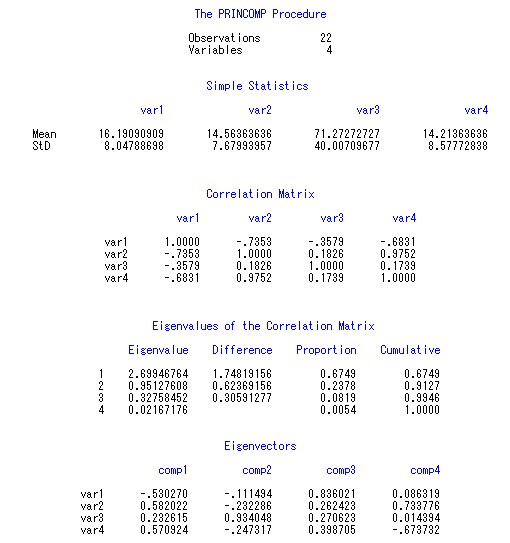
图2

输出结果Work.PCA_Demo_out存放了原始数据集的所有变量以及新变量comp1、comp2、comp3和comp4，分别代表第1至第4主成分，它们对原始变量的解释力度依次减少。

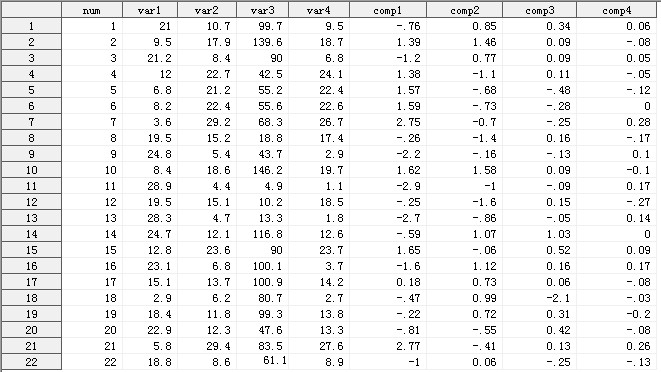
图3

一同输出的还有统计结果Work.PCA_Demo_stat：

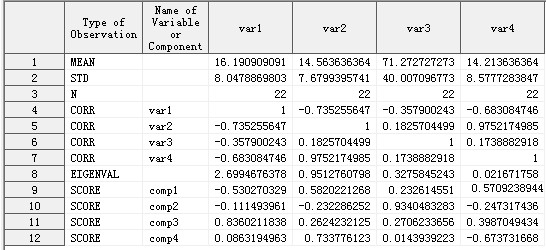
图4

现在，我先假设你是个急性子，你可能会对我说：“不必告诉我这些输出结果的含义，我给了你四个变量，你只要返回给我较少的可用的字段就可以了。”那么我会回答你，新的变量comp1和comp2就可以替代原来的四个变量var1、var2、var3和var4，因为这两个变量合起来解释了原来四个变量91.27%的信息，能够满足要求。

何以见得？请看图2的第4部分输出Eigenvalues of the Correlation Matrix，第四列Cumulative显示，第一个特征值分量占比0.6749（67.49%），第1、2个特征值合起来占比91.27%>85%，因此新变量comp1和comp2已经足以替代原有四个变量，它们是源数据集的主成分。

没错，在SAS上进行主成分分析，就是这么简单，结果的使用也不复杂，大多数情况下到此也就足够了。不过出于对科学本质的好奇，我们还是要详细研究下每项输出结果的含义，以便更好地理解主成分分析。

SAS主成分分析输出结果详解

作为细节强迫症重度患者，图2~图4只要有个点没搞清楚都觉得寝食难安。

我们先来看图2。

第1部分很简单，指出观测数为22，变量数为4，也就是我们在var语句中指定4个原始变量。

第2部分Simple Statistics是对原始变量的简单描述性统计，Mean是均值，StD是标准偏差（注意标准偏差与标准差的区别）。

Mean的计算公式我们都很熟悉，就是

（1）

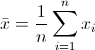
标准偏差StD的计算公式是：

（2）

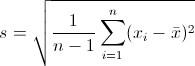
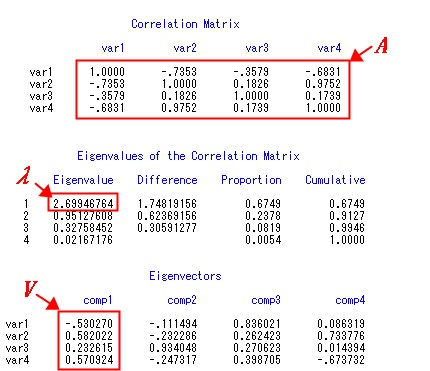
第3部分Correlation Matrix是原始变量的相关系数矩阵，其中的元素代表4个原始变量两两之间的相关系数。

相关系数的计算公式是：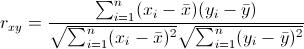

（3）

从原始变量的相关系数矩阵可以看出，变量var1和var2、var1和var4呈现出较为显著的负相关，变量var2和var4则是强烈的正相关，其相关系数高达0.9752。

第4部分Eigenvalues of the Correlation Matrix输出了相关系数矩阵的特征值。Eigenvalue一列从大到小依次展示了4个特征值，特征值越大，表示对应的主成分变量包含的信息越多，对原始变量的解释力度越强。
Difference是相邻两个特征值的差，比如1.74819156 = 2.69946764 - 0.95127608。
Proportion表示主成分的贡献率，也就是，比如第1个特征值的贡献率0.6749 = 2.69946764 / (2.69946764+0.95127608+0.32758452+0.02167176)。
Cumulative则是累计贡献率，到第2个特征值累计贡献率0.9127 = 0.6749 + 0.2378。
我们在判断应提取多少个主成分时，根据的就是累计贡献率。0.9127的累计贡献率说明特征值1和特征值2对应的主成分变量comp1和comp2合起来能够反映原始变量91.27%的信息，能够满足应用需求。这时我们可以作出决策：提取两个主成分comp1和comp2代替4个原始变量。而如果我们希望主成分变量对原始变量的解释力度应达到95%以上，那么就需要加入comp3，共提取3个主成分，其累计贡献率达到99.46%。而提取全部4个主成分变量，则没有达到降维的目的，意义已经不大。至于这个累计贡献率要达到多少才算满足需求，需要视具体业务需求而定，我们的参考值是85%。

第5部分Eigenvectors是特征值对应的特征向量。图5一秒钟告诉你特征值和特征向量如何对应。图中的第1个特征值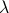=2.699467638对应第一个特征向量V=(-0.530270329, 0.582022127, 0.232614551, 0.570923894)。同理可知第2个特征值和第2个特征向量的对应。

图5

特征值和特征向量的计算，依据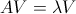的公式。这里A是相关系数矩阵（见图5）。

可以自行验证下面的等式是成立的。

若要自行计算特征值和特征向量，可以在proc iml过程步中调用eigen。上面计算相关系数矩阵的特征值和特征向量代码如下：

proc  iml ;

          A={  1  -  0.735255647  -  0.357900243  -  0.683084746  ,

          -  0.735255647   1   0.18257045   0.975217499  ,

          -  0.357900243   0.18257045   1   0.173888292  ,

          -  0.683084746   0.975217499   0.173888292   1

          };

            call  eigen(eigenvalues, eigenvectors, A);

            print  A eigenvalues eigenvectors;

quit  ;

现在，我们要解读图3，根据前面的分析，在图3的数据集Work.PCA_Demo_out中，我们只要保留num、comp1和comp2三个字段，所形成的新数据集就可以替代源数据集，供未来的分析所使用。

接下来，我们要来回答：主成分变量comp1、comp2、comp3和comp4的值是怎么来的？

我们知道，主成分变量是原始变量的线性表示，用公式表示如下：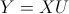

（4）

其中，X表示原始变量对应数据组成的矩阵（以下称为原始数据矩阵），U是特征向量以列向量形式依次排列组成的矩阵（以下称为特征向量矩阵）。在我们的示例中，

那么公式（4）的计算结果是：

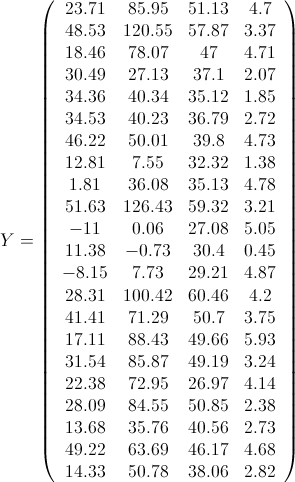
什么？跟实际输出结果不符？挺好的，掉一次坑你就印象深刻了。事实上主成分数据矩阵不是原始数据矩阵和特征向量矩阵直接相乘的结果，而是原始数据标准化后的数据矩阵和特征向量矩阵相乘的结果。这就回到我们在主成分分析流程就已经提到的至关重要的第一步：原始数据标准化！数据标准化使得变量的平均值为0，标准偏差为1，消除了不同量纲对分析过程的影响。

图3的输出结果是有缺失的，我们看不到原始变量的标准化变量。我们可以使用proc standard过程步来查看数据标准化的结果，代码如下：

proc  standard

            data  = Practice.PCA_Demo

            out  = Work.PCA_Demo_std

            mean  =  0

            std = 1 ;

            var  var1 var2 var3 var4;

run  ;

打开输出数据集Work.PCA_Demo_std，就能看到转化结果：

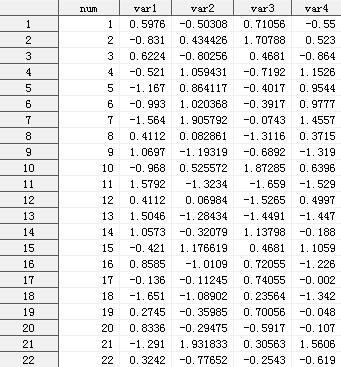
图6

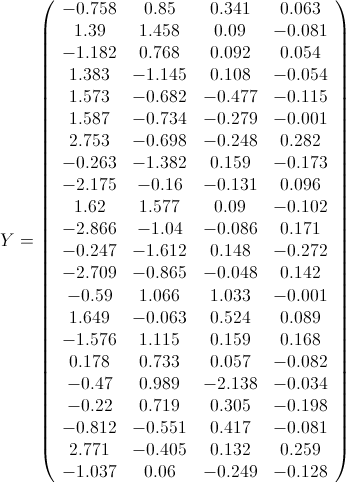
现在，我们来修正下公式（4）

（5）

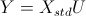
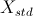
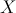
其中，是的数据标准化后的矩阵

现在再计算一遍Y，看看是不是如下结果呢？

矩阵的乘法公式告诉我们，本质上，某一个样本（比如样本1：(1, 21, 10.7, 99.7,9.5)）的第一主成分变量的值（-0.75812），就是原始变量标准化后组成的行向量（0.598, -0.503, 0.711, -0.55）与第一特征向量（列向量）（-0.530270329; 0.582022127; 0.232614551; 0.570923894）的乘积。第二主成分变量值，是原始变量组成的行向量与第二特征向量（列向量）的乘积。依次类推。

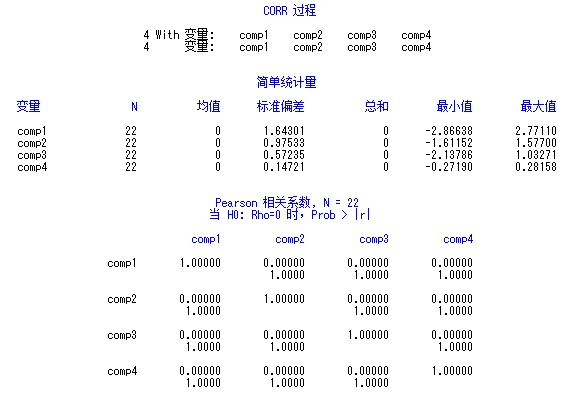
我们来验证一下主成分变量之间是否线性无关。使用proc corr过程步可以计算变量之间的相关系数，代码如下：

proc  corr

            data  = Work.PCA_Demo_out

          out = Work.PCA_Demo_Comp_Corr

          ;

            var  comp1-comp4;

            with  comp1-comp4;

run  ;

输出结果为：

图7

可以看出，主成分变量之间的相关系数都为零。

最后我们来说说图4的统计结果Work.PCA_Demo_stat，它其实就是把图2的输出结果存入数据集中。
从表中Type of Observation字段可以看出，MEAN表示均值，STD是标准偏差，N是观测数，CORR是相关系数，EIGENVAL是特征值，SCORE是以行向量形式表示的特征向量。

特征值和特征向量隐藏的秘密

主成分变量对应的特征向量的每个元素，与对应的特征值的平方根的乘积，等于该主成分变量，与该元素列标签对应的原始变量之间的相关系数。这是特征值与特征向量隐藏的秘密，可以用矩阵代数严格推导出来。不过这句话读起来比较费劲，我们用图8来表示这一关系。图中的eigVec1至eigVec4是4个特征向量，对应的特征值分别为eigVal1至eigVal4。我们在每个列中进行操作，用特征向量每个元素分别乘以对应特征值的平方根，得到该主成分变量与所有原始变量的相关系数。

图8

同样的，可以使用proc corr过程计算相关系数，代码如下：

proc  corr

            data  = Work.PCA_Demo_out

          out = Work.PCA_Demo_Corr

          ;

            var  comp1-comp4;

            with  var1-var4;

run  ;

输出结果为：

图9

输出结果的第一行表示相关系数的值，第二行表示零假设下的检验概率。 这些相关系数有其统计学名字，称为因子载荷量，反映了主成分变量受原始变量影响的程度，其绝对值越大，表示该主成分受该原始变量的影响越大，而值的符号则表示影响的方向。比如，comp1和var1的相关系数为-0.8712，检验概率<0.0001，在0.1水平上显著。

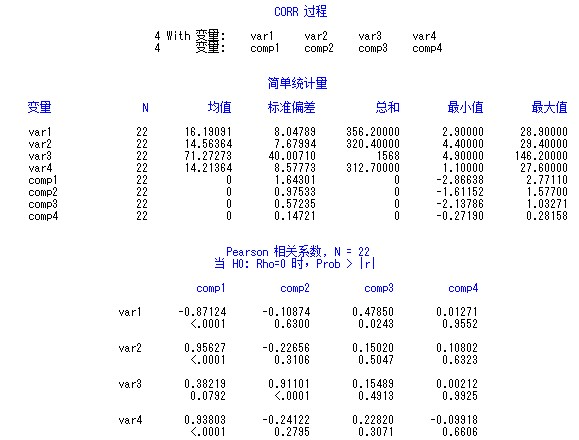
总结

以下概念很容易混淆，值得拎出来做一梳理：
原始变量之间的相关系数矩阵：可以看出原始变量之间的相关性。
原始变量和主成分变量之间的相关系数矩阵：可以看出主成分变量受原始变量影响的程度。
主成分变量之间的相关系数矩阵：主成分变量之间相关系数为零。
特征值：原始变量相关系数矩阵的特征值。
特征向量：原始变量相关系数矩阵的特征向量。

参考文献：

[1] 黄燕，吴平编著. 《SAS统计分析及应用》，机械工业出版社。

[2] SAS帮助和文档。