FFT，快速傅里叶变换学习笔记

FFT，快速傅里叶变换

描述问题

计算两个n阶多项式的加法，需要$\Theta(n)$的时间。只需要将两式对应次数的系数相加即可。但是两个n阶多项式A、B相乘需要$\Theta(n^2)$的时间，因为我们需要将A式的每一个系数乘上B式中每一个系数，在找次数相同的系数进行合并。我们希望加速多项式相乘的过程。

多项式有两种表示法，系数表示法与点值表示法。系数表示法表示一个多项式A可以记为：

$$A(x)=\sum_{i=0}^{n-1}{a_ix^j}$$
点值法表示多项式B可以记为：
$$\{\ (x_0,B(x_0)),(x_1,B(x_1))...(x_{n-1},B(x_{n-1}))\ \}$$
可以证明，一个包含n个点的点值表示法可以唯一确定一个n-1次多项式(最高项次数为n-1)。

点值表示法得优势在于：对于点值表示的多项式，相加相乘都很方便，我们只需要将同一x对应的y相乘，就得到新多项式的点值表示。注意，因为两个n次多项式的乘积是2n次，所以我们在选点时要选2n个点。这样乘起来才会得到2n个点。所以我们快速做多项式乘法的思路就是先将系数表示的多项式转化成点值表示，相乘，在转化回系数表示。

但是一般而言，对于系数表示法的多项式A，我们要求出2n个点，需要$\Theta(n^2)$的时间。因为我们求一个x对应的$A(x)$需要$\Theta(n)$的时间，$A(x_0)=a_0+x_0(a_1+x_0(a_2+...+x_0(a_{n-2}+x_0(a_{n-1}))))$。但是如果我们选取2n次单位复数根，并利用单位复数根单位性质进行分治，就可以将复杂度降至$\Theta(nlogn)$。

算法

DFT

在DFT变换中, 希望计算多项式A(x)在复数根$\omega_n^0, \omega_n^1, ..., \omega_n^{n - 1}$处的值, 也就是求：

$$y_k = A(\omega_n^k) = \mathop{\Sigma}_{j = 0}^{n - 1}a_j\omega_n^{kj}$$
称向量 $y = (y_0, y_1, ..., y_{n - 1})$是系数向量 $a = (a_0, a_1, ..., a_{n - 1})$的离散傅里叶变换, 记为 $y = DFT_n(a)$。
$$y_k = A(\omega_n^k) = \mathop{\Sigma}_{j = 0}^{n - 1}a_j\omega_n^{kj}$$
称向量 $y = (y_0, y_1, ..., y_{n - 1})$为系数向量的离散傅里叶变换，记为 $y=DFT_n(s)$ 。

FFT

直接计算DFT的复杂度仍是$\Theta(n^2)$，但是我们利用消去引理的一个推论：$\omega_n^{n/2}=\omega_2=-1$，结合分治的策略，可以将复杂度降为$\Theta(nlogn)$。

我们假定n为2的整次幂，若不是，在前面填0补足即可。每一步将当前的多项式A(x), 次数是2的倍数, 分成两个部分：

$$A^{[0]}(x) = a_0 + a_2x + a_4x^2 + ... + a_{n - 2}x^{\frac{n}{2} - 1}$$

$$A^{[1]}(x) = a_1 + a_3x^1 + a_5x^2 + ... + a_{n - 1}x^{\frac{n}{2} - 1}$$

于是就有了：

$$A(x) = A^{[0]}(x^2) + xA^{[1]}(x^2)$$
那么我们如果能求出次数界是 $\frac{n}{2}$的多项式 $A^{[0]}(x)$和 $A^{[1]}(x)$在n个n次单位复数根的平方处的取值就可以了, 即在：
$$(\omega_n^0)^2, (\omega_n^1)^2, (\omega_n^2)^2, ...,(\omega_n^{n - 1})^2$$
处的值。

折半引理：

$$\omega_n^{k+n/2}=\omega_n^k*\omega_n^{n/2}=-\omega_n^{n/2}$$

根据折半引理，这n个数其实只有$\frac{n}{2}$个不同的值，因为相反数平方后相等。也就是说，对于每次分出的两个次数界$\frac{n}{2}$的多项式, 只需要求出其$\frac{n}{2}$个不同的值即可，那么问题就递归到了原来规模的一半。我们根据这个式子可以得到一个递归的实现。

RECURSIVE_FFT(a[])
{
  n=a.lenth
  if(n==1) return a
  wn=e^(2*pi*i/n)
  w=1
  a0[]=(a0,a2,a4...)
  a1[]=(a1,a3,a5...)
  y0[]=RECURSIVE_FFT(a0[])
  y1[]=RECURSIVE_FFT(a1[])
  for k=0 to n/2-1
    y[k]=y0[k]+w*y1[k]
    y[k+n/2]=y0[k]-w*y1[k]
    w=w*wn
  return y
}

FFT算法复杂度

因为我们将n扩展为了2的整次幂，所以每次递归子问题是原来问题规模的一半。

$$T(n)=2T(\frac{n}{2})+\Theta(n)=\Theta(nlogn)$$

FFT算法的实现

递归版本的FFT实现：

typedef complex<double> Complex;
const double pi=acos(-1.0);
vector<Complex> recursive_fft(vector<Complex> a,int oper)
{
    int n=a.size();
    if(n==1)
    {
        return a;
    }
    Complex omgn;
    omgn=Complex(cos(2*pi/n*oper), sin(2*pi/n*oper));
    Complex omg=Complex(1, 0);
    vector<Complex> a0, a1;
    for(int i=0;i<n;i++)
    {
        if(i%2) a1.push_back(a[i]);
        else a0.push_back(a[i]);
    }
    vector<Complex> y0=recursive_fft(a0, oper);
    vector<Complex> y1=recursive_fft(a1, oper);
    vector<Complex> y;y.resize(n);
    for(int k=0;k<n/2;k++)
    {
        Complex tmp=omg*y1[k];
        y[k]=y0[k]+tmp;
        y[k+n/2]=y0[k]-tmp;
        omg=omg*omgn;
    }
    return y;
}

调用之前保证vector a的size已经被置为2的整数次幂。

算法改进

时间复杂度基本不能优化，空间复杂度可以。不采用递归，而采用迭代实现，可以避免重复开数组。

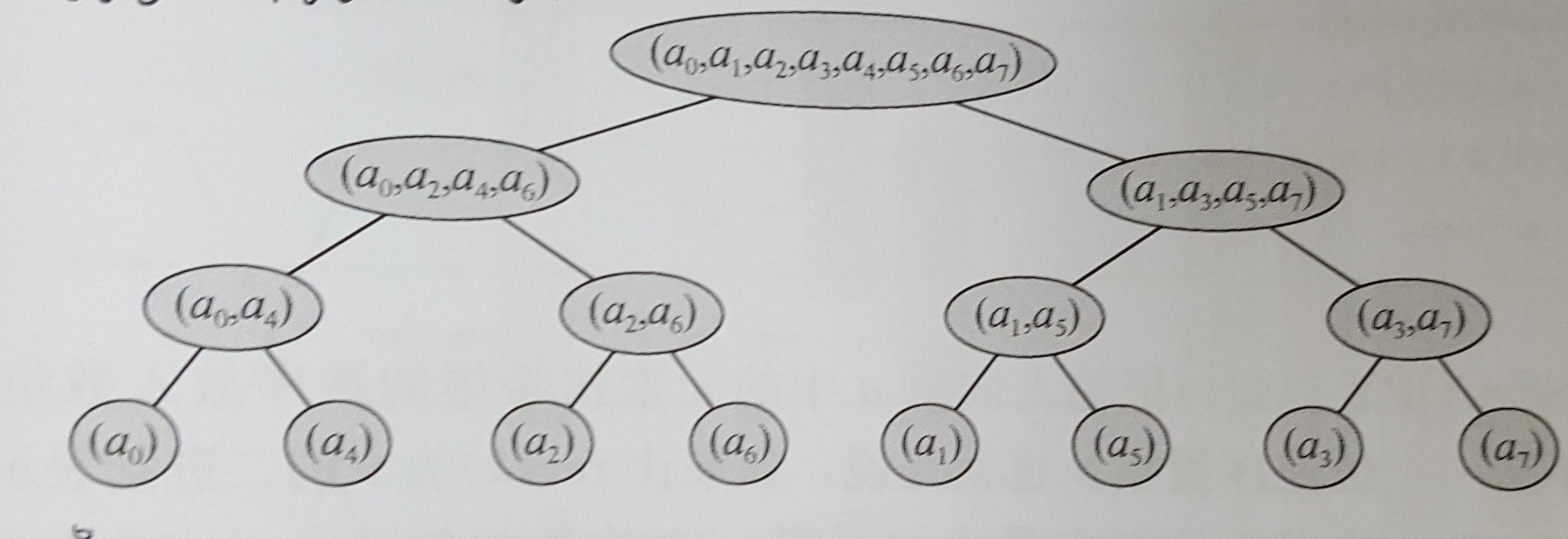
首先，观察a数组的递归调用树，可以发现

可以事先将a数组排序成这种形式，然后从底层算起，每算完一层就提高一层，每层中计算$2^{层数}$个。

迭代版FFT

int bit_reverst(int n, int ma)
{
    int res=0;
    ma--;
    while(ma)
    {
        res|=(n&1);
        res<<=1;
        n>>=1;
        ma>>=1;
    }
    res>>=1;
    return res;
}
void bit_reverse_copy(vector<Complex> &a, vector<Complex> &A)
{
    int n=a.size();
    A.resize(n);
    for(int k=0;k<n;k++)
    {
        int revk=bit_reverst(k, n);
        A[revk]=a[k];
    }
}
vector<Complex> iterative_fft(vector<Complex> &a, int oper)
{
    vector<Complex> A;
    bit_reverse_copy(a, A);
    int n=a.size();

    for(int s=0; (1<<s)<n; s++)
    {
        int m=1<<s, m2=m*2;
        Complex omgm=Complex(cos(pi/m*oper), sin(pi/m*oper));
        for(int k=0;k<n;k+=m2)
        {
            Complex omg=Complex(1, 0);
            for(int j=0;j<m;j++)
            {
                Complex t=omg*A[k+j+m];
                Complex u=A[k+j];
                A[k+j]=u+t;
                A[k+j+m]=u-t;
                omg=omg*omgm;
            }
        }
    }
    return A;
}

bit_reverst函数是将一个数进行二进制位的反转，比如6=110，rev(6)=011=3。

bit_reverse_copy函数将系数数组拷贝并重排序成我们需要的顺序。

iterative_fft实现了一个迭代版本的FFT算法。

迭代版FFT复杂度

s层for循环执行了logn次，k层for循环执行了n/m2=n/(2*m)次，j层for循环执行了m次。总复杂度：

$$logn*\frac{n}{2*m}*m=\Theta{(nlogn)}$$

完整代码

#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <iomanip>
#include <complex>
using namespace std;

const int MAXN=2000000+7;
typedef complex<double> Complex;
const double pi=acos(-1.0);

vector<Complex> recursive_fft(vector<Complex> a,int oper)
{
    int n=a.size();
    if(n==1)
    {
        return a;
    }
    Complex omgn;
    omgn=Complex(cos(2*pi/n*oper), sin(2*pi/n*oper));
    Complex omg=Complex(1, 0);
    vector<Complex> a0, a1;
    for(int i=0;i<n;i++)
    {
        if(i%2) a1.push_back(a[i]);
        else a0.push_back(a[i]);
    }
    vector<Complex> y0=recursive_fft(a0, oper);
    vector<Complex> y1=recursive_fft(a1, oper);
    vector<Complex> y;y.resize(n);
    for(int k=0;k<n/2;k++)
    {
        Complex tmp=omg*y1[k];
        y[k]=y0[k]+tmp;
        y[k+n/2]=y0[k]-tmp;
        omg=omg*omgn;
    }
    return y;
}
int bit_reverst(int n, int ma)
{
    int res=0;
    ma--;
    while(ma)
    {
        res|=(n&1);
        res<<=1;
        n>>=1;
        ma>>=1;
    }
    res>>=1;
    return res;
}
void bit_reverse_copy(vector<Complex> &a, vector<Complex> &A)
{
    int n=a.size();
    A.resize(n);
    for(int k=0;k<n;k++)
    {
        int revk=bit_reverst(k, n);
        A[revk]=a[k];
    }
}
vector<Complex> iterative_fft(vector<Complex> &a, int oper)
{
    vector<Complex> A;
    bit_reverse_copy(a, A);
    int n=a.size();

    for(int s=0; (1<<s)<n; s++)
    {
        int m=1<<s, m2=m*2;
        Complex omgm=Complex(cos(pi/m*oper), sin(pi/m*oper));
        for(int k=0;k<n;k+=m2)
        {
            Complex omg=Complex(1, 0);
            for(int j=0;j<m;j++)
            {
                Complex t=omg*A[k+j+m];
                Complex u=A[k+j];
                A[k+j]=u+t;
                A[k+j+m]=u-t;
                omg=omg*omgm;
            }
        }
    }
    return A;
}


int main()
{
    int n;
    vector<Complex> xs1;
    vector<Complex> xs2;
    while(cin>>n)
    {
        for(int i=0;i<n;i++)
        {
            int tmp;cin>>tmp;
            xs1.push_back(Complex(tmp, 0));
        }
        for(int i=0;i<n;i++)
        {
            int tmp;cin>>tmp;
            xs2.push_back(Complex(tmp, 0));
        }

        vector<Complex> res1;
        vector<Complex> res2;
        vector<Complex> res3;
        res1.resize(n*2);res2.resize(n*2);res3.resize(n*2);
        xs1.resize(n*2);xs2.resize(2*n);
        res1=iterative_fft(xs1, 1);
        res2=iterative_fft(xs2, 1);
        for(int i=0;i<res1.size();i++)
        {
            res3[i]=res1[i]*res2[i];
        }
        vector<Complex> res;res.resize(n*2);
        res=iterative_fft(res3, -1);

        for(int i=0;i<res.size();i++)
        {
            cout<<res[i].real()/n/2<<endl;
        }



        res1=recursive_fft(xs1, 1);
        res2=recursive_fft(xs2, 1);
        for(int i=0;i<res1.size();i++)
        {
            res3[i]=res1[i]*res2[i];
        }
        res=recursive_fft(res3, -1);

        for(int i=0;i<res.size();i++)
        {
            cout<<res[i].real()/n/2<<endl;
        }


    }
    return 0;
}